Histoire des notations mathématiques
L'histoire des notations mathématiques[1] décrit les débuts, les progrès et la diffusion culturelle des symboles mathématiques et les conflits entre méthodes de notation qui ont mené à leur généralisation ou leur marginalisation. La notation mathématique[2] comprend les symboles utilisés pour écrire des équations et formules mathématiques. La notation implique généralement un ensemble de représentations bien définies de quantités et d'opérateurs symboliques[3]. L'histoire inclut les nombres indo-arabes, lettres des alphabets latin, grec, hébreu et gothique, ainsi qu'un ensemble de symboles inventés par les mathématiciens au cours des siècles.
Le développement des notations mathématiques peut être divisé en étapes[4] - [5]. L'étape rhétorique correspond à l'époque où les calculs sont réalisés par des mots, sans symboles[6]. L'étape syncopée en vient à utiliser des abréviations syntaxiques pour les opérations et quantités fréquemment utilisées. De l'Antiquité jusqu'à l'ère post-classique[note 1] des éclats de créativité mathématique ont souvent été suivis par des siècles de stagnation. Au début de l'époque moderne et que l'accès à la connaissance s'est facilité, des exemples écrits de développements mathématiques sont apparus. L'étape symbolique est atteinte quand des systèmes compréhensibles de notation l'emportent sur la rhétorique. Commençant en Italie au XVIe siècle, de nouveaux développements mathématiques, en interaction avec de nouvelles découvertes scientifiques, sont faits à vitesse croissante qui continue encore de nos jours. Cette étape symbolique était déjà d'actualité chez les mathématiciens indiens médiévaux et en Europe depuis le milieu du XVIIe siècle[7] et a continué de se développer à l'époque contemporaine.
Le domaine d'étude connu comme l'histoire des mathématiques est avant tout une investigation des origines des découvertes en mathématiques et, ce qui constitue le sujet de cet article, une étude des méthodes mathématiques et des notations du passé.
Étape rhétorique
Bien que l'histoire commence avec celle des écoles ioniennes, il est établi que ces Grecs anciens qui s'y sont intéressés ont largement bénéficié des travaux précédents des Égyptiens et des Phéniciens. La caractéristique de la notation numérique, à savoir des symboles avec des valeurs locales et intrinsèques (arithmétique), implique un état de civilisation au moment de son invention. La connaissance actuelle des niveaux mathématiques de ces peuples anciens, auxquelles cette section est consacrée, est imparfaite et les notes suivantes doivent être considérées comme un résumé de s conclusions les plus probables, et l'histoire des mathématiques commence avec les sections symboliques.
De nombreux domaines des mathématiques sont apparus avec l'étude de problèmes réels, avant que les règles et concepts sous-jacents soient identifiées et définies comme structures abstraites (en). Par exemple, la géométrie trouve ses origines dans le calcul de longueurs et d'aires dans le monde réel ; l'algèbre est apparue avec le besoin de résoudre des problèmes en arithmétique.
Il n'y a aucun doute sur le fait que la plupart des peuples qui ont laissé derrière eux des documents maitrisaient la numération et la mécanique, et que quelques-uns maitrisaient également des éléments de l'arpentage. En particulier, les Égyptiens se sont intéressés à la géométrie et aux nombres, et les Phéniciens à l'arithmétique pratique, à la comptabilité, la navigation et l'arpentage.
Les résultats atteints par ses peuples semblent avoir été accessibles, sous certaines conditions, aux voyageurs. Il est probable que le savoir des Égyptiens et des Phéniciens sont le résultat d'observations et de mesure, et représente l'expérience accumulée de plusieurs âges.
Débuts de la notation

L'écriture des mathématiques a commencé avec des nombres désignés par des marques de dénombrement, chaque encoche représentant une seule unité. Les symboles numériques consistaient probablement en traits ou encoches taillés dans le bois ou la pierre, et compréhensibles de la même manière pour toutes les nations[note 2]. Par exemple, une encoche dans un os représentait un animal, ou une personne, ou n'importe quoi d'autre. Les peuples avec lesquels les Grecs d'Asie Mineure (parmi lesquels commence la notation dans l'histoire occidentale) étaient susceptibles d'être entrés en contact fréquent étaient ceux qui habitaient le littoral oriental de la Méditerranée, et la tradition grecque assignait uniformément le développement spécial de la géométrie aux Égyptiens, et celle de la science des nombres[note 3] soit aux Égyptiens, soit aux Phéniciens.
Les Égyptiens antiques ont une notation symbolique reposant sur la numération par hiéroglyphes[8] - [9]. Les mathématiques égyptiennes ont un symbole pour 1, 10, 100, 1000, 10 000, 100 000 et 1 000 000. Des chiffres plus petits sont placés à gauche du nombre, car ils sont en chiffres indo-arabes. Plus tard, les Égyptiens utilisent l'écriture hiératique au lieu de hiéroglyphique pour désigner les nombres. Le hiératique est proche de la cursive et remplace plusieurs groupes de symboles par des symboles individuels. Par exemple, les quatre lignes verticales utilisées pour représenter 4 sont remplacés par une seule ligne horizontale. On peut le voir dans le papyrus Rhind (vers 2000-1800 av. J.-C.) et le papyrus de Moscou (vers 1890 av. J.-C.). Le système utilisé par les Égyptiens a été découvert et modifié par de nombreuses autres civilisations méditerranéennes. Les Égyptiens ont aussi des symboles pour les opérations de base : les jambes qui avancent représentent l'addition et les jambes qui reculent sous-entendent la soustraction.
Les Mésopotamiens avaient des symboles pour chaque puissance de 10. Ils écrivent par la suite leurs nombres d'une façon similaire à la numération décimale moderne : au lieu de symboles pour chaque puissance de 10, il ne donne que le coefficient associé à chacune. Chaque chiffre est séparé seulement par un espace, mais du temps d'Alexandre le Grand, ils avaient déjà un symbole désignant le zéro comme emplacement réservé. Les Mésopotamiens utilisaient également un système sexagésimal, de base 60, qui est encore utilisé de nos jours pour les mesures de temps et d'angles. Les mathématiques babyloniennes sont dérivées de plus de 400 tablettes d'argile découvertes dans des fouilles depuis les années 1850[10]. Écrites en cunéiforme, ces tablettes étaient marquées alors que l'argile était encore mou, avant d'être durcies à la cuisson au four ou par le soleil. Certaines sont des devoirs notés. La preuve la plus ancienne de mathématiques écrites date des anciens Sumériens et leur système de métrologie de 3000 av. J.-C.. À partir d'environ 2500 av. J.-C., les Sumériens écrivent leurs tables de multiplication sur des tablettes d'argile et résolvent des exercices de géométrie et des problèmes de division. Les traces les plus anciennes de nombres babyloniens datent de la même période.
La majorité des tablettes d'argile mésopotamiennes date d'entre 1800 et 1600 av. J.-C., et parlent de sujets comme les fractions, l'algèbre, les équations quadratiques et cubiques, et le calcul de nombres réguliers (en), inverses et premiers jumeaux[11]. Les tablettes incluent aussi des tables de multiplication et des méthodes de résolution des équations linéaires et quadratiques. La tablette babylonienne YBC 7289 donne une approximation de √2 exacte à 5 décimales. Les mathématiques babyloniennes utilisant un système sexagésimal (en base 60), dont il reste de nos jours l'usage des 60 seconds en une minute, 60 minutes en une heure, et 360 (60 × 6) degrés dans un cercle, ainsi que les minutes et secondes d'arc pour les fractions de degré. Les avancées babyloniennes en mathématiques ont été facilitées par la grande divisibilité de 60 : l'inverse de tout entier qui est un multiple de diviseurs de 60 a un développement fractionnaire fini en base 60 (dans la base 10, seuls les inverses des multiples de 2 et 5 ont des développements décimaux finis). Aussi, contrairement aux Egyptiens, aux Grecs et aux Romains, les Babyloniens avaient un véritable système à notation positionnelle, où les nombres écrits dans les colonnes de gauche représentaient des valeurs plus grandes, comme dans le système décimal. Il leur manquait cependant un séparateur décimal, aussi la valeur désignée devait souvent être déduite du contexte.
Étape syncopée

Les derniers mots attribués à Archimède sont « Ne perturbe pas mes cercles (en) »(grec moderne : μή μου τοὺς κύκλους τάραττε), une référence aux cercles dans le schéma qu'il étudiait alors qu'un soldat romain le dérangeait.
L'histoire des mathématiques ne peut être reliée avec certitude à une école ou période avant celle des Grecs ioniens, mais l'histoire consécutive peut être divisée en périodes, avec des distinctions assez clairement marquées. Les mathématiques grecques, qui ont débuté avec l'étude de la géométrie, ont tendu dès le début à être déductives et scientifiques. Depuis le IVe siècle, Pythagore est communément reconnu pour avoir découvert le théorème qui porte son nom, un théorème de géométrie qui stipule que dans un triangle rectangle, l'aire du carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés[note 4].
Les textes mathématiques anciens sont disponibles avec la notation des Égyptiens antiques mentionnée précédemment et avec Plimpton 322 (mathématiques babyloniennes vers 1900 av. J.-C.). L'étude des mathématiques en tant que matière à part entière commence au VIe siècle av. J.-C. avec les Pythagoriciens, qui inventèrent le terme "mathématiques" du grec ancien μάθημα (máthêma), signifiant "sujet de l'instruction"[12].
L'influence de Platon a été particulièrement forte en mathématiques et en sciences. Il a contribué à faire la distinction entre les mathématiques pures et les mathématiques appliquées en creusant le fossé entre "l'arithmétique", ce qui désigne la théorie des nombres, et la "logistique", ce qu'on appelle aujourd'hui l'arithmétique. Les mathématiques grecques ont grandement affiné les méthodes (en particulier grâce à l'introduction du raisonnement déductif et de la rigueur mathématique dans la démonstration) et élargi le sujet des mathématiques[13]. Aristote est crédité de ce qui sera plus tard appelée le principe du tiers exclu.
Les mathématiques abstraites[14] sont ce qui traite de la magnitude[note 5] ou quantité, absolument et généralement conférée, sans égard à aucune espèce de grandeur particulière, telle que l'arithmétique et la géométrie. En ce sens, les mathématiques abstraites s'opposent aux mathématiques appliquées, où les propriétés simples et abstraites, et les relations de quantités originellement considérées en mathématiques, sont appliquées aux objets, et par ce moyen se mêlent à des considérations physiques, comme dans l'hydrostatique, l'optique et la navigation[14].
Archimède est généralement considéré comme le plus grand mathématicien de l'Antiquité et l'un des plus grands de tous les temps[15] - [16]. Il a utilisé la méthode d'exhaustion pour calculer l'aire sous l'arc d'une parabole avec la sommation d'une série infinie, et a donné une approximation remarquablement précise de π[17]. Il a également défini la spirale portant son nom, des formules pour les volumes de surfaces de révolution et une système ingénieux pour exprimer de très grands nombres.

Les propriétés 31, 32 et 33 du livre XI, dans le 2e volume du manuscrit, pages 207 et 208.
Dans le développement historique de la géométrie, les étapes de l'abstraction de la géométrie ont été franchies par les Grecs anciens. Les Éléments d'Euclide étant la plus ancienne documentation existante des axiomes de la géométrie plane — bien que Proclus parle d'une axiomatisation antérieure par Hippocrate de Chios[18]. Les Éléments d'Euclide (vers 300 av. J.-C.) sont l'un des plus anciens traités mathématiques grecs existants[note 6] et consiste en treize ouvrages écrits en Alexandrie, réunissant des théorèmes démontrés par d'autres mathématiciens, augmenté de travaux originaux[note 7].
L'œuvre est une collection réussie de définitions, de postulats (axiomes), de propositions (théorèmes et constructions) et de preuves mathématiques des propositions. Le Premier théorème d'Euclide est un lemme qui décrit des propriétés de nombre premiers. Les treize livres influents couvrent la géométrie euclidienne, l'algèbre géométrique et la version grecque ancienne des systèmes algébriques et de la théorie élémentaire des nombres. Il était omniprésent dans le Quadrivium et joue un rôle déterminant dans le développement de la logique, des mathématiques et des sciences.
Diophante d'Alexandrie était l'auteur d'une série de livres appelés Arithmétiques, dont beaucoup sont maintenant perdus. Ces textes traitent de la résolution d'équations algébriques. Boèce a fourni une place aux mathématiques dans le programme d'études au VIe siècle lorsqu'il a inventé le terme « quadrivium » pour décrire l'étude de l'arithmétique, de la géométrie, de l'astronomie et de la musique. Il a écrit De institutione arithmetica, une traduction libre du grec de l'Introduction à l'arithmétique de Nicomaque ; De institutione musica, également dérivé de sources grecques et une série d'extraits des Éléments d'Euclide. Ses travaux étaient plus théoriques que pratiques et constituaient la base de l'étude mathématique jusqu'à la récupération des travaux mathématiques grecs et arabes[19] - [20].
Numération acrophonique et milésienne
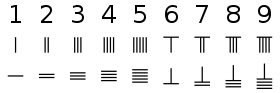
Les Grecs employaient la numération attique[21] qui était basé sur le système des Égyptiens et a ensuite été adapté et utilisé par les Romains. Les chiffres grecs 1 à 4 étaient des lignes verticales, comme dans les hiéroglyphes. Le symbole pour 5 était la lettre grecque Π (pi majuscule), qui est la lettre du mot grec pour cinq, pente. Les nombres 6 à 9 étaient pente avec des lignes verticales à côté. Le nombre 10 était représenté par la lettre (Δ) du mot pour dix, deka, 100 par la lettre du mot pour cent, etc.
La numération ionienne utilise tout son alphabet dont trois lettres archaïques. La notation numérique des Grecs, bien que beaucoup moins pratique que celle actuellement en usage, était formée sur un plan parfaitement régulier et scientifique[22], et pouvait être utilisé avec un effet acceptable comme instrument de calcul, un cas le système romain était totalement inapplicable. Les Grecs divisaient les vingt-quatre lettres de leur alphabet en trois classes, et, en ajoutant un autre symbole à chaque classe, ils avaient des caractères pour représenter les unités, les dizaines et les centaines[23]
| Α (α) | Β (β) | Г (γ) | Δ (δ) | Ε (ε) | Ϝ (ϝ) | Ζ (ζ) | Η (η) | θ (θ) | Ι (ι) | Κ (κ) | Λ (λ) | Μ (μ) | Ν (ν) | Ξ (ξ) | Ο (ο) | Π (π) | Ϟ (ϟ) | Ρ (ρ) | Σ (σ) | Τ (τ) | Υ (υ) | Φ (φ) | Χ (χ) | Ψ (ψ) | Ω (ω) | Ϡ (ϡ) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Ce système est apparu au IIIe siècle av. J.-C., avant que les lettres digamma (Ϝ), koppa (Ϟ) et sampi (Ϡ) ne deviennent obsolètes. Lorsque les lettres minuscules se sont différenciées des lettres majuscules, les premières ont été utilisées comme symboles de notation. Les multiples de 1000 étaient écrits comme les neuf nombres avec un trait devant eux : ainsi mille était ", α", deux mille était ", β", etc. M (pour μὐριοι, comme dans "myriade") était utilisé pour multiplier des nombres par dix mille. Par exemple, le nombre 88 888 888 s'écrirait M,ηωπη*ηωπη[24].
Le raisonnement mathématique grec était presque entièrement géométrique (bien qu'il soit souvent utilisé pour raisonner sur des sujets non directement liés à la géométrie tels que la théorie des nombres), et par conséquent les Grecs n'avaient aucun intérêt pour les symboles algébriques. La grande exception était Diophante d'Alexandrie, le grand algébriste[25]. Son Arithmetica était l'un des textes à utiliser des symboles dans les équations ; si l'écriture n'était pas complètement symbolique, ce l'était beaucoup plus que les livres précédents. Un nombre inconnu était noté s, son carré était noté , son cube était , sa quatrième puissance était , et la cinquième puissance était [26] - [note 8]
Notation chinoise

Les Chinois utilisaient des nombres proches du système unaire[27]. Les nombres 1 à 4 sont représentés par des barres horizontales ; le 5 est symbolisée par un X entre deux traits horizontaux, proche du 10 du système romain. De nos jours, le système huāmǎ n'est utilisé que pour l'affichage des prix dans les marchés chinois ou les reçus manuscrits.
Dans l'histoire chinoise, il y avait ceux qui connaissaient les sciences de l'arithmétique, de la géométrie, de la mécanique, de l'optique, de la navigation et de l'astronomie. Les mathématiques chinoises ont émergé indépendamment au XIe siècle av. J.-C.[28]. Il est presque certain que les Chinois connaissaient plusieurs résultats mathématiques ou plutôt architecturaux[note 9]; avec des machines mécaniques[note 10]; qu'ils connaissaient la propriété caractéristique de l'aiguille aimantée ; et savaient que les événements astronomiques se produisaient par cycles. Les Chinois de cette époque avaient tenté de classer ou d'étendre les règles d'arithmétique ou de géométrie qu'ils connaissaient, et d'expliquer les causes des phénomènes qu'ils connaissaient auparavant. Les Chinois ont indépendamment développé des nombres très grands et les nombres négatifs, décimauxs, un système décimal à notation positionnelle, un système binaire, l'algèbre, la géométrie et la trigonométrie.
Les mathématiques chinoises ont apporté leurs premières contributions, y compris un système de notation positionnelle[29] - [30]. Le théorème géométrique connu des anciens Chinois connaissaient était applicable dans certains cas (à savoir le rapport des côtés)[note 11]. C'est que des théorèmes géométriques qui peuvent être démontrés dans la voie quasi-expérimentale de superposition leur étaient également connus. En arithmétique, leurs connaissances semblent s'être limitées à l'art du calcul au moyen du boulier et au pouvoir d'exprimer les résultats par écrit.
La connaissance actuelle des premiers résultats des Chinois, si faible soit-elle, est plus complète que celle de la plupart de leurs contemporains. Il est donc instructif et sert à illustrer le fait que l'on peut savoir qu'une nation peut posséder des compétences considérables dans les arts appliqués, mais que la connaissance des mathématiques ultérieures sur lesquelles ces arts sont fondés peut être limitée. La connaissance des mathématiques chinoises avant 254 av. J.-C. est quelque peu fragmentaire, et même après cette date, les traditions manuscrites sont obscures. Les dates des siècles avant la période classique sont généralement considérées comme conjecturales par les érudits chinois à moins qu'elles ne soient accompagnées de preuves archéologiques vérifiées.
Comme dans d'autres sociétés anciennes, l'accent était mis sur l'astronomie afin de perfectionner le calendrier agricole et d'autres tâches pratiques, et non sur l'établissement de systèmes formels. Les fonctions du Conseil chinois des mathématiques se limitaient à la préparation annuelle d'un almanach, des dates et des prédictions dans lesquelles il était réglementé. Les anciens mathématiciens chinois n'ont pas développé d'approche axiomatique, mais ont fait des progrès dans le développement d'algorithmes et l'algèbre. La construction de l'algèbre chinoise a atteint son apogée au XIIIe siècle, lorsque Zhu Shijie a inventé la méthode des quatre inconnues.
Du fait d'évidentes barrières linguistiques et géographiques, ainsi que de contenu, les mathématiques chinoises et celles du monde méditerranéen antique sont supposées s'être développées de manière plus ou moins indépendante jusqu'à l'époque où Les Neuf Chapitres sur l'art mathématique a atteint sa forme définitive, tandis que le Livre sur les nombres et le calcul et le Huainanzi sont à peu près contemporains des mathématiques grecques classiques. Un échange d'idées à travers l'Asie à travers des échanges culturels connus depuis au moins l'époque romaine est probable. Souvent, des éléments de mathématiques des premières sociétés correspondent à des résultats rudimentaires trouvés plus tard dans des branches des mathématiques modernes telles que la géométrie ou la théorie des nombres. Le théorème de Pythagore par exemple, il a été attesté à l'époque du duc de Zhou. Il a également été démontré que la connaissance du triangle de Pascal existait en Chine des siècles avant Pascal[31], comme par Shen Kuo.

L'état de la trigonométrie en Chine a lentement commencé à changer et à progresser pendant la dynastie Song (960-1279), où les mathématiciens chinois ont commencé à mettre davantage l'accent sur le besoin de trigonométrie sphérique dans la science calendaire et les calculs astronomiques[32]. Le polymathe scientifique, mathématicien et fonctionnaire chinois Shen Kuo (1031-1095) a utilisé des fonctions trigonométriques pour résoudre des problèmes mathématiques de cordes et d'arcs[32]. Sal Restivo écrit que les travaux de Shen sur les longueurs d'arcs de cercles ont servi de base à la trigonométrie sphérique développée au XIIIe siècle par le mathématicien et astronome Guo Shoujing (1231-1316). Comme l'affirment les historiens L. Gauchet et Joseph Needham, Guo Shoujing a utilisé la trigonométrie sphérique dans ses calculs pour améliorer le système de calendrier chinois et l'astronomie chinoise[32].
La science mathématique des Chinois intégrera le travail et l'enseignement des missionnaires arabes ayant des connaissances de la trigonométrie sphérique qui sont venus en Chine au cours du XIIIe siècle.
Notations et nombres indo-arabes
Bien que l'origine de notre système actuel de notation numérique soit ancienne, il ne fait aucun doute qu'il était utilisé par les Hindous il y a plus de deux mille ans. La notation algébrique du mathématicien indien, Brahmagupta, était syncopée. L'addition était indiquée en plaçant les nombres côte à côte, la soustraction en plaçant un point sur le terme à soustraire et la division en plaçant le diviseur sous le dividende, de façon similaire à la notation actuelle mais sans la barre. La multiplication, l'évolution et les quantités inconnues étaient représentées par des abréviations de termes appropriés[33]. Le Système de numération indo-arabe et les règles d'utilisation de ses opérations, en usage dans le monde aujourd'hui, ont probablement évolué au cours du premier millénaire av. J.-C. en Inde et a été transmis à l'ouest via les mathématiques islamiques[34] - [35].

Malgré leur nom, les chiffres arabes trouvent leurs racines en Inde. La raison de ce nom impropre est que les Européens ont vu les chiffres utilisés dans un livre arabe, Traité du système de numération des Indiens, par Muḥammad ibn Mūsā al-Khwārizmī. Ce dernier a écrit plusieurs livres importants sur les chiffres indo-arabes et sur les méthodes de résolution des équations. Son livre Traité du système de numération des Indiens, écrit vers 825, ainsi que l'œuvre de Al-Kindi[note 12], ont joué un rôle déterminant dans la diffusion des mathématiques indiennes et des chiffres indiens en Occident. Al-Khwarizmi n'a pas revendiqué les chiffres comme arabes, mais sur plusieurs traductions latines, le fait que les chiffres étaient d'origine indienne a été perdu. Le mot algorithme est dérivé de la latinisation du nom d'Al-Khwārizmī, Algoritmi, et le mot algèbre du titre d'un de ses ouvrages, Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala (Abrégé du calcul par la restauration et la comparaison).
Les mathématiques arabes ont développé et développé les mathématiques connues des civilisations d'Asie centrale[36]. Al-Khwārizmī a donné une explication exhaustive de la solution algébrique des équations quadratiques à racines positives[37], et Al-Khwārizmī devait enseigner l'algèbre sous une forme élémentaire et pour elle-même[38]. Al-Khwārizmī a également discuté de la méthode fondamentale de "réduction" et d'"équilibrage", se référant à la transposition de termes soustraits de l'autre côté d'une équation, c'est-à-dire l'annulation de termes similaires des deux côtés de l'équation. C'est l'opération qu'al-Khwārizmī décrivait à l'origine comme al-jabr[39]. Son algèbre ne se préoccupe plus non plus « d'une série de problème mathématiques à résoudre, mais d'une exposition qui part de termes primitifs dont les combinaisons doivent donner tous les prototypes possibles pour équations, qui constituent désormais explicitement le véritable objet d'étude." Al-Khwārizmī a également étudié une équation pour elle-même et "de manière générique, dans la mesure où elle n'émerge pas simplement au cours de la résolution d'un problème, mais est spécifiquement appelée à définir une classe infinie de problèmes[40]".
Al-Karaji, dans son traité al-Fakhri, étend la méthode pour incorporer des puissances entières et des racines entières de quantités inconnues[note 13] - [41]. L'historien des mathématiquesFranz Woepcke[42], a félicité Al-Karaji d'être "le premier à avoir introduit la théorie du calcul algébrique". Toujours au Xe siècle, Abu l-Wafa traduisit les œuvres de Diophante en arabe. Ibn al-Haytham développera la géométrie analytique. Al-Haytham a dérivé la formule de la somme des quatrièmes puissances, en utilisant une méthode facilement généralisable pour déterminer la formule générale de la somme de toutes les puissances intégrales. Al-Haytham a effectué une intégration afin de trouver le volume d'un paraboloïde, et a pu généraliser son résultat pour les intégrales de polynômes jusqu'au quatrième degré][note 14] - [43]. À la fin du XIe siècle, Omar Khayyam développera la géométrie algébrique, écrira Discussions of the Difficulties in Euclid[note 15], et a écrit sur la solution géométrique générale des équations cubiques. Nasir al-Din al-Tusi (Nasireddin) a fait des progrès dans la trigonométrie sphérique. Les mathématiciens musulmans de cette période incluent l'ajout du point décimal aux chiffres arabes.
Les symboles des chiffres arabes modernes utilisés dans le monde sont apparus pour la première fois en Afrique du Nord islamique au Xe siècle. Une variante distincte de l'arabe occidental des chiffres arabes orientaux a commencé à émerger vers le Xe siècle dans le Maghreb et Al-Andalus (parfois appelés chiffres ghubar, bien que le terme ne soit pas toujours accepté), qui est l'ancêtre direct des chiffres arabes modernes utilisés dans le monde entier[44].
De nombreux textes grecs et arabes sur les mathématiques ont alors été traduits en latin, ce qui a conduit à un développement ultérieur des mathématiques dans l'Europe médiévale. Au XIIe siècle, des érudits se sont rendus en Espagne et en Sicile à la recherche de textes scientifiques arabes, y compris d'al-Khwārizmī[note 16] et le texte complet des Éléments d'Euclide[45] - [46]. L'un des livres européens qui préconisaient l'utilisation des chiffres était Liber abaci, de Léonard de Pise, mieux connu sous le nom de Fibonacci. Liber Abaci est mieux connu pour le problème mathématique que Fibonacci y a écrit à propos d'une population de lapins. La croissance de la population a fini par être une suite de Fibonacci, où un terme est la somme des deux termes précédents.
Étape symbolique
- Symbole par date d'apparition

Débuts de l'arithmétique et de la multiplication
La transition vers l'algèbre symbolique, où seuls les symboles sont utilisés, peut d'abord être vue dans les travaux de Ibn al-Banna' al-Marrakushi (1256-1321) et Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412-1482)[47] - [48]. Al-Qalasādī était le dernier grand algébriste arabe, qui a amélioré la notation algébrique précédemment utilisée dans le Maghreb par Ibn al-Banna[49]. Contrairement aux notations syncopées de leurs prédécesseurs, Diophante et Brahmagupta, qui manquaient de symboles pour les opérations mathématiques[50]. La notation algébrique d'al-Qalasadi a été la première d'avoir des symboles pour ces fonctions et était donc "les premiers pas vers l'introduction du symbolisme algébrique". Il a représenté symboles mathématiques en utilisant des caractères de l'alphabet arabe[49].

Le XIVe siècle a vu le développement de nouveaux concepts mathématiques pour étudier un large éventail de problèmes[51]. Les deux symboles arithmétiques largement utilisés sont l'addition et la soustraction, + et -. Le signe plus était utilisé vers 1360 par Nicole Oresme[52] - [note 17] dans son ouvrage Algorismus proportionum[53]. On pense qu'il s'agit d'une abréviation du "et" latin, de la même manière que le signe esperluette a également commencé par "et". Oresme de l'Université de Paris et l'italien Giovanni di Casali ont indépendamment fourni des démonstrations graphiques de la distance parcourue par un corps subissant un mouvement uniformément accéléré, affirmant que l'aire sous la ligne représentant l'accélération constante et représentait la distance totale parcourue. Le signe moins a été utilisé en 1489 par Johannes Widmann dans Mercantile Arithmetic ou Behende und hüpsche Rechenung auff allen Kauffmanschafft[54]. Widmann a utilisé le symbole moins avec le symbole plus, pour indiquer respectivement le déficit et l'excédent. Dans Summa de arithmetica, geometria, de proportioni et de proportionalita[note 18], Luca Pacioli utilisait des symboles pour les symboles plus et moins et contenait algèbre[note 19].
Au XVe siècle, Ghiyath al-Kashi a calculé la valeur de π à la 16e décimale près. Kashi disposait également d'un algorithme pour calculer les nièmes racines[note 20]. En 1533, la table des sinus et cosinus de Regiomontanus fut publiée. Scipione del Ferro et Niccolò Fontana Tartaglia ont découvert des solutions pour les équations cubiques. Gerolamo Cardano les a publiés dans son livre de 1545 Ars Magna, ainsi qu'une solution pour les équations quartiques, découverte par son élève Ludovico Ferrari. Le symbole radical, soit pour la racine carrée, a été introduit par Christoff Rudolff, le symbole évoquant un r minuscule, pour radix. L'important travail de Michael Stifel Arithmetica integra contenait d'importantes innovations dans la notation mathématique. En 1556, Tartaglia a utilisé des parenthèses pour le groupement de priorité. En 1557, Robert Recorde publie The Whetstone of Witte (en) qui introduit le signe égal (=), ainsi que les signes plus et moins pour le lecteur anglais. En 1564, Gerolamo Cardano analyse les jeux de hasard, posant les bases de la théorie des probabilités. En 1572, Raphaël Bombelli publie L'Algebra dans laquelle il montre comment traiter les quantités imaginaires qui pourraient apparaître dans la formule de Cardano pour résoudre les équations cubiques. Le livre de Simon Stevin De Thiende ("l'art des dixièmes"), publié en néerlandais en 1585, contient un traitement systématique de la notation décimale, qui a influencé tous les travaux ultérieurs sur le système de nombres réels. L'Algèbre nouvelle (1591) de François Viète introduit la manipulation notationnelle moderne des expressions algébriques. Pour la navigation et les cartes précises de vastes zones, la trigonométrie est devenue une branche majeure des mathématiques. Bartholomäus Pitiscus a inventé le mot "trigonométrie", publiant Trigonometria en 1595.
John Napier est surtout connu comme l'inventeur des logarithmes[note 21] - [55] et a rendu courant l'utilisation du point décimal en arithmétique et en mathématiques[56] - [57]. Après Napier, Edmund Gunter a créé l'échelle logarithmique sur lesquelles les règles à calcul sont basées, c'est William Oughtred qui utilisait deux de ces règles glissant l'une par l'autre pour effectuer une multiplication et une division directement ; et il est crédité comme l'inventeur de la règle à calcul en 1622. En 1631, Oughtred a introduit le signe de multiplication (×) son signe de proportionnalité, ∷, et les abréviations sin et cos pour les fonctions sinus et cosinus[58]. Albert Girard a également utilisé les abréviations sin, cos et tan pour les fonctions trigonométriques dans son traité.
Johannes Kepler a été l'un des pionniers des applications mathématiques des infinitésimaux[note 22]. René Descartes est crédité comme le père de la géométrie analytique, le pont entre l'algèbre et la géométrie[note 23], crucial pour la découverte du calcul infinitésimal et de l'analyse mathématique. Au XVIIe siècle, Descartes a introduit les coordonnées cartésiennes qui ont permis le développement de la géométrie analytique. Bernhard Riemann et Gauss ont généralisé les concepts de géométrie pour développer les géométries non euclidiennes. Blaise Pascal a influencé les mathématiques tout au long de sa vie. Son Traité sur le triangle arithmétique de 1653 décrit une présentation tabulaire pratique des coefficient binomiaux, ce qu'on appelle aujourd'hui le triangle de Pascal. Pierre de Fermat et Blaise Pascal étudieront la probabilité[note 24]. John Wallis a introduit le symbole de l'infini . Il a également utilisé cette notation pour les infinitésimaux[note 25]. En 1657, Christian Huygens publie le traité de probabilité, De ratiociniis in ludo aleae[59].
Johann Rahn a introduit le signe de division (÷, une variante de l'obélus réutilisée) et le signe donc en 1659. William Jones a utilisé π dans Synopsis palmariorum mathesios[60] en 1706 parce que c'est la lettre initiale du mot grec περιμετρον (perímétron), qui signifie périmètre en grec. Cet usage a été popularisé en 1737 par Euler. En 1734, Pierre Bouguer utilise une double barre horizontale sous le signe d'inégalité[61].
Notation de la dérivation : Leibniz et Newton
| Notation différentielle | |
|---|---|
| |
L'étude de l'algèbre linéaire a émergé de l'étude des déterminants, qui ont été utilisés pour résoudre des systèmes linéaires. Le calcul comportait deux principaux systèmes de notation, chacun créé par l'un des créateurs : celui développé par Isaac Newton et la notation développée par Gottfried Leibniz. La notation de Leibniz est la notation la plus utilisée aujourd'hui. Celui de Newton était simplement un point ou un tiret placé au-dessus de la fonction[note 26]. Dans l'usage moderne, cette notation désigne généralement les dérivées de quantités physiques par rapport au temps, et est fréquemment utilisé dans la science de la mécanique. Leibniz, d'autre part, a utilisé la lettre d comme préfixe pour indiquer la différenciation, et a introduit la notation représentant les dérivés comme s'il s'agissait d'un type spécial de fraction[note 27]. Cette notation rend explicite la variable par rapport auquel la dérivée de la fonction est prise. Leibniz a également créé la notation de l'intégrale . Le symbole est un S allongé, représentant le mot latin Summa, signifiant "somme". Lors de la recherche d'aires sous des courbes, l'intégration est souvent illustrée en divisant l'aire en une infinité de rectangles hauts et fins, dont les aires sont ajoutées. Ainsi, le symbole intégral est un s allongé, pour somme.
Fonctions
Les lettres de l'alphabet de nos jours sont utilisées comme symboles de quantité ; et bien qu'il existe une grande diversité quant au choix des lettres, il existe plusieurs conventions établies par la suite[22]. Ici donc dans l'histoire des équations, les premières lettres de l'alphabet étaient à titre indicatif appelées coefficients, les dernières lettres les inconnues (un incerti ordinis). En géométrie algébrique, encore une fois, une règle similaire doit être observée, les dernières lettres de l'alphabet y désignant les coordonnées variables ou courantes. Certaines lettres, telles que π ou e, ont été par consentement universel appropriées comme symboles des nombres fréquents (en l'occurrence 3,14159..., et 2,7182818....[note 28]), et leur utilisation dans toute autre acception doit être évitée autant que possible[22] Les lettres aussi devaient être employées comme symboles d'opération, et avec elles autres caractères d'opération arbitraires mentionnés précédemment. Les lettres et doivent être appropriées comme symboles opératoires dans le calcul différentiel et le calcul intégral, et dans le calcul des différences[22]. Dans la notation fonctionnelle, une lettre, en tant que symbole d'opération, est combinée avec une autre qui est considérée comme un symbole de quantité[22] - [note 29].
À partir de 1718, Thomas Twinin a utilisé la barre oblique, en la dérivant de la barre de fraction horizontale arabe. Pierre-Simon de Laplace a développé l'opérateur différentiel laplacien[note 30]. En 1750, Gabriel Cramer développe la règle de Cramer pour résoudre les systèmes linéaires.
Euler et notation prime
Leonhard Euler était l'un des mathématiciens les plus prolifiques de l'histoire, et aussi un inventeur prolifique de la notation canonique. Ses contributions incluent son utilisation de e pour représenter la base du logarithme naturel. On ne sait pas exactement pourquoi e a été choisi, mais c'est probablement parce que les quatre lettres de l'alphabet étaient déjà couramment utilisées pour représenter des variables et d'autres constantes. Euler a utilisé π pour représenter pi de manière cohérente. L'utilisation de π a été suggérée par William Jones, qui l'a utilisé comme raccourci pour périmètre. Euler a utilisé i pour représenter l'unité imaginaire, qu'on note abusivement √-1, bien qu'il ait plus tôt été utilisé comme un nombre infini[note 31] - [note 32]. Pour la sommation, Euler a utilisé le sigma majuscule, [note 33]. Pour les fonctions, Euler a utilisé la notation pour représenter une fonction de . En 1730, Euler décrit la fonction gamma[note 34]. En 1736, Euler produit son article sur les problème des sept ponts de Königsberg[62] initiant l'étude de la théorie des graphes.
Le mathématicien William Emerson développe le signe de proportionnalité ∝[63] - [64] - [65]. Bien plus tard dans les expressions abstraites de la valeur de divers phénomènes proportionnels, la notation en "parties par" (en) deviendrait utile comme un ensemble de pseudo-unités pour décrire de petites valeurs de diverses quantités sans dimension. Le marquis de Condorcet, en 1768, avança le signe de la dérivée partielle[note 35]. En 1771, Alexandre-Théophile Vandermonde déduit l'importance des traits topologiques lorsqu'il discute de la propriétés des nœuds liée à la géométrie de position. Entre 1772 et 1788, Joseph-Louis Lagrange reformule les formules et les calculs de la mécanique "newtonienne" classique, appelée mécanique lagrangienne. Le symbole prime pour les dérivées a également été créé par Lagrange.
« Mais à notre opinion les vérités de ce genre doivent être tirées des notions plutôt que des notations. »
— Carl Friedrich Gauss[note 36]
Gauss, Hamilton et notations matricielles
Au début du XIXe siècle, Carl Friedrich Gauss développe le signe d'identité pour la relation de congruence ≡ et, pour la réciprocité quadratique, le symbole partie entière. Gauss contribue aux fonctions d'une variable complexe, en géométrie, et la convergence des séries. Il donne des preuves satisfaisantes du théorème fondamental de l'algèbre et la loi de réciprocité quadratique. Gauss a développé la théorie de la résolution de systèmes linéaires en utilisant l'élimination gaussienne, initialement répertoriée comme une avancée en géodésie[66]. Il développera également le signe produit. Toujours à cette époque, Niels Henrik Abel et Évariste Galois[note 37] leurs travaux sur la racines des équations, reliant la théorie des groupes et celle des corps commutatifs.
Après les années 1800, Christian Kramp promouvra la notation factorielle lors de ses recherches sur la fonction factorielle généralisée qui s'appliquait aux non-entiers[67]. Joseph Diez Gergonne a introduit les signes d'inclusion[note 38]. Johann Peter Gustav Lejeune Dirichlet a développé les séries L de Dirichlet pour donner la pFreuve du théorème de Dirichlet sur les suites arithmétiques et a commencé la théorie analytique des nombres[note 39]. En 1828, Gauss a prouvé son Theorema egregium (théorème remarquable en latin), établissant la propriété des surfaces. Dans les années 1830, George Green a développé la fonction de Green. En 1829. Charles Gustave Jacob Jacobi publie Fundamenta nova theoriae functionum ellipticarum (en) avec ses fonctions thêta elliptiques. En 1841, Karl Weierstrass, le "père de l'analyse" moderne, a élaboré le concept de valeur absolue et de déterminant d'une matrice.
La notation matricielle (en) sera plus amplement développée par Arthur Cayley dans ses trois articles, sur des sujets qui avaient été suggérés par la lecture de la mécanique analytique de Lagrange[68] et quelques ouvrages de Laplace. Cayley a défini le produit matriciel et l'inverse d'une matrice. Cayley a utilisé une seule lettre pour désigner une matrice[69], traitant ainsi une matrice comme un objet agrégé. Il a également réalisé le lien entre les matrices et les déterminants[70], et écrit « There would be many things to say about this theory of matrices which should, it seems to me, precede the theory of determinants » (« Il y aurait beaucoup de choses à dire sur cette théorie des matrices qui devrait, il me semble, précéder la théorie des déterminants. »)[71].
« [... The mathematical quaternion] has, or at least involves a reference to, four dimensions. »
— William Rowan Hamilton[note 40]
William Rowan Hamilton introduit le symbole nabla (ou, plus tard appelé del) pour une différentielle vectorielle[72] - [73]. Celui-ci était auparavant utilisé par Hamilton comme un symbole d'opérateur[74]. Hamilton a réécrit la mécanique newtonienne, maintenant appelée mécanique hamiltonienne. Ce travail s'est avéré central pour l'étude moderne des théories classiques des champs telles que l'électromagnétisme. Cela était également important pour le développement de la mécanique quantique[note 41]. En mathématiques, il est peut-être mieux connu comme l'inventeur de la notation des quaternions[note 42] et des biquaternions. Hamilton a également introduit le mot "tenseur" en 1846[75] - [note 43]. James Cockle développe la tessarine[note 44] et, en 1849, les coquaternions. En 1848, James Joseph Sylvester introduit dans l'algèbre matricielle le terme matrice[note 45].
Maxwell, Clifford et notations de Ricci
La réalisation la plus importante de Maxwell a été de formuler un ensemble d'équations qui réunissait des observations, des expériences et des équations auparavant sans rapport avec l'électricité, le magnétisme et l'optique en une théorie cohérente[76].
En 1864, James Clerk Maxwell a réduit toutes les connaissances alors actuelles sur l'électromagnétisme en un ensemble lié d'équations différentielles avec 20 équations de 20 variables, contenues dans A Dynamical Theory of the Electromagnetic Field (en)[77]. La méthode de calcul qu'il est nécessaire d'employer a été donnée par Lagrange, et ensuite développée, avec quelques modifications, par les équations de Hamilton. Il est généralement appelé principe de Hamilton ; lorsque les équations sous leur forme originale sont utilisées, elles sont appelées équations de Lagrange. En 1871, Richard Dedekind a appelé un ensemble de nombres réels ou complexes fermé par les quatre opérations arithmétiques un champ. En 1873, Maxwell présente A Treatise on Electricity and Magnetism (en).
En 1878, William Kingdon Clifford a publié Elements of Dynamic (en)[78]. Clifford a développé les split-biquaternions[note 46], qu'il a appelé moteurs algébriques. Clifford a évité l'étude des quaternions en séparant le produit scalaire et le produit vectoriel de deux vecteurs de la notation complète des quaternions[note 47]. Cette approche a rendu le calcul vectoriel disponible pour les ingénieurs et autres personnes travaillant en trois dimensions et sceptique de l'effet lead–lag[note 48] dans la quatrième dimension[note 49]. Les notations vectorielles (en) courantes sont utilisées lorsque l'on travaille avec des vecteurs qui sont spatiaux ou plus abstraits membres de espace vectoriels, tandis que la notation d'angle (en) (ou notation phaseur) est une notation utilisée en électronique.
En 1881, Leopold Kronecker a défini ce qu'il a appelé un "domaine de rationalité", qui est une extension de corps de l'ensemble des nombres rationnels en termes modernes[79]. En 1882, Husseïn Tevfik Pacha a écrit le livre intitulé Linear Algebra[80]. La théorie atomique de l'éther de Lord Kelvin (années 1860) a conduit Peter Guthrie Tait, en 1885, à publier une table topologique de nœuds avec jusqu'à dix croisements connue sous le nom de conjectures de Tait. En 1893, Heinrich M. Weber donna la définition claire d'un corps abstrait[note 50]. Le calcul tensoriel a été développé par Gregorio Ricci-Curbastro entre 1887 et 1896, présenté en 1892 sous le titre calcul différentiel absolu[81], et l'usage contemporain de "tenseur" a été énoncé par Woldemar Voigt en 1898[82]. En 1895, Henri Poincaré publie Analysis Situs[83]. En 1897, Charles Proteus Steinmetz publiera Théorie et calcul des phénomènes de courant alternatif[84], avec l'aide d'Ernst J. Berg[85].
Des formules mathématiques aux tenseurs
« The above proposition is occasionally useful. »
En 1895 Giuseppe Peano publie son Formulario Mathematico[86], un effort pour résumer les mathématiques dans un texte concis basé sur des symboles spéciaux. Il fournit la définition d'un espace vectoriel et d'une application linéaire. Il introduit également le signe d'intersection, le signe d'union, le signe d'inclusion (est un élément de) et le quantificateur existentiel (il existe)[note 51]. Peano transmettra à Bertrand Russell son travail en 1900 lors d'une conférence à Paris ; cela a tellement impressionné Russell que celui-ci aussi a été pris par la volonté de rendre les mathématiques de manière plus concise. Le résultat fut Principia Mathematica écrit avec Alfred North Whitehead. Ce traité marque un tournant dans la littérature moderne où le symbole est devenu dominant. Le cinquième est apparu en 1908 et comprenait 4 200 formules et théorèmes.
Gregorio Ricci-Curbastro et Tullio Levi-Civita ont popularisé la notation tensorielle vers 1900[87].
Logique mathématique et abstraction
| Abstraction | |
|---|---|
| |
Au début de cette période, le programme d'Erlangen de Felix Klein a identifié le thème sous-jacent de diverses géométries, définissant chacune d'elles comme l'étude des propriétés invariantes sous un groupe donné de symétries. Ce niveau d'abstraction a révélé des liens entre la géométrie et l'algèbre abstraite. Georg Cantor, inventeur de la théorie des ensembles, introduira le nombre aleph pour les cardinaux d'ensembles transfinis[note 52]. Sa notation pour les nombres cardinaux était la lettre hébraïque (aleph) avec un entier naturel en indice ; pour les ordinaux, il emploie la lettre grecque ω (oméga). Cette notation est encore utilisée aujourd'hui dans la notation ordinale (en) d'une séquence finie de symboles d'un alphabet fini qui nomme un nombre ordinal selon un schéma qui donne un sens à la langue. Sa théorie a provoqué une grande controverse (en). Cantor, dans son étude des séries de Fourier, considère des ensembles de points dans l'espace euclidien.
Après le tournant du XXe siècle, Josiah Willard Gibbs introduit en chimie physique le point médian pour le produit scalaire et la croix de multiplication pour le produit vectoriel. Il fournira également une notation pour les produits scalaires et vectoriels, qui a été introduite dans Analyse vectorielle. En 1904, Ernst Zermelo promeut l'axiome du choix et sa preuve du théorème du bon ordre[88]. Bertrand Russell introduira peu après la disjonction logique (OU) en 1906. La même année, Henri Poincaré publiera Sur la dynamique de l’électron[89] et René Maurice Fréchet introduit l'espace métrique[90]. Plus tard, Gerhard Kowalewski et Cuthbert Edmund Cullis (en)[91] - [92] - [93] vont introduire avec succès les notations matricielles, respectivement avec parenthèses et avec crochets. Après 1907, des mathématiciens tels que Max Dehn, J. W. Alexander, étudient les nœuds du point de vue du groupe de nœuds et les invariants par la théorie de l'homologie, comme le polynôme d'Alexander. En 1908, les théorèmes de structure de Joseph Wedderburn ont été formulés pour les algèbres sur un corps de dimension finie. Toujours en 1908, Ernst Zermelo proposa la propriété "définie" et la première théorie axiomatique des ensembles, la théorie des ensembles de Zermelo. En 1910, Ernst Steinitz a publié l'article influent Algebraische Theorie der Körper (Théorie algébrique des corps)[note 53]. En 1911, Steinmetz publiera Theory and Calculation of Transient Electric Phenomena and Oscillations.
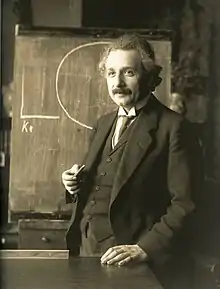
Albert Einstein, en 1916, introduit la notation d'Einstein[note 54] qui réduit l'écriture d'une somme sur un ensemble de termes indicés dans une formule. Arnold Sommerfeld crée le signe de l'intégrale de contour en 1917. La même année, Dmitry Mirimanoff propose l'axiome de régularité. In 1919, Theodor Kaluza résout les équations de la relativité générale en utilisant cinq dimensions (en), les résultats faisant émerger les équations électromagnétiques[94].
Cela sera publié en 1921 dans Zum Unitätsproblem der Physik[95] - [96]. En 1922, Abraham Fraenkel et Thoralf Skolem ont proposé indépendamment de remplacer le Schéma d'axiomes de compréhension par le schéma d'axiomes de remplacement. Toujours en 1922, la théorie des ensembles de Zermelo-Fraenkel a été développée. En 1923, Steinmetz publiera Four Lectures on Relativity and Space[97]. Vers 1924, Jan Arnoldus Schouten développera la notation et le formalisme moderne pour le cadre du tenseur de Ricci lors des applications du calcul différentiel absolu à la relativité générale et à la géométrie différentielle au début du XXe siècle[note 55] - [98] - [99] - [100]. En 1925, Enrico Fermi décrit un système régissant plusieurs particules identiques qui obéissent au principe d'exclusion de Pauli, développant par la suite l'équation de diffusion. En 1926, Oskar Klein développe la théorie de Kaluza–Klein. En 1928, Emil Artin résume la théorie des anneaux avec les anneaux artiniens. En 1933, Andreï Kolmogorov introduit les Axiomes de Kolmogorov. En 1937, Bruno de Finetti déduit sa conception « opérationnelle subjective (en) ».
Symbolisme mathématique
L'abstraction mathématique a commencé comme un processus d'extraction de l'essence sous-jacente d'un concept mathématique[101] - [102], supprimant toute dépendance vis-à-vis des objets du monde réel avec lesquels il aurait pu être connecté à l'origine[103], et en le généralisant afin qu'il ait des applications plus larges ou qu'il corresponde à d'autres descriptions abstraites de phénomènes équivalents. Deux domaines abstraits des mathématiques modernes sont la théorie des catégories et la théorie des modèles. Bertrand Russell, disait : « Le langage ordinaire est totalement inadapté pour exprimer ce que la physique affirme réellement, puisque les mots de la vie quotidienne ne sont pas suffisamment abstraits. Seules les mathématiques et la logique mathématique peut en dire aussi peu que le physicien veut dire. »[104] Cependant, on peut substituer les mathématiques aux objets du monde réel, et errer à travers équation après équation, et peut construire une structure de concept qui n'a aucun rapport avec la réalité[105].
La logique symbolique étudie les propriétés purement formelles des chaînes de symboles. L'intérêt pour ce domaine provient de deux sources. Premièrement, la notation utilisée dans la logique symbolique peut être considérée comme représentant les mots utilisés dans la logique philosophique. Deuxièmement, les règles de manipulation des symboles trouvées dans la logique symbolique peuvent être implémentées sur un machine informatique. La logique symbolique est généralement divisée en deux sous-domaines, la logique propositionnelle et la logique des prédicats. D'autres logiques intéressantes incluent la logique temporelle, la logique modale et la logique floue. Le domaine de la logique symbolique appelée logique propositionnelle, aussi appelée calcul propositionnel, étudie les propriétés des phrases formées à partir de constantes[note 56] et les opérateurs logiques. Les opérations logiques correspondantes sont respectivement appelées conjonction, disjonction, implication, bicondition (en) et négation. Ces opérateurs sont désignés par mots-clés[note 57] et par notation symbolique.
Certaines des notations logiques mathématiques introduites à cette époque comprennent l'ensemble de symboles utilisés dans l'algèbre booléenne. Cela a été créé par George Boole en 1854. Boole lui-même ne considérait pas la logique comme une branche des mathématiques, mais elle en est venue à être englobée de toute façon. Les symboles trouvés dans l'algèbre booléenne incluent (ET), (OU) et (NON). Avec ces symboles et des lettres pour représenter différentes vérités, on peut faire des déclarations logiques telles que , c'est-à-dire "(a est vrai OU a est pas vrai) est vrai", ce qui signifie qu'il est vrai que a est soit vrai soit faux (c'est-à-dire faux). L'algèbre booléenne a de nombreuses utilisations pratiques telles quelles, mais c'était aussi le début de ce qui serait un grand ensemble de symboles à utiliser en logique[note 58]. La logique des prédicats, appelée à l'origine calcul des prédicats, étend la logique propositionnelle par l'introduction de variables[note 59] et par des sentences contenant des variables, ce qu'on appelle des prédicats, habituellement noté par une lettre majuscule suivi d'une liste de variables, comme P(x) or Q(y, z). Ici un prédicat logique mathématique, un concept fondamental en logique du premier ordre. Les prédicats grammaticaux sont les composants grammaticaux d'une phrase.
De plus, la logique des prédicats permet l'utilisation de quantificateurs représentant TOUT et IL EXISTE. Avec ces symboles logiques et des quantificateurs supplémentaires de la logique des prédicats[note 60], des preuves valides peuvent être faites qui sont irrationnellement artificiel[note 61], mais syntaxiquement correctes[note 62].
Notation de l'incomplétude de Gödel
« À toute classe récursive ω-cohérente κ de formules correspondent des signes de classe r récursifs, tels que ni v Gen r ni Neg (v Gen r) n'appartient à Flg (κ) (où v est la variable libre de r). »
— Kurt Gödel[106]
Alors qu'il démontrait ses théorèmes d'incomplétude[note 63], Kurt Gödel crée une alternative aux symboles normalement utilisés en logiques. Il utilise le codage de Gödel, qui attribue des nombres aux opérations avec des ensembles de nombres, et des variables pour les nombres premiers supérieurs à 10. Avec les nombres de Gödel, les déclarations logiques peuvent être réécrites en une suite de nombres. Gödel pousse ensuite la réflexion, en prenant les n premiers nombres premiers et les mettant à la puissance des nombres de la suite. Ces nombres sont alors multiplés ensemble pour obtenir le produit final, associant ainsi à chaque déclaration son propre nombre[107].
- Exemple
- La déclaration "Il existe un nombre x tel qu'il n'est pas y". Par les symboles de l'algèbre propositionnelle, elle devient :
- .
- Avec les nombres de Gödel, elle devient
- Il y a dix nombres, donc on prend les dix premiers nombres premiers, soit
- Le nombre de Gödel de la proposition s'obtient en faisant le calcul
Notations du début du XXe siècle
L'abstraction de la notation est un processus continu et le développement historique de nombreux sujets mathématiques montre une progression du concret à l'abstrait. Diverses notations d'ensembles (en) seraient développées pour les objets fondamentaux « ensembles ». Vers 1924, David Hilbert et Richard Courant publient Methoden der mathematischen Physik (en)[108]. En 1926, Oskar Klein et Walter Gordon ont proposé l'équation de Klein-Gordon pour décrire les particules relativistes[note 64]. La première formulation d'une théorie quantique décrivant l'interaction rayonnement et matière est due à Paul Adrien Maurice Dirac, qui, en 1920, a été capable pour la première fois de calculer le coefficient d'émission spontanée d'un atome[109].
En 1928, l'équation de Dirac, relativiste, a été formulée par Dirac pour expliquer le comportement de l'électron en mouvement relativiste[note 65]. Dirac a décrit la quantification du champ électromagnétique comme un ensemble d'oscillateurs harmoniques avec l'introduction du concept d'opérateurs de création et d'annihilation (en) de particules. Dans les années suivantes, avec les contributions de Wolfgang Pauli, Eugene Wigner, Pascual Jordan et Werner Heisenberg, et une formulation élégante de l'électrodynamique quantique due à Enrico Fermi[110], les physiciens en sont venus à croire qu'en principe, il serait possible d'effectuer n'importe quel calcul pour n'importe quel processus physique impliquant des photons et des particules chargées.
En 1931, Alexandru Proca développe l'équation de Proca (équation d'Euler-Lagrange)[note 66] pour la théorie vectorielle des mésons des forces nucléaires et la théorie quantique des champs. John Archibald Wheeler en 1937 développe la matrice S. Des études de Félix Bloch avec Arnold Nordsieck (en)[111] et Victor Weisskopf[112], en 1937 et 1939, ont révélé que de tels calculs n'étaient fiables qu'à un premier ordre de théorie des perturbations, un problème déjà signalé par Robert Oppenheimer[113]. Aux ordres supérieurs de la série, des infinis ont émergé, rendant ces calculs dénués de sens et jetant de sérieux doutes sur la cohérence interne de la théorie elle-même. En l'absence de solution à ce problème connue à l'époque, il est apparu qu'une incompatibilité fondamentale existait entre la relativité restreinte et la mécanique quantique.
Dans les années 1930, le Z majuscule à double frappe pour les ensembles de nombres entiers a été créé par Edmund Landau. Nicolas Bourbaki a créé le Q majuscule à double frappe pour les ensembles de nombres rationnels. En 1935, Gerhard Gentzen fabrique des quantificateurs universels. En 1936, le théorème de non définissabilité est énoncé par Alfred Tarski et prouvé[note 67]. En 1938, Gödel propose l'univers constructible dans l'article The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis[114]. André Weil et Nicolas Bourbaki mettront au point le signe ensemble vide en 1939. Cette même année, Nathan Jacobson frappe le C majuscule double pour l'ensemble des nombres complexes.
Dans les années 1930, la notation de Voigt, du nom de Voigt qui l'a développé en 1898, est mise en point pour l'algèbre multilinéaire comme un moyen de représenter un tenseur symétrique en réduisant son ordre. La notation Schoenflies, du nom de Arthur Moritz Schoenflies, est devenue une des deux conventions utilisées pour décrire les groupes ponctuels (l'autre étant la notation de Hermann-Mauguin). À la même période, la notation de van der Waerden[115] - [116] est popularisée pour l'utilisation de spineurs à deux composantes (spineurs de Weyl (en)) en quatre dimensions d'espace-temps. Arend Heyting introduit l'algèbre de Heyting et l'arithmétique de Heyting (en).
La flèche horizontale → est utilisée pour les fonctions en 1936 par Øystein Ore pour désigner les images d'éléments spécifiques[note 68] - [note 69]. Il écrit pour la première fois en 1940 la forme courante de nos jours, soit f : X → Y, à travers le travail de Witold Hurewicz. Werner Heisenberg, en 1941, propose la théorie de la matrice S (en), d'interactions entre particules.
La notation bra-ket (ou notation de Dirac) est une notation standard pour décrire les états quantiques, composé de crochets et de barres verticales. Elle est aussi utilisée pour les vecteurs abstraits et les formes linéaires. Elle est notée ainsi car le produit scalaire (ou produit hermitien dans un espace vectoriel complexe) de deux états est notée ⟨bra|ket⟩, soit , consistant en une partie gauche, ⟨φ|, et une partie droite, |ψ⟩. La notation a été introduite en 1939 par Paul Dirac[117], même si, 100 ans auparavant, Hermann Grassmann utilisait la notation [φ|ψ] pour le produit scalaire[118].
La notation bra-ket est répandue en mécanique quantique : presque tous les phénomènes expliqués à l'aide de la mécanique quantique, y compris une grande partie de la physique moderne, sont généralement expliqués à l'aide de la notation bra-ket. La notation établit une indépendance de représentation abstraite codée, produisant une représentation spécifique polyvalente (par exemple, x, ou p, ou une base de fonctions propres) sans trop de contexte, ou un recours excessif à la nature des espaces vectoriels impliqués. L'expression de chevauchement ⟨φ|ψ⟩ est généralement interprétée comme l'amplitude de probabilité pour l'état ψ se réduit en l'état ϕ. La notation de barre oblique de Feynman (en) (notation de barre oblique de Dirac[119]) est développée par Richard Feynman pour l'étude des champs de Dirac (en) en théorie quantique des champs.
En 1948, Valentine Bargmann et Eugene Wigner proposent les équations de Bargmann-Wigner (en) relativistes (en) pour décrire les particules libres (en) et les équations sont dans la forme de fonctions propres de champs de spineurs à multi-composantes. En 1950, WIlliam Hodge présente The topological invariants of algebraic varieties dans Proceedings of the International Congress of Mathematicians. Entre 1954 et 1957, Eugenio Calabi travaille sur la conjecture de Calabi (en) pour les Variétés kählériennes et le développement de variétés de Calabi-Yau. En 1957, Tullio Regge formule la propriété mathématique de diffraction potentielles dans l'équation de Schrödinger[note 70] Stanley Mandelstam, avec Regge, fait le développement initial de la théorie de Regge (en) de la phénoménologie d'interaction forte. En 1958, Murray Gell-Mann et Richard Feynman, avec George Sudarshan et Robert Marshak, déduisent les structures chirales de l'interaction faible en physique. Geoffrey Chew, entre autres, promeut la notation matricielles pour l'interaction forte, et le principe bootstrap associé, en 1960. Dans les années 1960, la notation constructeur d'ensemble (en) a été développé pour décrire un ensemble en décrivant les propriétés que ses membres doivent satisfaire. Dans la même période, les tenseurs sont abstraits dans la théorie des catégories aux moyens du concept de la catégorie monoïdale. Plus tard, la notation multi-indicielle élimine des notions conventionnelles utilisées en analyse multivariée, l'étude des équations aux dérivées partielless, et la théorie des distributions, en étendant le concept d'un indice entier à un tuple ordonné d'indices.
Notation mathématique moderne
Dans les mathématiques modernes de la relativité restreinte, l'électromagnétisme et la théorie des ondes, l'opérateur d'alembertien , aussi appelé d'Alembertien ou opérateur d'onde, est l'opérateur laplacien sur un espace de Minkowski. Le symbole de Levi-Civita (ou symbole de permutation, symbole antisymétrique ou symbole alternant) est utilisée en analyse tensorielle.
Après les formulations complètes de la covariance de Lorentz qui étaient finies à tout ordre dans une série de perturbation d'électrodynamique quantique, Sin-Itiro Tomonaga, Julian Schwinger et Richard Feynman ont reçu un prix Nobel de physique commun en 1965[120]. Leurs contributions, et celles de Freeman Dyson, touchent les formulations d'invariance de jauge et covariants de jauge d'électrodynamique quantique qui permettent les calculs d'observables à tout ordre de théorie de la perturbation. La technique mathématique de Feynman, basée sur ses diagrammes, semble de prime abord très différente de l'approche basée sur les opérateurs pour des champs théoriques, de Schwinger et Tomonaga, mais Dyson montre plus tard que les deux approches sont équivalentes. La renormalisation, le besoin d'attacher un sens physique à certaines divergences apparaissant dans la théorie par des intégrales, est devenu par la suite un des aspects fondamentaux de la théorie quantique des champs et devenu un critère d'acceptabilité générale de la théorie. L'électrodynamique quantique a servi de modèle pour les théories quantiques des champs qui ont suivi. Peter Higgs, Jeffrey Goldstone et autres, Sheldon Glashow, Steven Weinberg et Abdus Salam ont montré indépendamment comment la force nucléaire faible et l'électrodynamique quantique peuvent être réunis en une unique force électrofaible. À la fin des années 1960, le zoo de particules (en) est composé des particules élémentaires connues alors, avant la découverte des quarks.
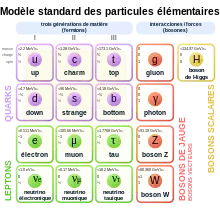
Les fermions fondamentaux et les bosons fondamentaux. (c.2008)[note 71].
Une avancée vers le modèle standard a été la découverte de Sheldon Glashow, en 1960, d'un moyen de combiner les interactions électromagnetique et faible[121]. En 1967, Steven Weinberg[122] et Abdus Salam[123] ajoute le mécanisme de Higgs[124] - [125] - [126] dans la théorie électrofaible de Glashow, lui donnant sa forme moderne. Le mécanisme de Higgs devait accroitre la masse de toutes les particules élémentaires dans le Modèle standard. Il inclut les masses des bosons W et et Z, et les masses des fermions - i.e. les quarks et les leptons. De même en 1967, Bryce DeWitt publie son équation sous le nom d'"équation d'Einstein-Schrödinger" (renommée plus tard "équation de Wheeler-DeWitt")[127]. En 1969, Yoichiro Nambu, Holger Bech Nielsen et Leonard Susskind décrivent l'espace et le temps en termes de cordes. En 1970, Pierre Ramond développe les supersymétries bidimensionnelles. Michio Kaku et Keiji Kikkawa (en) formuleront plus tard les variations de cordes. En 1972, Michael Artin, Alexandre Grothendieck et Jean-Louis Verdier proposent l'univers de Grothendieck[128].
Après que les courants neutres faibles (en) causés par l'échange de bosons Z ont été découverts au CERN en 1973[129] - [130] - [131] - [132], la théorie électrofaible est devenue largement acceptée et Glashow, Salam et Weinberg reçoivent le prix Nobel de physique pour sa découverte. La théorie de l'interaction forte, qui a été le travail de plusieurs contributeurs, acquiert sa forme moderne vers 1973-74. Avec l'établissement de la chromodynamique quantique, un ensemble finalisé de particules fondamentales et d'échange, qui permet l'établissement d'un "modèle standard" basé sur les mathématiques d'une invariance de jauge, qui décrivent avec succès toutes les forces sauf la gravité, et qui reste généralement applicable dans les domaines pour lesquels il a été pensé. À la fin des années 1970, William Thurston introduit la géométrie hyperbolique dans l'étude des nœuds avec le théorème d'hyperbolisation. Le système de notation des orbifolds, inventé par Thurston, a été développée pour représenter les types de groupes de symétrie dans des espaces de dimension 2 à courbure constante. En 1978, Shing-Tung Yau déduit que la conjecture de Calabi (en) a une métrique Ricci-plate (en). En 1979, Daniel Friedan (en) montre que les équations du mouvement de la théorie des cordes sont des abstractions des équations d'Einstein de la relativité générale.
La première révolution des supercordes est composée d'équations mathématiques développées entre 1984 et 1986. En 1984, Vaughan Jones déduit le polynôme de Jones et ses contributions ultérieures de ceux d'Edward Witten, Maxime Kontsevitch et d'autres, qui révèle des liens profonds entre la théorie des nœuds et les méthodes mathématiques en mécanique statistique et la théorie des champs quantiques. Selon la théorie des cordes, toutes les particules du "zoo de particules" ont un ancêtre commun, soit une corde vibrante. En 1985, Philip Candelas (en), Gary Horowitz (en)[133] Andrew Strominger et Edward Witten publient Vacuum configurations for superstrings[134]. Plus tard, le formalisme des tétrades (en) est introduite comme une approche de la relativité générale qui remplace le choix d'une base de coordonnées (en) par un choix moins restrictif d'une base locale pour le fibre tangent (un ensemble localement défini de quatre champs vectoriels linéairement indépendants appelé tétradetétrade[135]).
Dans les années 1990, Roger Penrose propose une notation graphique (en) (notation de diagramme de tenseur) comme, dans les écritures manuscrites, une représentation visuelle des applications multilinéaires ou tenseurs[136]. Penrose introduit une Notation en indice abstrait[note 72]. En 1995, Edward Witten suggère la théorie M et par conséquent l'utilise pour expliquer certaines dualités observées, initiant la seconde révolution des supercordes[note 73].
.jpg.webp)
John Conway introduit plusieurs notations, comme la notation des flèches chaînées de Conway, la notation des nœuds de Conway (en), et la Notation de Conway des polyèdres. Le système de notation de Coxeter (en) classifie les groupes de symétrie, décrit les angles intérieurs avec les réflexions fondamentales d'un groupe de Coxeter. Elle repose sur une notation entre crochets, avec des modificateurs pour indiquer certains sous-groupes. La notation est nommée après H. S. M. Coxeter et Norman Johnson l'a défini de façon plus compréhensive.
La notation LCF combinatoire, conçue par Joshua Lederberg et étendue par Coxeter et Frucht, a été développé pour la représentation des graphes cubiques hamiltonien[137] - [138]. La notation cyclique est la convention pour écrire une permutation en fonction des cycles qui le constituent[139] - [140]. Elle est aussi appelée notation circulaire et la permutation cyclique ou circulaire[141].
Ordinateurs et notation balisée
En 1931, IBM produit le IBM 601 Multiplying Punch ; c'est une machine électromécanique qui peut lire deux nombres, d'au plus long de 8 chiffres, d'une carte perforée et perforer le résultat sur la même carte[142]. En 1934, Wallace Eckert (en) a utilisé une IBM 601 Multiplying Punch trafiquée pour automatiser la résolution d'équations différentielles[143]. En 1936, Alan Turing publie On Computable Numbers, With an Application to the Entscheidungsproblem[144], corrigé en 1938[145]. John von Neumann, pionnier de la programmation et du calcul numérique[note 74] en 1945, écrit First Draft of a Report on the EDVAC (en) (inachevé). En 1962, Kenneth E. Iverson développe une notation de partie intégrale, qui est devenu le langage de programmation APL, pour la manipulation de tableaux qu'il enseigne à ses élèves, et décrit dans son livre A Programming Language[note 75]. En 1970, Edgar F. Codd propose l'algèbre relationnelle comme un modèle relationnel de données pour les langage de requête de bases de données. En 1971, Stephen Cook publie The complexity of theorem proving procedures[146]. Dans les années 1970 avec l'architecture d'ordinateur, une notation est développée pour la notation des nombres rationnels. Dans la même décennie, la notation Z (comme le langage APL) utilise de nombreux symboles absents du système ASCII, la spécification inclut donc des suggestions pour rendre les symboles de la notation Z en ASCII et en LaTeX. Il y a plusieurs fonctions mathématiques en C (Math.h) et librairies numériques, utilisées en développement de logiciel pour l'exécution de calcul numérique. Ces calculs peuvent être utilisées par des exécutions symboliques (en) ; analyser un programme pour déterminer les entrées entraine l'exécution de chaque partie d'un programme. Mathematica et Sympy sont des exemples de logiciels de calcul basés sur le calcul symbolique.
Futur de la notation mathématique

Dans l'histoire de la notation mathématique, la notation des symboles idéographiques est revenu à ses origines avec l'ascension des systèmes de visualisations numériques. Les notations peuvent être appliquées aux visualisations abstraites, comme le rendu de projections d'une variété de Calabi-Yau. Des exemples de images abstraites qui appartiennent spécifiquement à l'imagination mathématique se trouvent dans l'infographie. Le besoin de tels modèles apparait, par exemple, quand les mesures pour le sujet d'étude sont des variables aléatoires et non des fonctions mathématiques ordinaires.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « History of mathematical notation » (voir la liste des auteurs).
Notes
- ou le Moyen Âge
- De tels caractères, en fait, sont conservés avec peu de modifications dans la numération romaine, dont un compte rendu peut être trouvé dans Philosophy of Arithmetic de John Leslie.
- La théorie des nombres est la branche des mathématiques pures consacrée principalement à l'étude des nombres entiers. Les théoriciens des nombres étudient les nombres premiers ainsi que les propriétés des objets constitués d'entiers (par exemple, les nombre rationnels) ou définis comme des généralisations des nombres entiers (par exemple, les entiers algébriques).
- Ce qui est synthétisé dans l'égalité .
- Magnitude (mathématiques) (en), la taille relative d'un objet ; Magnitude (vecteur), un terme pour la norme d'un vecteur ; Scalaire (mathématiques), une quantité définie uniquement par sa valeur ; Vecteur euclidien, une quantité définie à la fois par sa norme et sa direction ; Ordre de grandeur, la classe d'échelle ayant un rapport de valeur fixe à la classe précédente.
- De la Sphère en mouvement d'Autolycos de Pitane est un autre manuscrit mathématique antique de la même période.
- Proclus, un mathématicien grec qui vécut plusieurs siècles après Euclide, écrit dans son commentaire des Éléments : « Euclide, qui a réuni les Éléments, réunissant plusieurs des théorèmes d'Eudoxe, perfectionnant plusieurs de Théétète, et en apportant des démonstrations irréfutables aux choses qui n'étaient que vaguement prouvées par ses prédécesseurs. ».
- L'expression s'écrirait dans ce système : SS2 C3 x5 M S4 u6.
- tels que la règle, l'équerre, le compas, le niveau à bulle et le fil à plomb
- telles que la roue et l'essieu
- L'aire du carré décrit sur l'hypoténuse d'un triangle rectangle est égale à la somme des aires de les carrés décrits sur les côtés
- Al-Kindi a également introduit la cryptanalyse et l'analyse fréquentielle.
- Quelque chose proche d'une preuve par induction mathématique apparaît dans un livre écrit par Al-Karaji vers 1000 apr. J.-C., qui l'a utilisé pour prouver la formule du binôme de Newton, le triangle de Pascal, et l'intégrale d'une fonction cubique.
- Il est ainsi venu près de trouver une formule générale pour les intégraless des polynômes, mais il n'était pas concerné par les polynômes supérieurs au quatrième degré.
- un livre sur ce qu'il percevait comme des défauts dans les Éléments d'Euclide, en particulier l'axiome des parallèles
- traduit en latin par Robert de Chester
- His own personal use started around 1351.
- Summa de arithmetica, geometria, de proportioni et de proportionalita. Tr. Résumé de l'arithmétique, de la géométrie, de la proportion et de la proportionnalité.
- Une grande partie du travail provient de Piero della Francesca qu'il s'est approprié et a volé.
- C'était un cas particulier des méthodes données plusieurs siècles plus tard par Ruffini et Horner.
- (en) John Napier (trad. du latin par William Rae Macdonald), « The Construction of logarythms », dans The Construction of the Wonderful Canon of Logarithms [« Mirifici logarithmorum canonis descriptio »], Édinbourg et Londres, William Blackwood and sons, (lire sur Wikisource)
- voir Infiniment petit.
- En utilisant les coordonnées cartésiennes sur le plan, la distance entre deux points (x1, y1) et (x2, y 2) est défini par la formule :
qui peut être considéré comme une version du théorème de Pythagore. - Par exemple, le "Problème des partis".
- Par exemple,
- Par exemple, la dérivée de la fonction x serait écrite sous la forme . La dérivée seconde de x s'écrirait , etc.
- Par exemple, le dérivée de la fonction x par rapport à la variable t dans la notation de Leibniz s'écrirait .
- Voir aussi : Représentations de e
- Ainsi dénote le résultat mathématique de l'exécution de l'opération sur le sujet . Si sur ce résultat la même opération était répétée, le nouveau résultat serait exprimé par , ou plus précisément par , et ainsi de suite. La quantité elle-même considérée comme le résultat de la même opération sur une autre fonction ; le symbole approprié pour lequel est, par analogie, . Ainsi et sont des symboles d'opération inverse, le premier annulant l'effet du second sur le sujet . et de la même manière sont appelés réciproque.
- C'est-à-dire
- Aujourd'hui, le symbole créé par John Wallis, , est utilisé pour l'infini
- Comme dans
- la notation sigma majuscule utilise un symbole qui représente de manière compacte la sommation de nombreux termes similaires : le symbole de sommation, Σ, une forme agrandie de la lettre grecque majuscule verticale sigma. Ceci est défini comme :
Où, i représente l'indice de sommation ; ai est une variable indexée représentant chaque terme successif de la série ; m est la borne inférieure de sommation, et n est la borne supérieure de sommation. Le "i = m" sous le symbole de sommation signifie que l'index i commence pour l'indice m. L'indice, i, est incrémenté de 1 pour chaque terme successif, s'arrêtant lorsque i = n. - Il part de l'égalité .
valable pour n > 0. - Le d rond ou delta de Jacobi.
- A propos de la preuve du théorème de Wilson. Disquisitiones arithmeticae (1801) Article 76
- La théorie de Galois et la géométrie de Galois (en) portent son nom.
- C'est-à-dire "sous-ensemble de" et "surensemble de" ; ils seront plus tard redéveloppés par Ernst Schröder.
- Une science des nombres qui utilise des méthodes issues de l'analyse mathématique pour résoudre des problèmes sur les nombres entiers.
- Cité dans (en) Robert Perceval Graves (en), Life of Sir William Rowan Hamilton — 3 volumes : 1882, 1885, 1889.
- Voir Opérateur hamiltonien.
- C'est-à-dire,
- Bien que son utilisation décrive quelque chose de différent de ce que l'on entend maintenant par un tenseur. À savoir, la norme dans un certain type de système algébrique (maintenant connu sous le nom d'algèbre de Clifford).
- C'est-à-dire
où - Dérivé de Matrix, le mot latin pour "utérus".
- C'est-à-dire,
- Clifford a réuni l'algèbre avec les quaternions de Hamilton en remplaçant la règle de Hermann Grassmann epep = 0 par la règle epep = 1. Pour plus de détails, voir algèbre extérieure.
- Voir : Phaseur, Groupe (mathématiques), Propagation des ondes, Vitesse d'une onde Phase (électricité), oscillateur harmonique et Circuit RLC
- Ou le concept d'un quatrième dimension spatiale. Voir aussi : espace-temps, l'unification du temps et de l'espace en tant que continuum à quatre dimensions ; et, espace de Minkowski, le cadre mathématique de la relativité restreinte.
- Voir aussi : Corps commutatif et extension de corps
- Cela soulève des questions sur le théorèmes d'existence pure.
- L'arithmétique transfinie est la généralisation de l'arithmétique élémentaire à l'infini des quantités comme les ensembles infinis ; Voir Nombre transfini, Induction transfinie et interpolation transfinie (en). Voir aussi Opérations arithmétiques sur les ordinaux.
- Dans cet article Steinitz a étudié axiomatiquement les propriétés des corps et a défini de nombreux concepts théoriques de corps importants comme le corps premier, le corps parfait et le degré de transcendance d'une extension de corps.
- Les indices parcourent l'ensemble {1, 2, 3,
Voir aussi : Tenseur de Ricci - La théorie du tenseur de Ricci pose les règles de notation indicielle et de manipulation pour les tenseurs et Champs tensoriels. Voir aussi : (en) J. L. Synge et A. Schild, Tensor Calculus, first Dover Publications, (1re éd. 1949), p. 6-108.
- Ici une constante logique est un symbole en logique symbolique qui a la même signification dans tous les modèles, comme le symbole "=" pour "égal".
Une constante, dans un contexte mathématique, est un nombre qui apparaît naturellement en mathématiques, tel que π ou e ; Une telle constante mathématique ne change pas. Cela peut signifier le coefficient constant d'un polynôme (le terme de degré 0) ou la constante d'intégration (en), un paramètre libre apparaissant dans l'intégration.
En relation, les constantes physiques sont une physique quantité généralement considérée comme universelle et immuable. Les constantes de programmation sont des valeurs qui, contrairement à une variable, ne peuvent pas être réassociées à une valeur différente. - Bien qu'il ne s'agisse pas d'un terme d'indexation, les mots-clés sont des termes qui représentent des informations. Un mot-clé est un mot avec une signification particulière (c'est une définition sémantique), alors que syntaxiquement ce sont des symboles terminaux dans la grammaire de la phrase.
- La plupart de ces symboles peuvent être trouvés dans le calcul des propositions, un système formel décrit comme . est l'ensemble des éléments, comme le a dans l'exemple avec l'algèbre booléenne ci-dessus. est l'ensemble qui contient les sous-ensembles qui contiennent des opérations, telles que ou . contient les règles d'inférence, qui sont les règles dictant comment les inférences peuvent être logiquement faites, et contient les axiomes. Voir aussi : Formes normales conjonctives, formes normales disjonctives.
- Usuellement notés par x, y, z, ou toute autre lettre minuscule. Ici un symbole qui représente une quantité dans une expression mathématique, une variable mathématique telle qu'utilisée de plusieurs sciences.
Des variables peuvent être des noms symboliques associées à une valeur, et celles-ci peuvent être changées ; c'est ce qu'on appelle une variable référence. Une variable peut aussi être le moyen opérationalisée dans lequel l'attribut est représenté pour du traitement de données (e.g., un ensemble logique d'attributs). Voir aussi : Variables dépendantes et indépendantes (en) en statistiques. - par ex. ∃ pour "il existe" et ∀ pour "pour tout"
- Voir aussi : Dialethéisme, Contradiction, et Paradoxe
- Voir facetious abstract nonsense décrit certains types d'arguments et de méthodes liés à la théorie des catégories qui ressemble à comique dispositifs non séquentiels littéraires (pas illogical non-sequiturs).
- Les Théorèmes d'incomplétude de Gödel montrent que le programme de Hilbert pour trouver un ensemble d'axiomes complet et cohérent pour toutes les mathématiques est impossible, donnant une réponse négaitve au deuxième problème de Hilbert
- L'équation de Klein-Gordon est :
- L'équation de Dirac dans le forme initialement proposée par Dirac est :
où, ψ = ψ(x, t) est le fonction d'onde pour l'électron, x et t sont les coordonnées spatiales et temporelles, m est la masse au repos de l'électron, p est l'impulsion, comprise comme l'opérateur d'impulsion (en) dans l'théorie de Schrödinger, c est la vitesse de la lumière, et ħ = h/2π est la constante de Planck réduite. - Soit
- Le théorème s'applique plus généralement à tout système formel suffisamment fort, montrant que la vérité dans le modèle standard de le système ne peut pas être défini dans le système.
- Voir la correspondance de Galois.
- Øystein Ore écrit aussi (en) Number Theory and Its History, New York, McGraw-Hill, (OCLC 1222245278, lire en ligne).
- Elle dit que l'amplitude de diffraction peut être pensée dans une fonction analytique du moment angulaire, et que la position des pôles déterminent les taux de croissance de l'amplitude dans la région purement mathématique de grandes valeurs du cosinus de l'angle de diffractione.
- Notons que les "masses" (e.g., les formes des corps cohérentes non définies) de particules
 sont périodiquement réévaluées par la communauté scientifique. Les valeurs peuvent être ajustées ; l'ajustement par des opérations menées par des instruments afin d'obtenir des indications voulues correspondant aux valeurs données du mesurande. En ingénierie, mathématiques et géodésie, le paramètre
sont périodiquement réévaluées par la communauté scientifique. Les valeurs peuvent être ajustées ; l'ajustement par des opérations menées par des instruments afin d'obtenir des indications voulues correspondant aux valeurs données du mesurande. En ingénierie, mathématiques et géodésie, le paramètre  optimal d'une telle estimation d'un modèle mathématique doit approcher au mieux un jeu de données.
optimal d'une telle estimation d'un modèle mathématique doit approcher au mieux un jeu de données. - Son usage de la sommation d'Einstein avait pour but de réduire l'inconvénient de décrire les contractions et la dérivation covariante en notation tensorielle abstraire moderne, tout en maintenant une covariance explicite des expressions utilisées.
- Voir paysage de la théorie des cordes (en) and Marécage (physique)
- Parmi les autres contributions de von Neumann, on compte l'application de la théorie des opérateurs (en) à la mécanique quantique, le développement de l'analyse fonctionnelle, et plusieurs formes de la théorie des opérateurs.
- (en) Kenneth E. Iverson, A programming language, New York, Wiley, (OCLC 489884069).
Références et citations
- Cajori 2011.
- (en) William Thomas Brande (éd.) et George William Cox (en), A Dictionary of Science, Literature, & Art, vol. 2, Longmans, Green and Company, (lire en ligne), p. 683.
- (en) Eric W. Weisstein, « Notation », sur MathWorld.
- (en) Sir Thomas Little Heath, Diophantos of Alexandria: A Study in the History of Greek Algebra, University Press, (lire en ligne), p. 77.
- (en) Karl J. Smith, Mathematics: Its Power and Utility, Cengage Learning, , 9e éd. (lire en ligne), p. 86.
- (en) Warren Van Egmond, The Commercial Revolution and the Beginnings of Western Mathematics in Renaissance Florence, 1300-1500, (OCLC 5894519971), p. 233.
- (en) Solomon Gandz (en), « The Sources of al-Khowarizmi's Algebra », Osiris, vol. 1, , p. 263-277.
- (en) Thomas Gamaliel Bradford, Encyclopædia Americana, Desilver, Thomas, & Company, (lire en ligne), p. 314.
- (en) Richard N. Aufmann, Joanne Lockwood, Richard D. Nation et Daniel K. Clegg, Mathematical Excursion, Enhanced Edition, Cengage Learning, (lire en ligne), p. 186.
- (en) C. B. Boyer et Uta C. Merzbach (rév.), « Mesopotamia », dans A History of Mathematics, New York, Wiley, , 2e éd. (ISBN 0-471-09763-2 et 0-471-54397-7, OCLC 1244458613), p. 25.
- (en) Asger Aaboe, Episodes from the Early History of Mathematics, Washington D. C., The Mathematical Association of America, coll. « New mathematical library », (ISBN 9780883856130, OCLC 716281303), p. 30-31.
- (en) Heath, « A Manual of Greek Mathematics », Nature, vol. 128, no 3235, , p. 5 (DOI 10.1038/128739a0, Bibcode 1931Natur.128..739T, S2CID 3994109).
- (en) Sir Thomas L. Heath, A Manual of Greek Mathematics, New York, Dover, (OCLC 5894429800), p. 1
- « In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who made mathematics a science. ».
- (en) The new encyclopædia; or, Universal dictionary of arts and sciences, Encyclopædia Perthensis, p. 49.
- (en) Ronald Calinger, Joseph E. Brown et Thomas R. West, A contextual history of mathematics : to Euler, Prentice-Hall, (ISBN 0023182857), p. 150
- « Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity. ».
- (en) John J. O'Connor et Edmund F. Robertson, « Archimedes of Syracuse », sur MacTutor, université de St Andrews, (consulté le ). .
- (en) John J. O'Connor et Edmund F. Robertson, « A history of the calculus », sur MacTutor, université de St Andrews, (consulté le ). .
- (en) -, « Proclus and the history of geometry as far as Euclid », sur MacTutor, université de St Andrews, (consulté le ). .
- (en) John Caldwell, « De Institutione Arithmetica, De Institutione Musica », dans Margaret Gibson (éd.), Boethius: His Life, Thought, and Influence, Oxford, Blackwell, (ISBN 9780631111412, OCLC 461855853).
- (de) Menso Folkerts, "Boethius" Geometrie II, Wiesbaden, Franz Steiner Verlag, (OCLC 5894487134).
- (en) Oswald Ashton Wentworth Dilke, Mathematics and Measurement, University of California Press, coll. « Reading the past » (no 2), (ISBN 9780520060722, lire en ligne), p. 14.
- (en) W.T. Brande et G. W. Cox, A dictionary of science, literature and art, vol. 2, Longmans, Green, and Company, (lire en ligne), p. 683.
- Jean-Baptiste Joseph Delambre, Histoire de l'astronomie ancienne, t. ii, Courcier, (OCLC 872415522).
- (en) Carl B. Boyer, A History of Mathematics, John Wiley & Sons, Inc., , 2e éd..
- (en) Aaron Zerhusen, Chris Rakes, Shasta Meece et Dr. Carl Eberhart (rév.), « Diophantine Equations », sur le site du College of Arts and Sciences de l'université du Kentucky, .
- (en) Sir Thomas Little Heath, A History of Greek Mathematics: From Aristarchus to Diophantus, Oxford, Clarendon Press, (lire en ligne).
- (en) Charles E. Woodruff, « The Evolution of Modern Numerals from Ancient Tally Marks », The American Mathematical Monthly, vol. 16, nos 8/9, , p. 125-133 (DOI 10.2307/2970818, JSTOR 2970818).
- (en) John J. O'Connor et Edmund F. Robertson, « Overview of Chinese mathematics », sur MacTutor, université de St Andrews, (consulté le ). .
- (en) George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Londres, Penguin Books, (ISBN 9780140125290, OCLC 802923206), p. 140—148.
- (de) Georges Ifrah, Universalgeschichte der Zahlen, Francfort/New York, Campus, (ISBN 9783593336664, OCLC 46083164), p. 428—437.
- (en) Frank J. Swetz et T. I. Kao, « Was Pythagoras Chinese? », sur le site de Penn State University Press (consulté le ).
- (en) Joseph Needham, Science and Civilization in China, vol. 3 : Mathematics and the Sciences of the Heavens and the Earth, Cambridge, University Press, (1re éd. 1959) (ISBN 9780521058018, OCLC 257106241).
-
(en) C. B. Boyer et Uta C. Merzbach (rév.), « China and India », dans A History of Mathematics, New York, Wiley, , 2e éd. (ISBN 0-471-09763-2 et 0-471-54397-7, OCLC 1244458613), p. 25
- « he was the first one to give a general solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. [...] It is greatly to the credit of Brahmagupta that he gave all integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India - or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words. »
- (en) Robert Kaplan, The Nothing That Is: A Natural History of Zero, Londres, Allen Lane/The Penguin Press, (ISBN 9780140279436, OCLC 44485042)
- (en) John J. O'Connor et Edmund F. Robertson, « Indian numerals », sur MacTutor, université de St Andrews.
- « The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius. »
- (de) Adolf Yushkevich, Geschichte der Mathematik im Mittelalter, Leipzig, Teubner, .
- (en) C. B. Boyer et Uta C. Merzbach (rév.), « The Arabic Hegemony », dans A History of Mathematics, New York, Wiley, , 2e éd. (ISBN 0-471-09763-2 et 0-471-54397-7, OCLC 1244458613)
- « The six cases of equations given above exhaust all possibilities for linear and quadratic equations having positive root. So systematic and exhaustive was al-Khwārizmī's exposition that his readers must have had little difficulty in mastering the solutions. ».
- (en) Gandz et Saloman, The sources of Khwarizmi's algebra, Osiris i, , p. 263-77
- « In a sense, Khwarizmi is more entitled to be called « the father of algebra » than Diophantus because Khwarizmi is the first to teach algebra in an elementary form and for its own sake, Diophantus is primarily concerned with the theory of numbers ».
- (en) C. B. Boyer et Uta C. Merzbach (rév.), « The Arabic Hegemony », dans A History of Mathematics, New York, Wiley, , 2e éd. (ISBN 0-471-09763-2 et 0-471-54397-7, OCLC 1244458613)
- « It is not certain just what the terms al-jabr and muqabalah mean, but the usual interpretation is similar to that implied in the translation above. The word al-jabr presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word muqabalah is said to refer to "reduction" or "balancing" - that is, the cancellation of like terms on opposite sides of the equation. ».
- (en) R. Rashed et Angela Armstrong, The Development of Arabic Mathematics, Springer, (ISBN 0-7923-2565-6, OCLC 29181926), p. 11-12.
- (en) Victor J. Katz, History of Mathematics: An Introduction, Addison-Wesley, (ISBN 0-321-01618-1), p. 255-259.
- Franz Woepcke, Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi, Paris, Imprimerie impériale, (OCLC 1179467225).
- (en) Victor J. Katz, « Ideas of Calculus in Islam and India », Mathematics Magazine, vol. 68, no 3, , p. 163-74 (DOI 10.1080/0025570X.1995.11996307).
- (en) Paul Kunitzsch et A. I. Sabra, The Enterprise of Science in Islam: New Perspectives, J. P. Hogendijk, (ISBN 978-0-262-19482-2, lire en ligne), « The Transmission of Hindu-Arabic Numerals Reconsidered », p. 3-22 (12-13).
- (en) Marie-Thérèse d'Alverny, « Translations and Translators », dans Robert L. Benson et Giles Constable, Renaissance and Renewal in the Twelfth Century, Cambridge, Harvard University Press, , p. 421-462.
- (en) Guy Beaujouan, « The Transformation of the Quadrivium », dans Robert L. Benson et Giles Constable, Renaissance and Renewal in the Twelfth Century, Cambridge, Harvard University Press, , p. 463-487.
- (en) John J. O'Connor et Edmund F. Robertson, « al-Marrakushi ibn Al-Banna », sur MacTutor, université de St Andrews. .
- (en) Jan Gullberg (en), Mathematics: From the Birth of Numbers, W. W. Norton, (ISBN 0-393-04002-X, lire en ligne), p. 298.
- (en) John J. O'Connor et Edmund F. Robertson, « Abu'l Hasan ibn Ali al Qalasadi », sur MacTutor, université de St Andrews. .
- (en) C. B. Boyer et Uta C. Merzbach (rév.), « Revival and Decline of Greek Mathematics », dans A History of Mathematics, New York, Wiley, , 2e éd. (ISBN 0-471-09763-2 et 0-471-54397-7, OCLC 1244458613), p. 178
- « The chief difference between Diophantine syncopation and the modern algebraic notation is the lack of special symbols for operations and relations, as well as of the exponential notation. ».
- (en) Edward Grant (éd.) et John E. Murdoch (éd.), Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, Cambridge, Cambridge University Press, (ISBN 0-521-32260-X).
- (en) Artemas Martin, Mathematical Magazine, vol. 1, (lire en ligne), p. 124
- (de) Nicole Oresme, Der Algorismus proportionum des Nicolaus Oresme : Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn, Druck von J. Draeger's buchdruckerei (C. Feicht), (lire en ligne).
- (en) Michael Walsh, A New System of Mercantile Arithmetic : Adapted to the Commerce of the United States, in Its Domestic and Foreign Relations with Forms of Accounts and Other Writings Usually Occurring in Trade, Edmund Blunt (en), (présentation en ligne).
- (en) Anne Rooney, The History of Mathematics (lire en ligne), p. 40
- (en) Mark Napier, Memoirs of John Napier of Merchiston, Edinburgh, W. Blackwood, (lire en ligne)
- (en) David Stewart Erskine, comte de Buchan et Walter Minto, An Account of the Life, Writings, and Inventions of John Napier, of Merchiston, (lire en ligne)
- Florian Cajori, Une histoire des mathématiques, Macmillan, (lire en ligne), p. 157.
- (en) Jan Gullberg (en), Mathematics: From the Birth of Numbers, W. W. Norton, , p. 963-965
- (la) William Jones, Synopsis Palmariorum Matheseos, (présentation en ligne).
- (en) By Claudi Alsina et Roger B. Nelse, When Less is More: Visualizing Basic Inequalities (lire en ligne), p. 18.
- (la) Leonhard Euler, « Solutio problematis ad geometriam situs relevantis », Commentarii academiae scientiarum Petropolitanae, vol. 8, , p. 128-140 (lire en ligne).
- (en) William Emerson, The elements of geometry, (lire en ligne).
- (en) William Emerson, The Doctrine of Proportion, Arithmetical and Geometrical. Together with a General Method of Arening by Proportional Quantities, (présentation en ligne)
- (en) George Baron, The Mathematical Correspondent, vol. 1, Sage and Clough,, (lire en ligne), p. 83
- (en) Marie A. Vitulli, « A Brief History of Linear Algebra and Matrix Theory », sur le site du Département de mathématiques de l'Université de l'Oregon (version du 10 septembre 2012 sur Internet Archive).
- (en) John J. O'Connor et Edmund F. Robertson, « Christian Kramp », sur MacTutor, université de St Andrews, (consulté le ). .
- Joseph-Louis Lagrange, Mécanique analytique (1re éd. 1788) — 2 volumes
Tome premier, Paris, Mallet-Bachelier, , 3e éd. (lire en ligne)Tome second, Paris, Mallet-Bachelier, , 3e éd. (lire en ligne)
- (en) Arthur Cayley, The collected mathematical papers of Arthur Cayley, vol. 11 (lire en ligne), p. 243.
- (en) Ari Ben-Menahem, Historical Encyclopedia of Natural and Mathematical Sciences, vol. 1 (lire en ligne), p. 2070.
- (en) Marie A. Vitulli, « A Brief History of Linear Algebra and Matrix Theory » [PDF].
- (en) Steven Schwartzman, The Words of Mathematics (lire en ligne), p. 6.
- (en) A. Pramanik, Electro-Magnetism: Theory and Applications, Prentice Hall India Pvt., (lire en ligne), p. 38.
- (en) Arnold Neumaier, « History of Nabla and Other Math Symbols », sur le blog homepages.math.uic.edu, (consulté le ).
- (en) William Rowan Hamilton, « On some Extensions of Quaternions », Philosophical Magazine, David R. Wilkins, nos 7–9, 1854-1855, p. 492-499, 125-137, 261-269, 46-51, 280–290 (ISSN 0302-7597, lire en ligne).
- (en) « James Clerk Maxwell », sur IEEE Global History Network (consulté le ).
- (en) James Clerk Maxwell, « A Dynamical Theory of the Electromagnetic Field », Philosophical Transactions of the Royal Society of London, vol. 155, , p. 459–512 (DOI 10.1098/rstl.1865.0008, Bibcode 1865RSPT..155..459C, S2CID 186207827).Cet article accompagnait une présentation du 8 décembre 1864 par Maxwell à la Royal Society.
- disponible sur Internet Archive ; disponible sur Internet Archive.
- (en) David A. Cox, Galois Theory, vol. 106, Hoboken, NJ, John Wiley & Sons, coll. « Pure and Applied Mathematics », , 2e éd. (ISBN 978-1118218426, OCLC 784952441), p. 348.
- (en) Hussein Tevfik (Pacha.), Linear Algebra, Constantinople, A. H. Boyajian, (OCLC 493424867, lire en ligne).
- G. Ricci Curbastro, « Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique », Bulletin des Sciences Mathématiques, vol. 2, no 16, , p. 167–189.
- (de) Woldemar Voigt, Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung, Leipzig, Von Veit, (OCLC 3196683, lire en ligne).
- (en) Henri Poincaré, « Analysis situs », Journal de l'École Polytechnique, 2e série, vol. 1, , p. 1–123.
- (en) Charles Proteus Steinmetz, Theory and calculation of alternating current phenomena [« Théorie et calcul des phénomènes de courant alternatif »], , 3e éd. (1re éd. 1895) (présentation en ligne)
- John B. Whitehead Jr., « Review: Alternating Current Phenomena, by C. P. Steinmetz », Bull. Amer. Math. Soc., vol. 7, no 9, , p. 399–408 (DOI 10.1090/s0002-9904-1901-00825-7, lire en ligne).
-
Parmi les nombreuses éditions, on en considère deux :
- (fr) Giuseppe Peano, Formulaire des mathématiques, Paris, Gauthier-Villars, , 230 p. (présentation en ligne, lire en ligne)
- (it) Giuseppe Peano, Formulario mathematico, Rome, Edizione cremonese, , 463 p. (présentation en ligne).
- Gregorio Ricci-Curbastro et Tullio Levi-Civita, « Méthodes de calcul différentiel absolu et leurs applications », Mathematische Annalen, Springer, vol. 54, nos 1–2, , p. 125–201 (DOI 10.1007/BF01454201, S2CID 120009332, lire en ligne).
- (de) Ernst Zermelo, « Beweis, dass jede Menge wohlgeordnet werden kann », Mathematische Annalen, vol. 59, no 4, , p. 514–16 (DOI 10.1007/BF01445300, S2CID 124189935).
- Sur la dynamique de l’électron (Wikisource)
- Maurice Fréchet, Sur quelques points du calcul fonctionnel (thèse de doctorat), Paris, École normale supérieure,
- (en) Cuthbert Edmund Cullis (en), Matrices and determinoids, vol. 2, Cambridge University Press, (ISBN 9781107620834).
- (de) Issai Schur, Über eine Klasse von Matrizen, die sich einer gegebenen Matrix zuordnen lassen [« Sur une classe de matrices à laquelle peut appartenir une matrice donnée »], Université Harvard, , 74 p. (présentation en ligne)
- (en) Florian Cajori, An Introduction To The Modern Theory Of Equations, New York, Londres, The Macmillan company, (lire en ligne).
- Proceedings of the Prussian Academy of Sciences (1918). Pg 966.
- (de) Sitzungsberichte der Preussischen Akademie der Wissenschaften [« Actes de l'Académie prussienne des sciences »], (lire en ligne)
- Théorie de Kaluza-Klein
- (en) Charles Proteus Steinmetz, Four lectures on relativity and space, New York, McGraw-Hill, (lire en ligne).
- (en) J.A. Wheeler, C. Misner et K.S. Thorne, Gravitation, W.H. Freeman & Co, (ISBN 0-7167-0344-0, lire en ligne), p. 85–86 §3.5.
- (en) R. Penrose, The Road to Reality [« À la découverte des lois de l'univers : La prodigieuse histoire des mathématiques et de la physique »], Vintage books, (1re éd. 2004) (ISBN 978-0-679-77631-4).
- (de) Jan A. Schouten, Der Ricci-Kalkül [« Le calcul de Ricci »], Berlin, R. Courant, Springer Verlag, coll. « Grundlehren der mathematischen Wissenschaften » (no 10), (lire en ligne).
- (en) Robert B. Ash, A Primer of Abstract Mathematics, Cambridge University Press, (lire en ligne).
- (en) J.A. Hill, The New American Encyclopedic Dictionary, Edward Thomas Roe, Le Roy Hooker, Thomas W. Handford (lire en ligne), p. 34.
- (en) Sir Isaac Newton et John Machin, The Mathematical Principles of Natural Philosophy, vol. 1.
- (en) Bertrand Russel, The Scientific Outlook, Londres, G. Allen and Unwin, (OCLC 491031572).
- (en) Thomas Fisher, Mathematics simplified and made attractive: or, The laws of motion explained, p. 15 :
- « But an abstraction not founded upon, and not consonant with Nature and (Logical) Truth, would be a falsity, an insanity. »
- « Mais une abstraction non fondée sur, et non conforme à la Nature et à la Vérité (Logique), serait une fausseté, une folie. »
- Traduction de la Proposition VI, dans l'article (de) Kurt Gödel, « Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (en) », Monatshefte für Mathematik,
- (en) John L. Casti, 5 Golden Rules : great theories of 20th-century mathematics and why they matter, New York, MJF Books, (ISBN 9781567317084, OCLC 58846711)
- (de) David Hilbert et Richard Courant, Methoden der mathematischen Physik [« Méthodes de physique mathématique »], Berlin, Verlag von Julius Springer, — 2 volumes.
- (en) P.A.M. Dirac, « The Quantum Theory of the Emission and Absorption of Radiation », Proceedings of the Royal Society, vol. 114, no 767, , p. 243-265 (DOI 10.1098/rspa.1927.0039, Bibcode 1927RSPSA.114..243D).
- (en) Enrico Fermi, « Quantum Theory of Radiation », Reviews of Modern Physics, vol. 4, no 1, , p. 87-132 (DOI 10.1103/RevModPhys.4.87, Bibcode 1932RvMP....4...87F).
- (en) Félix Bloch et Arnold Nordsieck (en), « Note on the Radiation Field of the Electron », Physical Review, vol. 52, no 2, , p. 54-59 (DOI 10.1103/PhysRev.52.54, Bibcode 1937PhRv...52...54B).
- (en) « On the Self-Energy and the Electromagnetic Field of the Electron », Physical Review, vol. 56, no 1, , p. 72-85 (DOI 10.1103/PhysRev.56.72, Bibcode 1939PhRv...56...72W).
- (en) Robert Oppenheimer, « Note on the Theory of the Interaction of Field and Matter », Physical Review, vol. 35, no 5, , p. 461-477 (DOI 10.1103/PhysRev.35.461, Bibcode 1930PhRv...35..461O).
- Kurt Gödel, « The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis », Proceedings of the National Academy of Sciences of the United States of America, vol. 24, no 12, , p. 556 (PMID 16577857, DOI 10.1073/pnas.24.12.556).
- (de) B. L. Van der Waerden, « Spinoranalyse », Nachr. Ges. Wiss. Göttingen Math.-Phys., vol. 1929, , p. 100-109.
- (en) O. Veblen, « Geometry of two-component Spinors », Proc. Natl. Acad. Sci. USA, vol. 19, no 4, , p. 462-474 (PMID 16577541, PMCID 1086023, DOI 10.1073/pnas.19.4.462, Bibcode 1933PNAS...19..462V).
- (en) Paul Dirac, « A new notation for quantum mechanics », Mathematical Proceedings of the Cambridge Philosophical Society, vol. 35, no 3, , p. 416-418 (DOI 10.1017/S0305004100021162, Bibcode 1939PCPS...35..416D, S2CID 121466183)
- Hermann Graßmann (trad. de l'allemand), La science de la grandeur extensive : la « Lineale Ausdehnungslehre » [« Die lineale Ausdehnungslehre »], Paris, A. Blanchard, coll. « Sciences dans l'histoire », (1re éd. 1844) (ISBN 9782853671903, OCLC 258354683).
- (en) Steven Weinberg, The quantum theory of fields, vol. 2, Cambridge University Press, (1re éd. 1964) (ISBN 0-521-55001-7, lire en ligne), p. 358.
- (en) « The Nobel Prize in Physics 1965 », Nobel Foundation (consulté le ).
- (en) S.L. Glashow, « Partial-symmetries of weak interactions », Nuclear Physics, vol. 22, no 4, , p. 579-588 (DOI 10.1016/0029-5582(61)90469-2, Bibcode 1961NucPh..22..579G).
- (en) S. Weinberg, « A Model of Leptons », Physical Review Letters, vol. 19, no 21, , p. 1264-1266 (DOI 10.1103/PhysRevLett.19.1264, Bibcode 1967PhRvL..19.1264W).
-
(en) A. Salam et N. Svartholm (éd.) « Elementary Particle Physics: Relativistic Groups and Analyticity » ()
—8e symposium Nobel. -
(en) F. Englert et R. Brout, « Broken Symmetry and the Mass of Gauge Vector Mesons », Physical Review Letters, vol. 13, no 9, , p. 321-323 (DOI 10.1103/PhysRevLett.13.321
 , Bibcode 1964PhRvL..13..321E).
, Bibcode 1964PhRvL..13..321E). -
(en) P.W. Higgs, « Broken Symmetries and the Masses of Gauge Bosons », Physical Review Letters, vol. 13, no 16, , p. 508-509 (DOI 10.1103/PhysRevLett.13.508
 , Bibcode 1964PhRvL..13..508H).
, Bibcode 1964PhRvL..13..508H). -
(en) G.S. Guralnik, C.R. Hagen et T.W.B. Kibble, « Global Conservation Laws and Massless Particles », Physical Review Letters, vol. 13, no 20, , p. 585-587 (DOI 10.1103/PhysRevLett.13.585
 , Bibcode 1964PhRvL..13..585G).
, Bibcode 1964PhRvL..13..585G). - (en) Carlo Rovelli « Notes for a brief history of quantum gravity » () (lire en ligne) [PDF]
—9th Marcel Grossmann Meeting (Rome, ). - Nicolas Bourbaki « Univers » () (lire en ligne)
—Séminaire de géométrie algébrique du Bois Marie
— « (ibid.) », dans Michael Artin, Alexandre Grothendieck et Jean-Louis Verdier (éds.), 1963-64 : Théorie des topos et cohomologie étale des schémas, Berlin, New York, Springer-Verlag (ISBN 978-3-540-05896-0, OCLC 7330933131), p. 185-217. - (en) F.J. Hasert et al., « Search for elastic muon-neutrino electron scattering », Physics Letters B, vol. 46, no 1, , p. 121 (DOI 10.1016/0370-2693(73)90494-2, Bibcode 1973PhLB...46..121H).
- (en) F.J. Hasert et al., « Observation of neutrino-like interactions without muon or electron in the gargamelle neutrino experiment », Physics Letters B, vol. 46, no 1, , p. 138 (DOI 10.1016/0370-2693(73)90499-1, Bibcode 1973PhLB...46..138H).
- (en) F.J. Hasert et al., « Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment », Nuclear Physics B, vol. 73, no 1, , p. 1 (DOI 10.1016/0550-3213(74)90038-8, Bibcode 1974NuPhB..73....1H).
- (en) D. Haidt, « The discovery of the weak neutral currents », sur CERN Courier (en), (consulté le ).
- (en) « Gary Horowitz » (biographie), sur le site de la faculté de Physique de l'université de Californie à Santa Barbara (consulté le ).
- (en) P. Candelas, « Vacuum configurations for superstrings », Nuclear Physics B, vol. 258, , p. 46-74 (DOI 10.1016/0550-3213(85)90602-9, Bibcode 1985NuPhB.258...46C).
- (en) F. De Felice et C. J. S. Clarke, Relativity on curved manifolds, Cambridge University Press, coll. « Cambridge monographs on mathematical physics », (ISBN 9780521429085, OCLC 59243639), p. 133.
- (en) V. G. Turaev, Quantum invariants of knots and 3-manifolds, , p. 71.
- (en) Tomaž Pisanski (en) et Brigitte Servatius (en), « Cubic graphs and LCF notation », dans Configurations from a Graphical Viewpoint, Springer, (ISBN 9780817683641, lire en ligne), p. 32.
- (en) R. Frucht, « A canonical representation of trivalent Hamiltonian graphs », Journal of Graph Theory, vol. 1, no 1, , p. 45-60 (DOI 10.1002/jgt.3190010111).
- (en) John B. Fraleigh, A first course in abstract algebra, Boston, Mass., Addison-Wesley, , 7e éd. (ISBN 9780201763904, OCLC 82363439), p. 89.
- (en) Thomas W. Hungerford, Abstract algebra : an introduction, Fort Worth, Saunders College Publ, , 2e éd. (ISBN 9780030105593, OCLC 833236562), p. 230
- (en) Edgar Dehn, Algebraic Equations, New York, Dover, coll. « Dover books on advanced mathematics » (no 19), (1re éd. 1930).
- (en) « The IBM 601 Multiplying Punch », sur Columbia.edu (version du 14 juillet 2014 sur Internet Archive).
- (en) « Interconnected Punched Card Equipment », sur Columbia.edu, (version du 28 avril 2023 sur Internet Archive).
- (en) Alan Turing, « On Computable Numbers, With an Application to the Entscheidungsproblem », Proceedings of the London Mathematical Society, vol. 42, no 2, (lire en ligne).
- (en) Alan M. Turing, « On Computable Numbers, with an Application to the Entscheidungsproblem. A Correction », Proceedings of the London Mathematical Society, vol. s2-43, , p. 544-546 (DOI 10.1112/plms/s2-43.6.544).
- (en) Stephen Cook, « The complexity of theorem proving procedures », dans Proceedings of the Third Annual ACM Symposium on Theory of Computing, (ISBN 9781450374644, DOI 10.1145/800157.805047, S2CID 7573663), p. 151-158.
Voir aussi
Bibliographie
- Général
- (en) Florian Cajori, A History of Mathematical Notations, New York, Cosimo, (réimpr. 1951, 1974, 1993, 2007, 2015) (1re éd. 1928-1929) (ISBN 0-486-67766-4, OCLC 1183711702) — édition en un volume ; éditions 1928, 1951 et 1974 en 2 volumes :
- Notations in Elementary Mathematics
- Notations mainly in higher mathematics
- (en) Walter William Rouse Ball, A Short Account of the History of Mathematics, Macmillan, (lire en ligne)
- (en) Walter William Rouse Ball, A Primer of the History of Mathematics, Macmillan, (lire en ligne)
- (en) Florian Cajori, A History of Elementary Mathematics (with hints on methods of teaching), Macmillan, (lire en ligne)
- (en) Florian Cajori, A History of Elementary Mathematics, Macmillan, (lire en ligne)
- (en) Florian Cajori, A History of Mathematics, Macmillan, (lire en ligne)
- (en) James Gow (en), A Short History of Greek Mathematics, Cambridge University Press, (lire en ligne)
- (en) John Theodore Merz (en), On the Development of Mathematical Thought During the Nineteenth Century, W. Blackwood, (lire en ligne)
- (en) Peter Barlow, A New Mathematical and Philosophical Dictionary, Londres, G. & S. Robinson, (lire en ligne)
- (en) George Abram Miller (en), Historical Introduction to Mathematical Literature, Macmillan, (lire en ligne)
- (en) Karl Fink, Wooster Woodruff Beman et David Eugene Smith, A Brief History of Mathematics, Open Court, (lire en ligne)
- (en) David Eugene Smith, History of Modern Mathematics, Wiley, , 1re éd., 69 p. (lire en ligne)
- (en) David Eugene Smith (préf. Mansfield Merriman), History of modern mathematics, Wiley, , 4e éd., 81 p. (lire en ligne)
- Autres
- (en) Bertrand Russell, The principles of mathematics, Cambridge University Press, (lire en ligne)
- (en) Alfred North Whitehead et Bertrand Russell, Principia Mathematica, — Présentation en ligne : [[ Volume 1]] et [[ Volume 2]].
- (en) Sir Isaac Newton, William Davis (rédacteur), John Machin et William Emerson (trad. Andrew Motte), The Mathematical Principles of Natural Philosophy, vol. 1, H. D. Symonds, (lire en ligne), chap. 1
- (en) Carl Friedrich Gaus, General investigations of curved surfaces of 1827 and 1825, The Princeton university library, (lire en ligne)
Articles connexes
- Articles importants
- Abus de notation, Formule logique, Notation de Landau (notation L), Notation de Dowker, Notation hongroise, Notations infixée, préfixée, polonaise et postfixée, notation polonaise inverse, Notation positionnelle, Notation additive, Système de numération
- Nombres et quantités
- Liste de nombres, Nombres irrationnels et supposément irrationnels, γ, ζ(3), √2, √3, √5, φ, ρ, δS, α, e, π, δ, Constante physique, c, ε0, h, G (Usage des lettres grecques en sciences, Table de constantes mathématiques, Table de symboles mathématiques, table des symboles littéraux en mathématiques)
- Importance générale
- Ordre des opérations, notation scientifique (notation ingénieur), Notations actuarielles internationales
- Notation pointée
- Formule chimique (formule de Lewis), Notation décimale à point
- Notation fléchée
- Notation des puissances itérées de Knuth, Théorème de Ramsey infini (théorie de Ramsey)
- Géométries
- Géométrie projective, géométrie affine, géométrie finie
- Autres
- Problèmes de Hilbert, Coïncidence mathématique, Notation aux échecs, notation musicale (Point de prolongation), codification Whyte
- People
- Mathématiciennes, mathématiciens arabo-musulmans, mathématiciens de la Grèce antique, statisticiens, statisticiennes
- Thomas Bradwardine, Thomas Harriot, Felix Hausdorff, Gaston Julia, Helge von Koch, Paul Lévy, Alexandre Liapounov, Benoît Mandelbrot, Lewis Fry Richardson, Wacław Sierpiński, Saunders Mac Lane, Paul Cohen, Gottlob Frege, George Shoobridge Carr, Robert Recorde, Bartel Leendert van der Waerden, Godfrey Harold Hardy, Edward Maitland Wright, James R. Newman, Charles Gustave Jacob Jacobi, Roger Joseph Boscovich, Eric W. Weisstein
Liens externes
- (en) « Mathematical Notation: Past and Future » (transcription d'un discours d'ouverture présenté à MathML and Math on the Web: MathML International Conference 2000) (consulté le )
- (en) Douglas Weaver, « History of Mathematical Notation » (version du 21 août 2006 sur Internet Archive)
- (en) Jeff Miller, « Earliest Uses of Various Mathematical Symbols », sur MacTutor, université de St Andrews (consulté le ).
- (en) « Finger counting », sur le site du département de chimie de Virginia Tech (version du 4 novembre 2012 sur Internet Archive)
- (en) Isaiah Lankham, Bruno Nachtergaele et Anne Schilling, « Some Common Mathematical Symbols and Abbreviations (with History) » [PDF], sur le site de l'Université de Californie (consulté le ).





































![{\displaystyle f[f(x)]}](https://img.franco.wiki/i/5f54da4ffd78a97e0493340583f3157015327436.svg)





















