Infini

Dans la religion égyptienne antique, Noun était le nom du dieu d'un océan infini existant avant la création du monde[9] - [10] - [11] - [12] - [13].

Une théorie de l'infini a été développée par le moïsme, une des « cent écoles » de philosophie nées en Chine au cours de la période des Royaumes combattants, qui remettait en cause les enseignements confucianistes et taoïstes[14] aux environs de 300 av. J.-C. Cette théorie a été publiée dans le texte fondateur de cette école, qui est un recueil des paroles et des pensées de son maître : Mozi[15].

Le Yajur-Veda documente la plus ancienne utilisation connue de nombres allant jusqu'à cent mille billions (parārdha en sanskrit[16]). Il utilise aussi le concept d'infinité numérique (pūrṇa), établissant que si on soustrait pūrṇa de pūrṇa, il reste toujours pūrṇa[17].

La Bible fait référence à l'infini en trois endroits du texte - dans le Livre de Job, chapitre 22, verset 5, dans Psaumes 147 : 5 et au livre de Nahum, chapitre 3, verset 9[18].

Les philosophes présocratiques étaient en fait les premiers physiciens (phusikoi). En effet, étant les premiers à avoir osé étudier la nature pour elle-même, ils en sont venus à instaurer une méthode d'analyse, de recherche et de réflexion qui deviendra plus tard celle des scientifiques et des philosophes. À cet effet, une grande partie du jargon scientifique encore utilisé à l'heure actuelle a été introduite par ces penseurs et avait à l'origine comme fonction d'exprimer les concepts indispensables pour faire progresser l'étude de la nature. Univers (kosmos), principe (archè)[note 1], raison (logos), nature (phusis) sont autant d'outils avancés pour pénétrer au cœur des choses et en découvrir le mécanisme ; les fonctions traditionnelles des divinités, jusqu'alors conçues comme interventions externes, sont de ce fait naturalisées. Ces penseurs avaient donc comme objectif d'internaliser les principes gérant le fonctionnement du monde, et ainsi de trouver des explications inhérentes à la nature elle-même. À travers cet objectif, ils utiliseront directement ou indirectement le concept d'infini (apeiron)[19].

Il ne reste que quelques fragments de leurs écrits, ce qui rend la recherche difficile. C'est pourquoi, afin de savoir ce que disent les présocratiques quant au concept de l'infini, il faut consulter Aristote qui fut le premier à recenser leurs thèses. Sur l'infini, c'est dans le livre III de sa Physique qu'il énumère les points communs entre les pensées de ses prédécesseurs et les raisons qui les ont poussés à croire en l'existence de l'infini.

Les présocratiques font de l’infini un principe.

Ils ne croient pas que l’infini existe en vain, non plus qu’il ait une autre valeur que celle de principe. Pour eux, tout est principe ou provient d’un principe, or, l’infini ne provient pas d’un principe du fait même qu’il en est un.

L’infini est non engendré et non corruptible en tant que principe.

L’infini est principe de toute chose, il les dirige toutes. C’est que toute chose provient d’un principe ou est elle-même principe. D’une part, l’infini en tant que principe n’a lui-même pas de principe qui l’engendre, sa limite est celle de ne pas en avoir et il est donc non engendré. D'autre part, toute génération reçoit une fin et toute corruption a un terme. Or, non engendré, l’infini ne reçoit pas de fin et il est donc incorruptible.

Immortel et impérissable, l’infini apparaît être la divinité[note 2].

Premièrement, l'infini est dans la division des grandeurs.

Les mathématiciens aussi utilisent l'infini, et ce par la division. Par exemple, la formule de l'aire du cercle π.r² est corroborée par la division du cercle en un nombre infini de triangles.

Deuxièmement, il y a infinité de la source.

En effet, la destruction et la génération ne s'épuisent pas, ce ne peut être que grâce à l’infinité de la source d’où tout est engendré.

Troisièmement, le temps est infini.

Toute génération reçoit une fin, mais la source n'a pas de principe qui l'engendre et ainsi elle n'a pas non plus de fin. Ainsi, le mouvement de la génération et de la corruption s'inscrit dans le temps et il est dû à une source inengendrée et incorruptible. C’est dire que le temps lui-même est infini.

Quatrièmement, il n'y a pas de limite en soi.

Ce qui est limité ne l'est que par autre chose, de sorte que rien ne sera limite puisque la limitation est toujours entre deux termes. L'infini est cette absence de limite en soi.

Cinquièmement, la représentation de l'infini ne l'épuise pas.

Aristote donne pour exemple les grandeurs mathématiques et ce qui est hors du ciel. Les quantités et les étendues ne peuvent pas circonscrire l'infini par représentation. Autrement dit, on ne peut pas cerner l'infini dans son ensemble, car l'infini est toujours plus grand que ce qu'on aura cerné.

Il est toutefois possible, à partir des fragments et des commentaires, de distinguer la pensée de chacun des présocratiques et de la comprendre pour elle-même.

Schémas du modèle de l'univers d'Anaximandre. À gauche, le jour en été ; à droite, la nuit en hiver.

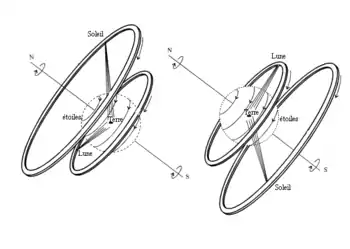
Le concept d'infini (apeiron) fut pour la première fois introduit dans la pensée du philosophe Anaximandre (vers -610 Milet – vers -546), élève de Thalès. Sous son influence, il voulut se pencher sur le fondement de l'univers, et c'est ainsi qu'il en vint à postuler l'infini comme principe et comme substrat des choses qui existent. En effet, le rôle de substrat ne peut être assigné à l'un des quatre éléments (l'eau pour Thalès, l'air pour Anaximène, le feu pour Héraclite), car ils sont changeants, dépendent les uns des autres et aucun ne peut être privilégié. Il faut donc, au-delà des éléments, une autre nature qui agit comme substrat d'où sont engendrés tous les mondes. Ce substrat, c'est l'infini, le principe qui engendre l'univers sous l'influence d'un mouvement éternel. Le mouvement éternel est en constante production, il s'agit en ce sens d’un « retour générique ». Ce retour a besoin d’un principe matériel qui doit être inépuisable afin de tout produire éternellement. C’est celui de l’apeiron et c’est en ce sens que l’infini est aussi mouvement éternel chez Anaximandre.

Parmi ses doctrines, l'école avance celle de l'éternel retour : les choses seront de nouveau les mêmes. Si pour d'autres philosophes, comme Anaximandre ou Héraclite, un retour générique peut être observé, chez certains pythagoriciens il existe un retour individuel qui peut se reproduire à l'infini. En effet, s'il y a 1) un nombre fini d'événements possibles, 2) si chaque événement possède une cause et que 3) une même cause doit toujours produire un semblable effet, il en résulte qu'au sein d'un temps infini les événements reviennent nécessairement[20]. Dans l'Éthique à Nicomaque, Aristote dit que pour les Pythagoriciens le mal relève de l'infini.

Pour Héraclite (seconde moitié du VI^e siècle av. J.-C., vers 544-541 av. J.-C Éphèse), le feu est le principe de l'univers : toute chose est convertible en feu et le feu en toute chose. D'une part, l'infini s'y retrouve à travers la génération car pour lui, toute chose advient par le conflit et la nécessité (toute chose est mue vers son contraire). Mais le feu, en tant qu'unité fondamentale de cette pluralité contradictoire, n'est jamais épuisé par ces tensions dynamiques, par ces transformations. D'autre part, l'infini caractérise le temps car pour Héraclite, l'univers n'a ni commencement ni fin. Le cosmos était, est et sera toujours feu éternel.

Quant à Parménide (fin du VI^e siècle av. J.-C. Élée - milieu du V^e siècle av. J.-C.), la conception de l'infini inhérente à sa pensée se retrouve dans l'explication de l'immobilité et de l'éternité de l'être, et ce contrairement à Héraclite. En effet, Parménide considère que l'être ne peut pas changer, sinon il ne serait pas. Ainsi, il doit être immobile. De plus, la génération et la corruption sont également des formes de changement, et c'est pourquoi l'être doit être éternel, c'est-à-dire qu'il est inengendré et impérissable. L'infini est donc nécessaire à l'existence d'un être éternellement identique.

Mélissos, élève de Parménide, considère que ce qui existe, ou plutôt ce qui est, doit être unique : il n'existe qu'une seule chose. Fondé sur les dires de son maître, il affirme qu'une chose qui existe, existe toujours, mais il ajoute qu'elle doit également toujours être infinie en grandeur. L'argument prend comme point de départ l'impossibilité du vide. Par exemple, s'il n'y a rien entre plancher et plafond, c'est dire que le plancher et le plafond sont contigus, et qu'il n'y aurait pas de séparation entre ces deux termes. Le vide ainsi expulsé, s'il y a de l'être, il n'y a que de l'être. Ensuite, toute chose doit être dans un espace et il n'y a qu'un espace, or ce dernier est occupé pleinement par l'être et par un être qui est unique. En effet, nul ne peut dire de l'être qu'il est et qu'il n'est pas, ni dire qu'un être est à certains endroits et pas à d'autres. C'est pourquoi l'être est infini en grandeur, c'est-à-dire qu'il n'y a pas de limite à l'être.

En ce qui concerne Démocrite (460 av. J.-C. Abdère - 370), la nature est constituée de petites substances illimitées en nombre qui se trouvent dans un lieu qu'il nomme l'infini. Cette infinité de petites substances qui nagent dans un vide infini et éternel parfois s'agglomèrent et forment les corps visibles à travers leur mouvement. L'infini se retrouve donc dans une division des corps en une infinité de substances, ce qui constitue la première théorie atomiste.

D'autres penseurs présocratiques ont également utilisé le concept d'infini dans leurs recherches, tels que Anaximène, Alcméon de Crotone, Xénophane et Zénon d'Élée.

Zénon d’Élée montrant à ses disciples la porte du Vrai et celle du Faux, fresque de l'Escurial, Madrid, fin du XVI^e siècle.

Zénon est un philosophe grec de l’Antiquité (environ 400 av. J.C.). Habitant d’Élée, il avait comme maître Parménide qui défendait le fait que la réalité est immuable. Zénon ne traite pas directement du sujet de l’infini. Il se sert plutôt de la notion d’infini pour montrer que la manière de décrire un problème peut conduire à l'impossibilité de traiter celui-ci. La méthode de Zénon consistait à utiliser des prémisses admises par tous et d’en déduire des conclusions absurdes ou contraires. Il montrait ainsi non que le mouvement n’est qu’une illusion, ce que nul ne pouvait soutenir, mais que le décrire sans précaution menait à des contradictions. On doit de nombreux paradoxes à Zénon (au moins une quarantaine), mais seuls quelques-uns sont connus, à travers les écrits d’Aristote. Des quatre paradoxes sur le mouvement cités par Aristote, deux utilisent l’infini pour prouver que les prémisses affirmant la possibilité du mouvement aboutissent à l’absurde.

Dans les deux paradoxes qui suivent, Zénon utilise la prémisse selon laquelle l’espace peut être divisible à l’infini pour montrer que si tel était le cas certaines façons de le décrire interdiraient de l'explorer. La portée philosophique de Zénon est incontestable ; selon Aristote, il aurait été l’inventeur de la dialectique.

Si le mouvement existe, un corps en mouvement doit se déplacer sur une certaine distance en un temps fini ; mais avant d’avoir parcouru toute la distance, le corps doit d’abord en avoir parcouru la moitié ; et avant d’en avoir parcouru la moitié, il doit avoir parcouru la moitié de cette moitié. Puisque toute distance est divisible en moitiés, et ce, à l’infini, et puisqu’il est impossible de parcourir un nombre infini de positions en un temps fini, le mouvement n’existe donc pas.

Achille, héros de la mythologie grecque, ne peut rattraper la tortue qu’il poursuit ; en effet, avant de la rattraper, il doit d’abord atteindre le point d’où celle-ci est partie au début de la course. Mais pendant ce temps, la tortue continue d’avancer d’une certaine distance ; même si cette distance est moins grande que celle parcourue par Achille (car la tortue est plus lente), elle avance quand même, elle n’est pas immobile. Ainsi, durant le temps qu’il faut à Achille pour parcourir cette deuxième distance, la tortue a encore parcouru une certaine distance. Donc, même si cette distance diminue à chaque étape, la tortue ne sera jamais rattrapée par Achille[21] - [22].

Plotin (205 - 270 ap. J.-C.) déclare : « Il ne faut pas redouter l'illimitation dans l'intelligible » (Ennéades, V.7.1). Plotin affirme l'infinité de l'Un, apeiria. Alors qu'auparavant l’infini, apeiron, représente le degré inférieur de l’existence, ou même un pur non-être, pour Plotin, l’essence de la matière reste infinie dans ce sens négatif, elle devient un attribut positif des trois hypostases (l’Un, l’Intelligence, l’Âme universelle). Ennéades II.4.15 : « Comment l'illimité peut-il donc exister là-bas [dans l'intelligible] et ici [dans la matière] ? C'est qu'il y a deux illimités. Et en quoi diffèrent-ils ? Comme un archétype et une image. L'illimité d'ici est donc moins illimité ? Il l'est davantage, car plus une image fuit l'être et le vrai, et plus elle est illimitée. En effet, l'illimitation est plus importante dans ce qui est moins défini, car le moins dans le bien est un plus dans le mal. Ainsi donc, ce qui est là-bas, parce qu'il est davantage être, est illimité seulement en tant qu'image, alors que ce qui est ici, parce qu'il est moins être, dans la mesure où il fuit l'être et le vrai, tiré qu'il est vers la nature de l'image, est véritablement illimité. »[23]

Avicenne (980 Afshéna, près de Boukhara, dans la province de Grand Khorasan - 1037), pour établir sa métaphysique, a repris celle établie par Aristote, mais lue à travers Al-Fârâbî et le néoplatonisme[24]. C’est-à-dire qu’il va comprendre des notions aristotéliciennes, mais dans un contexte théologique. Ainsi, il reprend l’idée du monde éternel, mais dans une métaphysique créationniste[25]. Dans le cadre de l’infini, il est évident que l’existence d’un Dieu viendra donner un sens nouveau à la métaphysique d’Aristote car Dieu amène des notions d’infini qui ne sont pas présentes chez Aristote. Avant de poursuivre, il faut définir certains concepts afin de montrer comment Avicenne les utilise.

La puissance est définie comme étant : « toute disposition se trouvant dans une chose et étant principe de changement »[26], tandis que l’acte (ou l’actualisation) étant ce passage de l’état de repos à l’état actif, une chose changeant d’état passerait de la puissance à l’acte. On peut prendre par exemple, la graine qui détiendrait l’arbre en puissance et qui deviendrait acte une fois celui-ci poussé. À ce sujet Aristote accepte l’infini en puissance (sous forme d’infini par division et par addition), mais rejette l’infini en acte. Avicenne va rajouter une sous-division entre actualité forte/faible et potentialité forte/faible[27].

Notons tout d’abord que Dieu est par définition infini et c’est le principe premier d’où tout émane[28], mais Dieu n’est pas le seul être infini ; il y a une dépendance ontologique des intelligences célestes (qui sont au nombre de dix) envers le premier principe, dépendance traduite par le désir de se rapprocher de la perfection de Dieu. Le désir comme principe de motion étant le fait de vouloir atteindre Dieu, lui ressembler. Ce désir de perfection, serait le principe de tout mouvement selon Avicenne[29]. Ainsi, les intelligences céleste en désirant le premier principe feraient mouvoir les sphères leurs correspondant dans un mouvement infini.

Avant de poursuivre, il faut préciser que le mouvement en question dans le monde supralunaire est différent de celui dans le monde sublunaire[30]. Dans le premier cas, le mouvement est constant ; il a toujours la même vitesse. C’est pourquoi on peut dire qu’il y a un infini présupposé pour les intelligences célestes. Cependant, dans le monde sublunaire, le mouvement est sujet à la décélération et l’accélération.

Pour conclure sur ce point, il faut nommer une autre preuve abondant dans le sens de la présence de l’infini chez les intelligences célestes, c’est-à-dire, le passage où Avicenne dit que même ce qui est infini (et nécessaire) requiert une cause[31]. Enfin, notons que si Avicenne parle de l’infini dans le monde supralunaire, il ne le classifie pas comme il va le faire pour l’infini présent dans le monde sublunaire. Probablement parce que l’infini métaphysique ne présente pas a priori autant de problèmes que l’infini dans un monde limité (physique).

Tout d’abord, l’infini en acte est amené par la théologie ; les âmes (des hommes) étant immortelles, il y en a donc une infinité dans un monde éternel[32]. C’est d'ailleurs ce qui caractérise l’infini en acte fort dans l’avicennisme.

L’infini en acte faible étant quant à lui défini par les évènements et les années passés[27]. Pour bien comprendre ce type d’infini, il faut maintenant s’attarder au concept de causalité. Car, selon Avicenne, il y aurait des causes accidentelles (ou adjuvantes) en nombre infini. En d’autres termes, il y a une succession infinie de causes préparatrices. Ici entre en jeu la distinction entre causes essentielles et causes adjuvantes. Les causes essentielles (ou vraies) étant liées au mouvement, au continu, car elles demeurent avec l’effet. Les causes vraies « empêchent la non-existence de la chose »[33]. Les causes adjuvantes sont secondaires car elles sont antérieures à la chose. Celles-ci seraient en nombre infini selon Avicenne. On peut penser à la relation père/fils qui remonterait de génération en génération pour expliciter ce fait. Car, dans le contexte d’un monde éternel, il y a une infinité de relations filiales. En effet, « […] ce qui va ad infinitum c’est un individu qui vient après un autre […] »[34].

En ce qui concerne l’infini en puissance fort, il est toujours le même que l’infini en puissance d’Aristote, à savoir l’infini par division et par addition. C’est pourquoi il ne sera pas plus détaillé dans cet article. En effet, comme dans les paradoxes de Zénon, on peut facilement imaginer la division d’une ligne en quatre parties, la division de chacune de ces parties en quatre et ainsi de suite, à l'infini.

Concernant l’infini en puissance faible, il se trouve dans le mouvement. Tel que mentionné précédemment, ce mouvement ne correspond pas à celui des sphères célestes. En effet, celui-ci, n’est pas réellement continu et peut se regarder de différentes façons. On peut déjà le voir comme le mouvement général d’un corps. Cependant, cette définition du mouvement ne sera pas celle important dans le cas de l'infini en puissance faible ; l’impulsion concrète d’un corps à un instant précis étant plutôt la définition à retenir[27]. En d'autres termes, le passage d’un temps A à B serait un mouvement constitué d’une infinité de temps. On peut penser à une addition infinie de points mis bout à bout pour former une ligne. Cette ligne, comme le mouvement, serait d’apparence continue mais serait en réalité constituée de plusieurs points intermédiaires[35].

Dans une démonstration du mouvement continu des anges au Livre II de l'Ordinatio, Scot (1266 Duns - 1308) soulève deux paradoxes qui entreront dans la postérité. Dans sa défense, il voudra réfuter la thèse selon laquelle le continu est formé d'indivisibles. Chez Aristote, dans Le Livre VI de la Physique, il est clair qu'« il est impossible qu'un continu soit formé d'indivisibles, par exemple qu'une ligne soit formée de points, s'il est vrai que la ligne est un continu et le point un indivisible »[36], mais cette preuve inspirée de l'autorité du Philosophe ne lui suffit pas. Il proposera deux problèmes géométriques du même esprit montrant tout le contradictoire d'une telle théorie.

Dans l'une des deux, on trace deux cercles concentriques à partir d'un centre a. Le petit, noté D et le plus grand, noté B. Scot dira que puisque, selon cette théorie, la circonférence du grand cercle est formée de points, il est possible d'en identifier deux, b et c. Du point a, traçons une ligne droite le joignant à chacune de ces deux points de manière que les deux droites formées coupent le petit cercle D. La question : les droites ab et ac coupent-elles D en un seul point ou en deux points distincts ? S'il s'agit du même point, l'une des deux droites ne sera plus droite (mais courbe) ce qui entre en contradiction avec la prémisse du départ. Dans le cas contraire, B et D incluraient le même nombre de points, pourtant, fait remarquer Scot, il est impossible à deux cercles inégaux d'être composés d'un nombre égal de parties égales. Il en découle qu'un continu, ici représenté par la ligne, ne peut être composé d'un nombre de points discrets[37].

Le paradoxe des cercles

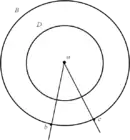
Bien que Scot lui-même n'ait pas explicité la chose dans ces termes, pour sa postérité, il s'est retrouvé à illustrer à l'aide de ces figures géométriques, en germe, certaines des découvertes les plus importantes concernant l'infini mathématique se retrouvant entre autres chez Georg Cantor. Les rayons issus du centre créant entre les points des deux cercles une correspondance biunivoque, le paradoxe soulève la possibilité pour deux ensembles infinis d'indivisibles d'être égaux malgré leurs tailles manifestement inégales[38].

D'ailleurs, dans une autre démonstration, Duns Scot se frottera à de pareils débats quant à la grandeur des infinis. Scot à la question 3 du livre II, distinction 1 de l'Ordinatio rabat l'objection selon laquelle il serait impossible pour Dieu de produire quelque chose d'autre que lui-même sans que cette production ait un commencement[39]. Selon cette objection, si la création est ab aeterno sine principio, l'infini qui a mené jusqu'à hier est équivalent à l'infini qui s'est écoulé jusqu'à aujourd'hui ce qui va à l'encontre de l'axiome d'Euclide voulant que la partie soit toujours plus petite que le tout. À cela, dans un premier temps, le Docteur répondra que ces deux dernières caractérisations ne sont applicables qu'aux grandeurs finies puisque les choses se divisent en fini et infini avant que « plus grand » ou « plus petit » ne s'appliquent. Cependant, ses adversaires soulèvent le problème qu'une création de toute éternité produirait une quantité infinie d'âmes en acte, or, une telle chose est impossible selon le Philosophe. Devant cette objection, Scot développe davantage : « Tout ce qui ne peut pas être fait par Dieu en un jour, parce que « cela implique contradiction » ne pourrait, pour la même raison, être fait par lui au cours d’un temps d’une durée infinie. »[40] Il en vient à cette conclusion : « Il apparaît donc, que les instants de ce jour – voire de cette heure – ont une infinité égale à celle des instants infinis de ces jours infinis. »[40] Cette intuition se verra, entre autres, confirmée par Richard Dedekind dans sa définition d’un ensemble infini qui se caractérise justement par l'équivalence entre le dit ensemble infini et une de ses parties propres de ce point de vue[41].

Il n’en demeure pas moins que le fondement de l’affirmation par Scot qu’il existe quelque chose comme un infini en acte est théologique. Jean Duns Scot refuse qu’il soit impossible pour Dieu de créer spontanément une infinité en acte. En effet, selon Aristote une grandeur ne peut être infinie qu’en puissance. Or, voulant construire l'idée d'une nature infinie intensivement (selon la qualité), Scot fait un passage obligé par la démonstration d'une grandeur extensivement (selon la quantité) infinie en acte[42]. Selon la définition d’Aristote au Livre III de la Physique, l’ « infini est ce qui est tel que lorsqu’on en prend une quantité, c’est-à-dire quelque grande que soit la quantité qu’on prend, il reste toujours quelque chose à prendre »[43], donc un tout infini n’est qu’une réalité potentielle et par cela, conclut Scot, imparfaite. Pour remédier à une telle situation, le médiéval imagina à partir de cet infini potentiel ce qu’il serait en acte :

Pour notre propos, dit Duns Scot, transformons la notion d’infini potentiel dans la quantité en la notion de l’infini en acte dans la quantité en supposant qu’il puisse être en acte dans la quantité. Nécessairement, la quantité croîtrait toujours, en prenant une partie après l’autre, mais si nous imaginons que toutes les parties qui peuvent être prises successivement le sont simultanément, alors nous aurons une quantité infinie en acte, puisqu’elle sera aussi grande en acte qu’elle l’est en puissance. Si donc toutes les parties étaient conçues comme présentes en acte simultanément, l’infini ainsi imaginé serait véritablement un tout et serait véritablement parfait, car il n’y aurait rien au dehors. Bien plus, nulle quantité ne pourrait lui être ajoutée, car alors il pourrait être excédé. »[44]

Par ce passage, Jean Duns Scot fait de l’infini non pas ce qui laisse toujours quelque chose derrière, mais bien ce qui excède le fini selon toute proportion déterminée ou déterminable[45].

Le passage de l'infini en quantité à l'infini sous le mode de la qualité ne se fait pas non plus sans Aristote. Bien que chez ce dernier l'infini ne s'applique qu'aux grandeurs, il ouvre une porte au livre V de sa Métaphysique admettant la transposition de notions quantitatives à d'autres objets « par extension »[46]. À la question 6 du Quodlibet, Scot commente ce dernier passage et montre que des termes quantitatifs comme petit, grand, moins, plus, sont applicables à tous les êtres, peu importe leur genre. La transposition de la physique à la métaphysique est, par là, possible. Toutefois, Scot voudra faire de l'infini non un accident mais une quantité d'être ou quantité de perfection. Il tire de l’océan d'être infini de l'essence divine de Jean de Damas le concept de l'infinité comme mode d'être intrinsèque d'une nature infinie: « de même que l'océan ne serait l'océan sans l'immensité de sa masse, de même l'essence divine ne serait pas l'essence qu'elle est sans la magnitude qui est la sienne. »[47] Dans la mesure où nous concevons un être infini actuel en entité, explique Scot, il se doit d'être pensé sous le mode d'une quantité infinie actuelle, c'est-à-dire qu'aucun autre ne saura le dépasser en entité. En cela, il « sera véritablement un tout, et un tout parfait »[48].

Dans la métaphysique de Jean Duns Scot, le concept d'infini est assimilé aux transcendantaux. Les transcendantaux, outre l'étant, sont des attributs qui peuvent être, chez le Docteur Subtil soit : des attributs disjonctifs (infini/fini, possible/nécessaire, en acte/en puissance, etc.) ; des attributs convertibles (l'un, le vrai, le bien…) qui sont directement coextensifs avec l'étant ; des perfectiones simpliciter (i.e. un prédicat qui n'admet pas de limite telle que l'intelligence divine par exemple)[49].

Le couple d'attributs disjonctifs infini/fini permet d'établir une mesure de l'être, non plus au sens strictement quantitatif, mais plutôt au sens d'un degré d'excellence de l'être. Il s'agit d'une différence strictement modale – plutôt que formelle – entre les êtres : Dieu est sur le mode de l'infini, alors que l'homme est sur le mode de la finitude. Cette précision – qui ne s'inscrit pas seulement dans la métaphysique scotienne, mais aussi dans le cadre d'un argument théologique portant sur l'existence de Dieu infère que la différence entre un être fini et un être infini n'est pas une différence générique ce qui, au sein du raisonnement du Docteur Subtil, permet de sauvegarder la simplicité divine[50].

En vertu de la théologie naturelle scotienne et, plus largement, de sa théorie cognitive, il est possible pour l’homme de connaître à l’aune de son expérience sensible. Ainsi, si la connaissance essentielle de Dieu n'est pas accessible ici-bas faute de pouvoir faire l'expérience de ce dernier, il est cependant possible de prédiquer à Dieu des attributs partagés avec lui (comme l'intelligence) en vertu de la théorie scotienne de la prédication univoque[51]. Par exemple, s'il est possible de prédiquer l'intelligence à Marie, de même peut-on attribuer l'intelligence à Dieu, mais pas sous le même mode que celui de la créature finie. Pour Dieu, il s'agira d'une perfectiones simpliciter. Il s'agit du même concept d'intelligence, mais qui n'est pas donné sous le même mode chez la créature finie et chez Dieu, être infini.

De plus, la créature finie sera aussi en mesure de parvenir à la caractérisation la plus parfaite et la plus simple du Premier principe. Comme vu plus haut, on parvient précisément à cette caractérisation positive avec le concept d'infini, sous-tendant tous les attributs que l'on peut prédiquer à Dieu[52]. Scot renverse ici l'infini en tant que concept négatif pour en faire un concept positif. En effet, on pourrait défendre la négativité du concept d'infini sur le plan étymologique par la présence du préfixe in qui implique une négation. Considéré comme tel, il serait alors contradictoire de parler de l'infini comme une caractérisation positive de Dieu. On peut analyser un tel renversement d'un point de vue logique en affirmant que, la finitude étant en soi concept impliquant une limite négative, l'ajout du préfixe in, la double négation fait naître (sur le plan logique et formel du moins) un concept positif. Cependant, pour Scot, la nature de la distinction du couple fini/infini est métaphysique et non formelle ou linguistique[53]. Ainsi, défendre la positivité ou la négativité du concept à partir de la sphère de la logique ou, plus simplement, de l'étymologie est inutile dans l'optique scotienne ; il faut plutôt admettre sa positivité comme un présupposé métaphysique.

Bradwardine (c. 1300 – 1349) a proposé l'idée d'un espace infini autour de la terre (en dehors du " firmament"), en réponse à l'impératif de l'église catholique de 1277 (en), afin de résoudre les conflits de pensée et de doctrine chrétiennes résultant de la compréhension de la philosophie et de la théologie aristotéliciennes[54], par la synthèse de géométrie euclidienne dans la compréhension chrétienne[55]. C'est ce qu'il a fait spécifiquement pour réconcilier Aristote conceptualisant l'infini avec la notion chrétienne d'un «infini de Dieu» en possession d'un pouvoir infini[56].

Oresme (c.1320 Allemagnes (ancien nom de Fleury-sur-Orne)- 1382) [57] a commencé à penser à l'infini, en partie après l'écriture de Aristote [58] et son travail Physique. Dans Questions sur la géométrie d'Eclide, Oresme a démontré la possibilité du concept de "série infini", dans sa considération, dans la continuité (et la transcendance), de l'idée de division infinie proposée par Aristote (" en division en parties, la division est elle-même divisible " [58])[59].

Galilée (1564 Pise - 1642) remarque qu'il y a une correspondance biunivoque entre les nombres et leurs carrés, d'où il déduit que l'assertion commune « le tout est plus grand que la partie » ne se vérifie pas lorsqu'on parle de quantités infinies[60]. Cependant, loin d'y trouver une motivation pour l'étude des ensembles infinis, il y voit la preuve du caractère non opérationnel de tels ensembles, position approuvée plus de deux siècles plus tard par Cauchy[61]. Ainsi donc, jusqu'à une période assez avancée dans l'époque moderne, les mathématiciens s'interdisaient d'utiliser directement les ensembles infinis et préféraient raisonner « en compréhension » sur les propriétés de leurs éléments. Ils se contentaient alors de la possibilité d'augmenter toute grandeur donnée, ou de la diminuer s'il s'agit d'une grandeur continue[61].

Dans la pensée métaphysique de Descartes (1596 La Haye-en-Touraine - 1650), seul Dieu peut être qualifié d’infini. La Méditation III offre une définition de ce dernier : « Par le nom de Dieu j’entends une substance infinie, éternelle, immuable, indépendante, toute connaissante, toute puissante, et par laquelle moi-même, et toutes les autres choses qui sont ont été créées et produites. »[64] La notion d’infini réel ou en acte est strictement réservée à Dieu ; seul Dieu est infini car il est l’être infini lui-même. Il est donc question chez Descartes d’un infini d’ordre qualitatif ; d’une perfection infinie qui existe uniquement chez l’être parfait, chez Dieu - « il n’y a rien que je nomme proprement infini, sinon ce en quoi de toutes parts je ne rencontre point de limites, auquel sens Dieu seul est infini. »[65]

La notion d’infini a toutefois aussi une place dans l’homme, dans sa pensée. Elle s’y trouve contenue en lui en tant qu’idée qui lui est innée ; l’homme possède une idée de l’infini, il est capable de concevoir, à sa manière limitée, l’infini. C’est précisément cette idée de l’infini que Descartes assimile à l’idée de Dieu en l'homme ; « la notion de l’infini […] c’est-à-dire de Dieu. »[64] Il s’agit simplement de la conception que l'on est capable de se faire d’un être infini et parfait, en d’autres termes de notre idée de la divinité. Bien qu’il ne s’agisse pas de l’infini véritable, qui lui ne se trouve qu’en Dieu lui-même, l’idée de l’infini (ou de Dieu) que l’on retrouve dans la pensée de l’homme occupe une place importante dans la métaphysique cartésienne car elle est ce à partir de quoi Descartes infère l’existence effective et réelle de Dieu (hors du cogito). C’est la preuve de l’existence de Dieu dite « par l’infini », que l’on retrouve dans la Méditation III.

L’idée de l’infini témoigne de la finitude de l’ego cartésien, du je qui pense cet infini. Le degré de perfection du contenu que représente cette idée est d’une telle ampleur qu’il rend manifeste la finitude du je dans lequel loge cette idée même. Ultimement, Descartes veut montrer qu’il est impossible que cette idée, dont le contenu possède un tel degré de perfection, puisse être la création du je qui pense, puisse être causée par lui de quelconque manière[66]. Cela étant, elle ne peut être « imprimée »[67] ou se trouver dans ce même je qu’en vertu d’un être qui lui soit externe, c’est-à-dire autre que le je, et qui possède formellement ou en acte suffisamment de perfection afin de pouvoir être l’auteur ou la cause du contenu de notre idée de l’infini. Pour Descartes, il ne peut s’agir que de Dieu, d'un être possédant réellement en lui l'infinité et la perfection que l’ego ne peut qu’à peine et de manière bien limitée concevoir. Descartes dira, de manière métaphorique, que l’« on ne doit pas trouver étrange que Dieu, en me créant, ait mis en moi cette idée pour être comme la marque de l’ouvrier empreinte sur son ouvrage. »[68]

Bien que l’homme soit donc capable de penser l’infini, il ne peut le faire qu’avec ses capacités limitées, celles de l’être fini qu’il est. Bien qu’il tende à le comprendre, et s’aime à le contempler, il ne pourra jamais saisir cet infini dans sa totalité, dans sa perfection. De son idée de l’infini qu’il trouve en lui, l’homme doit donc se contenter de la simple certitude qu’elle lui permet d’acquérir de l’existence effective, extérieure à sa pensée, de cet infini et que ce dernier soit non seulement la cause de cette idée mais aussi bien de l’existence de l’homme ainsi que de toute chose qui est[67]. « Et toute la force de l’argument dont j’ai usé ici consiste en ce que je reconnais qu’il ne serait pas possible que ma nature fût telle qu’elle est, c’est-à-dire que j’eusse en moi l’idée d’un Dieu, si Dieu n’existait véritablement ; ce même Dieu, dis-je, duquel l’idée est en moi, c’est-à-dire qui possède toutes ces hautes perfections, dont notre esprit peut bien avoir quelque idée sans pourtant les comprendre toutes, qui n’est sujet à aucun défaut, et qui n’a rien de toutes les choses qui manquent quelque perfection. »[67]

L’infini dans l’homme, sous forme d’idée innée, permet donc de connaître que cet infini existe actuellement hors de l’homme mais ne peut néanmoins propulser l’homme vers une connaissance absolue de cet infini. Ce serait là une contradiction avec la notion même de ce que signifie l’infini chez Descartes. En effet, l’infini ne pourrait, par sa nature, jamais être compris par le fini. Descartes dira qu’« il est de la nature de l’infini, que ma nature, qui est finie et bornée, ne le puisse comprendre. »[68] Le créateur ne saura jamais être compris par sa créature.

Notre conception de l’infini nous permet donc non seulement de constater notre propre finitude, mais également d’inférer avec certitude qu’un tel être infini doit nécessairement exister hors de nous-mêmes, bien qu’on ne puisse jamais espérer le comprendre entièrement. Descartes nomme cet être Dieu[69].

Alors que l'infini se dit de Dieu, l'indéfini se dit du monde physique et des mathématiques. L'indéfini désigne ce dont on ne peut prouver les bornes. Sa véritable nature est l'indétermination, puisque ni fini, ni infini. Tout ce qui est ontologiquement second à Dieu est seulement indéfini, c'est-à-dire qu'il traduit l'ignorance du sujet. Pourtant, Dieu lui-même échappe à l'homme. L'essence de l'infini déborde toute tentative dicible. Il y a inadéquation entre l'idée de l'infini en moi et l'infini, puisque vouloir dire l'infini, l'écrire ou le définir excède toujours la compréhension qu'on peut en avoir. L'idée de l'infini, se présente comme un paradoxe: c'est à la fois l'idée la plus claire et distincte, et l'idée la plus incompréhensible. En affirmant qu'il est faux de concevoir l'infini en niant le fini, Descartes suggère que l'on doit se contenter de se servir d'expressions négatives tout en les refusant sur le plan du sens, non seulement parce que l'essence de l'infini déborde toute tentative de le renfermer dans le langage, mais aussi que la mesure dans la positivité est essentielle à l'infini[70].

La tradition a plutôt interprété l'indéfini cartésien comme un infini en extension ou infini spatial. Ce qui est présupposé dans cette interprétation est que Descartes reprend le couple infini en acte et infini potentiel d'Aristote. Jean-Baptiste Jeangène Vilmer[70] suggère de mettre en cause cette interprétation et considérer plutôt une interprétation littérale de la notion d'indéfini dans la pensée de Descartes ; c'est-à-dire indéfini comme in-défini ou non défini. Notons qu'il y a des raisons métaphysiques pour refuser de considérer que l'indéfini soit un infini en son genre, dont le genre serait l'étendue. Ontologiquement, l'infinie positivité de Dieu implique nécessairement l'existence d'un seul infini. Aussi, l'étendue étant la marque du corps, cela constitue un défaut. On ne peut donc pas la prédiquer à Dieu, qui est infinie perfection. Enfin, puisque l'infini de Descartes n'est pas un infini de quantité, mais un infini de qualité - la perfection - on doit voir une différence de nature et non de degré entre infini et indéfini.

Cette distinction entre infini et indéfini s'explique aussi par le rapport de subordination qu'il y a entre métaphysique et physique chez Descartes. La métaphysique est la science des sciences, celle qui permet d'atteindre les principes de base et d'expliquer les fondements du savoir. Plus encore, les évidences des sciences ont besoin d'être ultimement garanties par l'existence de Dieu. La preuve de Dieu étant le fondement de l'ontologie, pour Descartes « un athée ne peut être géomètre », elle assure la validité des vérités éternelles[71].

On a noté que l'idée de l'infini se présente comme un paradoxe. La clarté de la notion d'infini, vient de l'idée innée d'infini. Dieu ayant fait l'homme à son image, il y a forcément un rapport de ressemblance entre les deux. C'est la volonté qui a pour Descartes un rôle d'image ou de marque divine. On ne peut concevoir cette ressemblance que par la même faculté par laquelle on se conçoit soi-même. Cette faculté est la volonté, soit le pouvoir d'affirmer ou de nier sans qu'une force extérieure nous y contraigne, c'est-à-dire porter un jugement qui lie des idées entre elles. On ne parle jamais de son caractère infini, mais seulement de son infinitude parce qu'elle est précisée seulement semblable[72].

Cette infinitude est le but, l'aspiration naturelle ou le désir que l'homme a pour l'infini. Pour éviter que l'infini soit objet et donc vienne contredire l'idée d'infini, il est nécessaire que l'infini soit l'origine et le but de l'homme. Ainsi, l'infini est origine puisque l'homme est marqué par lui en ayant l'idée innée de l'infini. Et l'infini est aspiration naturelle, puisque c'est la manifestation du refus du fini. L'idée de l'infini qui est en moi, c'est-à-dire en tant qu'idée innée, est le point de départ pour dépasser le solipsisme et de démontrer l'existence de l'infini. On doit ensuite remarquer que dans la conception de la volonté de Descartes, volonté et liberté sont liées, voire confondues. Il définit la liberté comme l'amplitude de notre volonté. Alors, poser que la volonté est infinie c'est dire que son amplitude est infinie, et ainsi l'homme a une infinie liberté. Si on peut affirmer son infinitude, c'est parce que la volonté porte les signes de l'infini: soit la positivité et l'incompréhensibilité. La positivité de la volonté se traduit par l'évidence du libre arbitre, alors que son incompréhensibilité réside dans le paradoxe de la finitude de mon entendement et de l'infinie volonté[72].

On peut aussi voir la cause de l'erreur dans l'infinitude de la volonté ; l'erreur est une imperfection dont Dieu ne peut être responsable, étant infiniment bon et parfait. La cause se situe donc nécessairement au niveau de l'esprit humain, dans l'usage de ses facultés. On définit l'esprit humain comme cette chose qui pense, composée de l'entendement et de la volonté. D'abord, l'entendement est une faculté passive qui reçoit les idées. Bien que l'entendement humain soit fini, il ne peut être la cause de l'erreur puisqu'une idée ne peut pas être plus ou moins vraie, seulement plus ou moins claire et distincte. Ensuite, la faculté de la volonté est active. Elle lie les idées ensemble pour former des jugements. Les relations ne peuvent pas être erronées en soi. Elle ne peut donc pas être seule cause de l'erreur. Descartes montre que l'erreur se produit lorsque la volonté dépasse les limites de l'entendement et pose des relations entre des idées qui ne sont pas claires et distinctes. Tel est l'effet de l'infinitude de la volonté[73].

En 1635 [74] Cavalieri (1598 Milan - 1647) propose une nouvelle idée de la géométrie dans laquelle les corps sont composés de surfaces infinies et les surfaces de corps de lignes infinies[75]. Il appelle son idée de l'infiniment petit en géométrie les indivisibles[76]. La méthode des indivisibles est publiée dans Geometria indivisilibus continuorum nova quadam ratione promota (1635). Cavalieri conçoit cette idée pour la première fois en 1629[77] - [78].

Pascal [79] (1623 Clermont (aujourd'hui Clermont-Ferrand) - 1662) connaissait l'infini comme un fait de réalité existant dans toutes les sciences, ce qu'il pensait être vrai en raison du fait que la nature était en réalité « un double infini »[80]. En considérant comment il est impossible de comprendre l'infini par la contemplation pour des individus, Pascal a montré comment cette impossibilité poussait grandement les individus à la recherche de la vérité dans la nature dans le cadre d'une enquête scientifique, mais il n'y a pas de capacité chez l'humain de connaître l'infini, et donc pas de capacité infinie (comme il en existe dans la nature) chez l'humain, cette seconde capacité d'infini étant nécessaire pour une connaissance correcte de la nature (synonyme de recherche scientifique)[81].

Locke (août 1632 Wrington (Somerset) - October 1704) [82] a considéré que dans les considérations sur le sujet de l'éternité, qu'il a classé comme un infini, les humains sont susceptibles de faire des erreurs[83]. Dans Essai sur l'entendement humain, il a observé comment discussions sur le sujet de l'infini semblent possibles pour les individus, du fait de la possibilité d'utiliser des mots pour exprimer des quantités d'espace, de durée ou de divisibilité, mais l'idée d'infini est en fait incompréhensible (partie 21). Locke croyait que l'infini était un attribut de Dieu du christianisme (partie 1), mais ne pouvait comprendre la nature d'un être sans commencement, et ne pouvait donc pas compléter sa propre idée d'un "être éternel" (partie 17). Il pensa que comprendre l'infiniment petit était plus facile que l'infiniment grand (partie 18)[84].

C’est avec Gottfried Wilhelm Leibniz (1646 Leipzig - 1716) que l’actualité de l’infini sera pour la première fois objet d’une véritable analyse, étant donné que cette actualité est affirmée positivement. L’infini joue dans le système leibnizien un rôle fondamental quant à l’existence de toute chose. Cette affirmation s’oppose directement à la pensée aristotélicienne selon laquelle le concept d’infini ne peut être pensé que comme un possible. Selon Leibniz, l’infini en acte est la condition de possibilité de toute opération d’addition et de division, en tant que sa réalité est toujours déjà présupposée[85].

Selon Leibniz, seul Dieu et ses attributs peuvent véritablement être dits « infinis ». En ce sens, tous les autres contextes où l'on trouve l’infini ne sont que des expressions plus ou moins parfaites de l’infinité de Dieu. Cette absolue infinité s’explique par la prémisse selon laquelle Dieu est parfait, la perfection étant ici entendue comme « la grandeur de la réalité positive prise précisément, en mettant à part les limites et bornes dans les choses qui en ont ». Dieu ne pouvant être limité, c’est sa perfection même qui est infinie. De par son infinité, Dieu est d’ailleurs le terme ultime de la série infinie des faits contingents du monde, en tant que raison suffisante dernière[87].

C’est dans les idées de Dieu que l’on trouve une infinité de mondes possibles. L’infini y est donc d’abord possible, puis réel. Le passage du possible au réel est régi par le principe de la détermination du meilleur. En effet, la création du meilleur monde possible par Dieu s’effectue selon un calcul qui prend en considération l’infinité des possibles. Par la combinatoire, Dieu compare d’abord l’infinité des possibles, puis également l’infinité des systèmes possibles, pour finalement déterminer le système présentant le plus haut degré de perfection. Il y a donc dans les idées de Dieu infinité d’infinis[88].

L’infini se trouve également dans les réalités individuelles (monades). Les monades étant par nature perceptives et appétitives, elles rassemblent une multitude de perceptions dans leur unité substantielle. Leur capacité de représentation n’est donc pas limitée à un aspect partiel des choses, mais à la multitude des choses dans l'univers, ce qui pousse Leibniz à affirmer « qu’elles vont toutes confusément à l’infini, au tout » (Monadologie par.60) . Il ne faut cependant pas se méprendre quant à la nature bel et bien finie de la monade. Ce type de réalité est fermée, « sans porte ni fenêtre », mais elle accède par ces états à la multitude des choses de l’univers. La monade est ainsi une réalité finie dont la capacité représentative est infinie. La différence entre l’infinité de Dieu et l’infinité de la monade est dès lors une différence quant à la manière d’être infini.

L’univers accède également à l’infini, mais en un tout autre sens. L’univers n’est ni une totalité, ni une réalité unique et simple. Il est plutôt un « amas d’un nombre infini de substances ». C’est donc que le monde créé, de par l’infinité des substances et la division infinie de la matière, ne peut être unifié. Il est donc ici question d’un agrégat d’une infinité de réalités à quoi l’on ne peut assigner de limite[89].

La nature est pour Leibniz une structure de corps étendus, ces corps étant divisibles à l’infini. Leibniz compare d’ailleurs la nature à un étang habité par une multitude de créatures, où chaque parcelle de l’étang contient en lui-même une infinité d’étangs. C’est donc que la division de la matière est à comprendre non seulement comme une première division à l’infini, mais également selon une multitude de divisions où chaque partie actuellement divisée est elle-même divisée à l’infini, et ainsi à l’infini. Cette division est d'ailleurs imaginée par Leibniz selon qu'il s'agirait de « plis» qui vont à l'infini. La divisibilité des corps à l'infini doit être représentée non pas comme un nombre infini de grains de sable, mais comme les plis infinis d'une feuille de papier, où l'on ne peut atteindre le pli ultime[90].

Conceptuellement, la présence de la notion d’infini dans le calcul infinitésimal est problématique. L’utilisation des expressions « dx » et « dy », qui semble faire référence à une quantité infiniment petite de temps ou d’espace peut en effet être la source de confusion. Leibniz mentionne à cet égard que le calcul infinitésimal est autonome opératoirement quant à sa métaphysique, et que l’écriture infinitésimale possède une valeur strictement instrumentale. Le calcul infinitésimal peut donc être dit indépendant de la métaphysique leibnizienne du point de vue de son fonctionnement. L’infini mathématique, en tant qu’infini quantitatif, s'apparente davantage à un « faux infini », ou à un infini simplement possible ; les différentielles sont des grandeurs qui n’existent pas avant d’être instrumentalement posées[91].

L’infini actuel et l’infini possible peuvent tous deux être objets d’une science. En ce qui a trait à l’infini mathématique, bien qu’il soit considéré comme un « faux infini » (potentialité), il est clair pour Leibniz qu’il est possible de connaître la loi d’une progression interminable de quantité. En ce sens, la raison suffisante de cette progression est accessible ; nous en avons donc une connaissance.

Le concept d’infini en acte est une idée innée. En ce sens, l’idée d’infini est évidente par elle-même et donc soumise uniquement au principe de non-contradiction, ce qui la rend rationnelle. Il est également possible d’avoir une idée adéquate de l’infini métaphysique ou véritable, c'est-à-dire qu'il est possible d'en avoir une connaissance ou d'en présenter une définition dont l'on connait distinctement tous les termes. Dieu, de par ses attributs infinis, soit l'éternité et l'immensité, peut alors être connu. Or les monades sont des réalités finies qui ne peuvent percevoir l’infini que du point de vue dans lequel elles sont placées. C’est donc seulement en Dieu que la compréhension parfaite de l’infini est possible[92].

La première des quatre antinomies de Kant (1724 - 1804) est exprimée comme suit dans la Critique de la raison pure[93] :

« Le monde a un commencement dans le temps […], relativement dans l’espace, contenu dans certaines limites. » : II serait, en effet, absurde d’admettre une série à la fois infinie et réalisée. La totalité des êtres ou des phénomènes forme un nombre qui dépasse notre imagination, mais qui est un nombre réel, et l’infini dépasse tous les nombres. Le passé contient un nombre d’êtres et de phénomènes auquel chaque instant ajoute. Il est contradictoire de nommer infini ce qui augmente ou peut augmenter. Le même raisonnement réfute l’éternité du passé : l’éternité est infinie, inaugmentable et chaque instant augmente le passé.

« Le monde n’a ni commencement ni limites spatiales mais il est infini […] à l’espace que par rapport au temps. » : Si le monde n’était éternel et sans mesure, il s’envelopperait donc d’un temps et d’un espace vides. Mais un temps vide ne renferme aucune cause, aucune condition, aucune possibilité de commencement, et rien n’aurait jamais pu commencer. Borner le monde dans le temps, c’est l’annihiler. Et un espace vide n’est rien. Dire qu’un espace vide limite le monde, dire que le monde est limité par rien, c’est dire tout ensemble que le monde est limité et qu’il n’est pas limité.

Le projet du système hégélien de la dialectique et de l’infini a pour ambition de dépasser les oppositions philosophiques de l’infinité de la substance objective chez Spinoza et de la finitude de l’entendement humain chez Kant. C’est à partir de la première antinomie cosmologique du fini et de l’infini dans la Critique de la raison pure que Hegel (1770 - 1831) forme sa conception du véritable infini. Pour Kant, tâchons de rappeler que l’absolu n’est jamais donné dans l’intuition, mais il est forgé de toutes pièces par l’esprit en tant que simple concept, comme idée transcendantale. Cette idée de l’infini joue le rôle de pure fiction pour l’homme, fiction utile comme le déclarait Leibniz, alors qu’elle devient une idée-limite, une projection trans-empirique, peut-être nécessaire comme outil de développement de la connaissance, mais n’ayant vraisemblablement aucune réalité ontologique[94]. Selon Hegel, l’erreur de Kant aura été de ne concevoir qu’un infini quantitatif, puisque le concept d’éternité, comme progrès temporel interminable ne prend forme qu’en concevant une droite interminable ou encore une suite infinie de nombres naturels. Il en va de même pour l’infini spatial qui présuppose nécessairement une grandeur inexhaustible dans laquelle la finitude viendrait s’engouffrer ; encore une fois, l’argument est circulaire[94]. Les catégories a priori de la sensibilité que sont le temps et l’espace chez Kant constituent la solution transcendantale au problème de la première antinomie, mais elles ne peuvent rendre compte pour Hegel de la dialectique interne de l’esprit seule apte à subsumer les antagonismes qu’il porte en son sein même[94]. Si l’infini hégélien est dit qualitatif, c’est bien parce qu’il ne se résume pas dans l’énumération ou l’itération de séries de nombres ou dans la somme de ces séries, mais bien parce qu’il réside dans le rapport qu’elles entretiennent ensemble.

Les mathématiques ont pour Hegel, un caractère essentiellement analytique ; non seulement la valeur de vérité des équations mathématiques ne tient pas de l’expérience sensible, mais elle dérive toujours en quelque sorte de sa conformité avec un paradigme au sein duquel sont présupposées des lois et des définitions a priori (au sens kantien). En ce sens, pour Hegel, le procédé analytique représente, contrairement à Kant, « la pure immanence des déterminations à la totalité originelle présente sous la modalité de l’en-soi »[95]. Autrement dit, ce n’est pas le nombre comme objet qui déploie de son essence les lois et mécanismes qui caractérisent son intériorité pure, mais elles sont insérées de l’extérieur par l’esprit et deviennent de sorte le miroir du fonctionnement de l’esprit humain et de son organisation intérieure. Ultimement, « l’objet, le nombre, n’est que la pensée, et la pensée abstraite de l’extériorité elle-même […] En raison de cette extériorité pure et de cette absence de détermination propre, le penser a dans le nombre une matière déterminable infinie qui n’oppose aucune résistance. »[95]. La vérité pour Hegel, ou plutôt, le déploiement de la connaissance est toujours à la fois un procédé objectif et subjectif, une méthode à la fois analytique et synthétique. La connaissance mathématique partage donc ce caractère analytique avec la connaissance conceptuelle, toutefois, elle se différencie de cette dernière en n’étant qu’analytique, alors que la connaissance du concept est également un procédé synthétique. Pour Hegel, le véritable infini est dans la relation qualitative qui s’établit dans le rapport entre deux grandeurs quantitatives. Comme Leibniz l’avait remarqué avant lui, ce ne sont pas les quantités infiniment petites ou infiniment grandes qui sont importantes, mais leur différence qui est infinitésimale[94]. Le passage de la quantité en qualité s’effectue à travers une relation dynamique engendrée par la raison qui résulte en une mesure, une proportion, ce qui pour Hegel signifie l’assimilation mutuelle du déterminant (qualité) et du déterminé (quantité).

La conception de l’infini élaborée chez Hegel n’avait pas de prime abord des prétentions mathématiques ou pratiques, mais essentiellement métaphysiques et c'est bien en ce sens que sa vision de l’infini devenait celle de la dynamique du concept absolu. Ainsi il faut également prendre en considérations que pour Hegel - axiome fondamental de tout son système qu’il emprunte à Spinoza -, toute détermination est du même coup une négation et par conséquent, la négation de la négation reflète l’automouvement du concept absolu. En résulte que la finitude et l’infini ne sont pas liés de manière externe par opposition l’une à l’autre, mais entretiennent plutôt une relation dynamique internalisée, l’infini absorbe en lui la finitude comme un des moments de son perpétuel déploiement. « Pour Hegel, ce devenir processuel est un infini dynamique ou qualitatif, et sa figure est celle du cercle sans point initial et sans point final – et non pas l’image de la droite infinie ou de la suite illimitée des nombres naturels. »[94]. Selon Hegel, l’histoire de l’être est un devenir perpétuel, « toute forme donnée est poussée à se dépasser, selon la nécessité d’une poussée, d’une pulsion, immanente, constitutive de la nécessité de sa transcendance. »[96]. Le mécanisme inhérent à ce mouvement universel est la dialectique, « la loi de la pensée et du réel qui, progressant par négations successives, résout les contradictions en accédant à des synthèses elles-mêmes toujours partielles et appelées à être dépassées »[97]. Une conception particulière est toujours en elle-même un système positif et cohérent et en ce sens, il contient en lui un fragment du concept absolu qu'il représente de manière incomplète. Une idée dépassée ne disparaît jamais totalement, elle est plutôt submergée dans un nouveau système au sein duquel le fragment de son absolutisme est ratifié et incorporé. La négativité qui est au cœur de la dialectique s’effectue toujours dans un rapport dont elle est le principe médiateur. En d’autres mots, c’est le négatif qui effectue le rapport structurel entre une intériorité idéelle et une extériorité manifeste. En ce sens, le négatif s’apparente à l’essence de la chose, la poussée directrice, le moteur ontologique de l’être. Ce travail du négatif, inscrit au cœur même du devenir, anime pour Hegel toute histoire particulière[97]. Ce mouvement est pour Hegel un infini abstrait, un mécanisme universel à l’œuvre en toutes choses positives.

Finalement, ce qui est fini, par définition toujours en transition, est toujours en devenir, toujours appelé à être transcendé, dépassé vers l’infini. L’absolu contient donc en lui tous les moments de la finitude, l’absolu s’aliène lui-même à partir de lui-même pour finalement s’extérioriser comme esprit. L’infini chez Hegel est donc esprit absolu, idée absolue ou concept absolu, synonymes de la totalité du système de la philosophie. Si l’esprit ou l’idée est dite infinie chez Hegel, c’est que l’infinité est l’être de ce qui est sursumé et n’est que sursumé[98].

Georg Cantor en 1894

Georg Cantor (1845 Saint-Pétersbourg - 1918) – mathématicien de formation – constate, au fil de ses travaux, que l’analyse mathématique est insuffisante à saisir complètement l’essence de l’infini[99]. En fait, il se penche sur la question à travers les ensembles, dont les propriétés n’avaient pas été clairement élucidées avant lui. Celles-ci semblaient triviales pour les ensembles finis, alors que celles des ensembles infinis concernaient plutôt la philosophie. Cantor devient donc le fondateur de la théorie des ensembles, une méthode « plus rapprochée de la philosophie générale »[99] et dont le développement constituera un « achèvement aux conséquences majeures dans l’histoire des mathématiques »[100]. La théorie des ensembles, plus précisément la théorie des nombres transfinis, qui en constitue le noyau[99], servira d’assise à une réflexion sur un éventail d’infinis différents. Cantor distinguera donc trois notions différentes d’infini : l’infiniment grand, qu’il analyse et hiérarchise et pour lequel il est reconnu (sections 1 à 4) ; les infinitésimaux, qu’il nie et rejette (section 5) ; enfin, l’infini absolu, sur lequel il fonde sa métaphysique de l’infini[101] (section 6).

Ainsi, l’appareil conceptuel déployé par Cantor se fonde sur des distinctions mathématiques complètement nouvelles, qui font de l’infiniment grand un objet à part, néanmoins analysable, mais qui contredit l’intuition[102]. Cantor croit que l’arithmétisation de l’infini est possible, autrement dit, il pense que l’infiniment grand est une quantité à laquelle doit être attribué un nombre[103], nombre sur lequel il convient d’appliquer des opérations ordinaires[104]. Il en vient à penser ainsi à la suite de ses travaux en arithmétique et en trigonométrie ; il ne présuppose donc pas que l'infini ait différentes valeurs, il le découvre. Comme « des propriétés finies ne peuvent être prédiquées à tous les cas de l’infini »[105], il faut trouver les propriétés de l’infini. Subséquemment, ces propriétés seront élaborées dans sa théorie des ensembles des nombres transfinis.

La réflexion de Cantor le mène à fonder les mathématiques sur une théorie des ensembles plutôt que sur l’arithmétique[99]. Il s’inspire ainsi de la démarche de Bolzano[106] et de sa méthode de la correspondance biunivoque, ou bijection. Cantor considère donc les ensembles comme des objets ayant « une existence en soi indépendamment de nos moyens de l’atteindre »[107] et seulement définis par leur contenu. Cantor travaillera essentiellement avec les ensembles infinis suivants :

• l'ensemble des nombres naturels N = {0, 1, 2, 3, ...} ;
• l'ensemble des nombres rationnels Q : les fractions, incluant les éléments de N ;
• l'ensemble des nombres réels R : Q, ainsi que les nombres avec une infinité de décimales irrégulières comme la racine carrée de 2, π ou e.

Les nombres réels intéresseront particulièrement Cantor puisqu’ils permettent de localiser n’importe quel point sur une droite, dans un plan, ou dans l'espace.

Comme un ensemble se définit par ses éléments, il faut trouver une façon de les compter pour pouvoir les comparer. C’est ici qu’intervient la notion de cardinalité : le nombre cardinal d’un ensemble est le nombre d’éléments contenus dans cet ensemble[108] ; ceci « faisant abstraction de la nature des éléments de l’ensemble »[109]. Ainsi, dans l’ensemble {2, ..., 101}, la cardinalité est de 100. Dans le cas des nombres infinis, il faudra trouver une façon de les comptabiliser et de leur attribuer un cardinal. Cela sera possible en les comparant entre eux.

On peut ainsi chercher à comparer la cardinalité d'un ensemble avec celle de son ensemble des parties : il s'agit de l'ensemble des ensembles possibles, à l'intérieur d'un ensemble. Par exemple, si le cardinal de A = {1, 2, 3} est 3, celui de son ensemble des parties est 2³ = 8, car on peut former 8 ensembles à partir de A : {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}, ∅.

Pour comparer les ensembles finis, il s’agit de les compter, ce qui n’est rien d’autre que les associer un à un à l’ensemble M des nombres {1, 2, 3, …, n} où n est le nombre d’éléments dans l’ensemble, autrement dit le nombre cardinal. On cherche à établir entre eux une correspondance biunivoque ou bijection, c’est-à-dire une association de tous les éléments d’un ensemble avec ceux d’un autre, « sans répétition ni omission »[110] ; si une telle correspondance est possible, on dira que les deux ensembles ont la même « puissance », ils sont équipotents[109]. En des termes plus précis, associer des éléments de l'ensemble D à ceux de l'ensemble E, sans répétition (pour chaque élément de D, il n'y a qu'un élément de E associé), est une simple injection, alors que les associer, sans oublier d'éléments de D, est une surjection. Une bijection n'est qu'une relation de deux ensembles qui est à la fois injective et surjective.

Une telle correspondance peut s’appliquer aux ensembles infinis. De ce fait, l’ensemble de tous les nombres naturels pairs peut être mis en association avec l’ensemble de tous les naturels par la fonction y = 2x, où x est un élément parmi l’ensemble N de tous les naturels et y un élément parmi l’ensemble N′ de tous les naturels pairs. La cardinalité de N et de N′ est donc la même, aussi contre-intuitif que cela puisse paraître.

Ainsi, à première vue, il semble y avoir davantage de réels que de rationnels, et de rationnels que de naturels[111] ; or, Cantor montre que les rationnels Q et les naturels N peuvent être mis en correspondance biunivoque, et donc qu’ils possèdent le même nombre d’éléments. Cela permettra en fait de ranger les nombres rationnels (considérés comme fractions) de la façon suivante : Q⁺ = {1/1, 2/1, 1/2, 3/1, 1/3, 3/2, 2/3, 4/1, 1/4, ...} (les fractions négatives ne sont pas incluses ici pour faciliter la compréhension). On remarquera que, dans la suite, les fractions réductibles, et donc répétitives, ont été retirées (2/4 = 1/2, par exemple). Comme les nombres rationnels sont placés dans un ordre qui les réunira tous sans exception, on peut dire qu’ils sont dénombrables, c’est-à-dire qu’on peut associer un nombre n à chacun d’eux. De manière plus générale, on voit que tout ensemble dénombrable infini a la même cardinalité, et donc le même nombre d’éléments que les naturels.

Les comparaisons entre N et N′ ou entre Q et N reviennent à envisager une partie comme aussi grande que le tout ; ce qui va à l’encontre de ce que les philosophes ont toujours considéré comme une règle fondamentale[112]. Cette apparente transgression chez Cantor devient finalement la définition d’un ensemble infini : la cardinalité d’un ensemble est infinie si et seulement si une ou plusieurs de ses parties est égale à son tout[note 3].

Or, tous les ensembles infinis n’ont pas la même cardinalité comme le montre l’argument de la diagonale, démonstration de l’impossibilité de dresser une bijection entre N et R, et donc que ${\displaystyle {\aleph _{0}}<2^{\aleph _{0}}}$, c'est-à-dire que la cardinalité des réels est strictement supérieure à celle des nombres naturels. En effet, l’ensemble R des réels n’est pas dénombrable, et Cantor nommera sa cardinalité : puissance du continu. L’ensemble des réels est un ensemble continu (par opposition à discret) puisqu’il regroupe tous les points d’une droite, d’un plan ou d’un graphique, sans « trous ».

Les « nombres transfinis » est l’appellation que donne Cantor aux nombres infinis correspondant aux différentes cardinalités des ensembles infinis en raison de la connotation négative liée au concept d’infini, comme s’il s’agissait d’un « incomplet » ou d’un « indéfini ». Les transfinis cantoriens sont de réels objets mathématiques, ils sont « en acte », étant donné que les ensembles, aussi infinis soient-ils, sont bien réels. Par convention, la cardinalité de N (qui est aussi celle de Z et de Q) est nommée Aleph 0, ${\displaystyle {\aleph _{0}}}$, et constitue la plus petite quantité infinie. « Aleph », qui est l'équivalent de la lettre « a » en hébreu, a sans doute été choisi parce que, pour Cantor, les infinis sont justement des entités réelles avec lesquelles on peut développer une nouvelle arithmétique[113]. Mais comment effectuer des calculs arithmétiques à partir de ${\displaystyle {\aleph _{0}}}$ ? Cantor démontre[114] que, pour tout entier ${\displaystyle {n}}$, « ${\displaystyle {\aleph _{0}+n=\aleph _{0}}}$ », que « ${\displaystyle {\aleph _{0}+\aleph _{0}=\aleph _{0}}}$ » et que « ${\displaystyle {\aleph _{0}\times \aleph _{0}=\aleph _{0}}}$ » .

Ce dernier résultat est déjà étonnant, car il implique l’assertion que l’ensemble des fractions et celui des entiers ont la même cardinalité. C'est d'ailleurs également le cas de l'ensemble des points d’une droite et de l’ensemble des points d’un plan, qui ont la même cardinalité, qui est cette fois celle du continu. En fait, peu importe le nombre de dimensions de la « zone de travail », le nombre de points qu’elle contient est identique. On a donc c × c = c où c est la cardinalité d’un ensemble transfini. Par conséquent, « les espaces d’un nombre arbitraire de dimensions peuvent être seulement cartographiés sur la ligne unidimensionnelle des réels »[115]. Dans sa correspondance avec Dedekind, Cantor dira à propos de cette découverte « je le vois, mais je ne le crois pas »[116].

On pourrait croire, d'après les résultats précédents, qu'il n'y aurait qu'une seule cardinalité infinie. Mais Cantor démontre (voir Théorème de Cantor pour une analyse détaillée) qu'il n'y a pas de surjection – et donc pas de bijection – entre un ensemble B et son ensemble des parties (P(B)). Cela est assez évident pour les ensembles finis, par contre, pour les infinis, il faut opérer une reduction ad absurdum et une construction (non effectuée ici). Le résultat auquel arrive Cantor est que, la cardinalité de N < la cardinalité de P(N) < celle de P(P(N))... la cardinalité de N est ${\displaystyle {\aleph _{0}}}$, alors que celle de son ensemble des parties est de ${\displaystyle 2^{\aleph _{0}}}$ etc. Ainsi, ${\displaystyle \aleph _{0}<2^{\aleph _{0}}<2^{2^{\aleph _{0}}}\ldots }$

Cependant, Cantor veut faire mieux que de dresser une telle hiérarchie : il veut construire la suite des alephs où chaque nouvel aleph est le successeur immédiat du précédent. Il aura besoin, pour ce faire, des ordinaux.

Cantor devra faire appel à la théorie des ordinaux, c'est-à-dire des ensembles en tant qu'ils sont ordonnés (où, contrairement aux cardinaux, la position des termes est primordiale). L'ordinalité ne peut être appliquée qu'à des ensembles bien ordonnés (qui ont un bon ordre). Cantor réussit ainsi à obtenir, grâce aux ordinaux, un langage plus précis, qui lui permettra d'avoir une arithmétique plus subtile des infinis. Ainsi, l'addition n'est pas commutative avec les ordinaux, par exemple ${\displaystyle \omega +1\neq 1+\omega }$ (${\displaystyle \omega }$ correspondant à l’ordinalité de ${\displaystyle \mathbb {N} }$). L'ordinalité permet également de comparer des ensembles avec plus de précision que par la simple comparaison de cardinalité.

Grâce à la notion d'ordinaux, Cantor réussit à définir les alephs : ${\displaystyle {\aleph _{0}}}$ est la cardinalité de l'ensemble – infini – de tous les ordinaux finis, alors que ${\displaystyle {\aleph _{1}}}$ est celle de tous les ordinaux dénombrables. Et en poursuivant il lui devient possible de construire la suite (elle-même indexée par les ordinaux) :

${\displaystyle {\aleph _{0}}<{\aleph _{1}}<{\aleph _{2}}<{\aleph _{3}}<\ldots <{\aleph _{\omega }}<\ldots }$.

Le cardinal de l'ensemble des ensembles d'entiers naturels est celui de l'ensemble des réels, et Cantor fait l'hypothèse que ce cardinal est ${\displaystyle {\aleph _{1}}}$ : c'est l'hypothèse du continu (le continu est l'ensemble des réels, qui n'a pas de « trous »). Cette dernière équivaut donc à soutenir que ${\displaystyle {\aleph _{1}}}$ = ${\displaystyle 2^{\aleph _{0}}}$, à savoir, que la cardinalité des réels est le successeur de celle de l'ensemble des entiers naturels, c'est-à-dire la « quantité infinie » immédiatement supérieure.

Malgré sa concession pour l’utilité de l’infiniment petit dans le calcul infinitésimal, Cantor s’oppose à ce que l’infiniment petit soit un véritable infini (en acte), autrement dit, qu’il soit un objet mathématique à part entière, et il le définira plutôt comme un « mode de variabilité »[117] ou un infini simplement potentiel. Il dira qu’il s’agit d’un infini « improprement dit »[99], dont la grandeur est variable, décroissante à volonté, mais toujours finie comme l’est n’importe quel nombre irrationnel (ce n’est pas parce qu’un nombre en particulier a un nombre infini de décimales sans règle qu’il est lui-même infini). Dans le Mitteilungen, Cantor souhaite montrer formellement la contradiction intrinsèque des infinitésimaux, mais il ne fait que réitérer finalement l’axiome d’Archimède (à partir de a et b où a < b, où a et b sont des nombres réels positifs, et où il existe un c tel que a×c > b)[118]. Cantor rejettera donc les théories de Du Bois-Reymond et de Thomae Stolz, ainsi que celle de Veronese, car elles échouent toujours à montrer à quel ensemble peuvent référer les infinitésimaux (ou de quels ensembles ils sont obtenus). Si les infinitésimaux étaient des nombres, ils devraient être constitutifs d’un ensemble, et ce dernier serait plus continu que l’ensemble des réels[119](lui-même « puissance du continu »).

Abordée dans le Mitteilungen, la question de l’infini absolu de Dieu est pour Cantor d’une importance capitale[120]. Même si elle concerne plus directement la théologie spéculative, elle sert tout de même de fondement à la théorie des transfinis[121]. C’est une sorte de révélation mystique pour Cantor : « il Lui a plu que je parvienne aux révélations les plus étonnantes et les plus inattendues dans la théorie des ensembles »[122], écrit-il à propos de ce qu’il considère comme un véritable infini, comme un maximum absolu. Les nombres transfinis sont accessibles à l’homme, mais leur ensemble, c’est-à-dire le système de tous les nombres « Ω »[123], est incompréhensible.

Comment concilier la diversité mathématique des infinis (aleph 0, 1, la puissance du continu, etc.) avec l’unicité de l’infinitude absolue de Dieu ? Pour Cantor, c’est ce dernier qui garantit l’existence des transfinis, car a priori, ils devraient normalement découler de la nature infinie de Dieu, et qu’a posteriori, ils permettent une explication d’un plus grand éventail de phénomènes. Malgré tout, il semble que la théorie cantorienne sur les transfinis puisse se passer de l’hypothèse de Dieu[122].

Bertrand Russell (1916).

L’infini devient un problème pour Russell (1872 Trellech (Monmouthshire, pays de Galles) - 1970) lui-même au cours de ses recherches avec Whitehead sur la réduction logique des mathématiques dans les Principia Mathematica de 1910 à 1913. Il propose peu de temps après une application de la méthode analytico-logique au problème traditionnel de l’infini en philosophie pour en dégager une théorie positive dans La Méthode scientifique en philosophie en 1914.

Le projet logiciste consiste à démontrer logiquement les concepts et les propositions mathématiques. En 1889, Peano développe une axiomatique de la théorie des nombres réduisant ainsi les mathématiques à l’arithmétique. Pour que Russell puisse démontrer la réductibilité des mathématiques à la logique pure, tout ce qu’il a à faire, c’est donc de réduire les axiomes de Peano à la logique[124]. Pour ce faire, il mobilise les outils conceptuels de Cantor en mathématique et de Frege en logique. Toutefois, ce projet s’avère être un échec car Russell n’arrive pas à démontrer logiquement l’existence d’une classe infinie d’objets et se voit dès lors obligé de postuler l'infinité d'objets qui la rend possible.

Russell travaille avec la définition frégéenne du nombre avancée dans Les fondements de l’arithmétique : « la classe de toutes les classes semblables à la classe donnée »[125]. Cette définition du nombre permet à Russell de fournir la démonstration logique de quatre des cinq axiomes de l’arithmétique de Peano. Seul l’axiome qui consiste à postuler que « si deux nombres ont le même successeur, ces deux nombres sont identiques »[126] est problématique. Le problème vient entre autres de la définition logique du nombre telle que donnée par Frege.

La définition logique du nombre considère celui-ci comme une propriété d’un terme général ou d’une description générale[127]. Selon Russell, dans le cas du nombre, il est possible de remplacer la notion de terme général par celle de classe sans que cela ne pose de problème sur le plan logique. Ainsi, n’importe quel nombre, en tant que prédicat d’un terme général qui dénote quelque chose qui n’existe pas, a pour cardinalité la classe nulle, car le nombre ne dénote rien[128]. Par exemple, zéro est un prédicat qui s’applique au terme général « licorne » car aucune licorne n’existe. Étant donné cette caractéristique du nombre, il faut nécessairement qu’il y ait une classe infinie afin qu’il soit possible de démontrer logiquement l'axiome de Peano. Sinon, tout nombre dépassant le dernier nombre qui dénote la quantité de tout ce qui existe a le même cardinal que son successeur, soit la classe nulle. Ces nombres sont donc identiques[129]. Si n est le nombre de choses qui existent, son successeur n+1 a une cardinalité de 0, de même que n+2. n+1 a donc pour successeur n+2 tout en lui étant identique, ce qui est une contradiction avec l'axiome de Peano. Afin qu’il n‘y ait pas de contradiction et que cet axiome puisse être démontré, il faut nécessairement qu’il y ait une classe infinie[129]. Russell considère donc trois possibilités de démontrer l’existence d’une classe infinie.

La première des classes infinies est dérivée d’un argument inspiré de Parménide, considérant l’Être[129]. La deuxième classe infinie est dérivée d’un argument tenant compte du nombre et de son idée[130]. Ces deux démonstrations sont invalides à cause de leur caractère psychologique et du fait que l’être et l’idée du nombre ne peuvent constituer des prémisses mathématiquement démontrables[130]. La dernière démonstration, contrairement aux deux autres, est dérivée d’un argument qui relève de la logique. L’argument démontre qu'il est possible de construire une classe infinie à partir de la classe nulle. 0 existe à cause de la classe nulle. 1 est le nombre de la classe dont seule la classe nulle est membre ; 2 est le nombre de la classe constiuée de 1 et 0, et ainsi de suite. En suivant ce principe, la classe spécifique à chaque nombre est construite. Le nombre de 0 à n est n+1 et ce dernier est un nombre fini. À cause de la caractéristique héréditaire des nombres, l’existence est une propriété de tous les nombres entiers finis. Ainsi tous les nombres entiers existent et la cardinalité de la suite des nombres finis est infinie. Toutefois, selon ce raisonnement chaque nombre sera d’un type différent que son successeur. Étant donné que cette preuve ne respecte pas la théorie des types, elle n’est pas valide. En n’arrivant pas à démontrer l’existence d’une classe infinie, Russell est forcé de postuler l’infini à titre d’axiome.

Cet axiome suppose l’infinité de l’univers du discours, car seulement ainsi il peut y avoir une classe infinie et une infinité de nombres. Cependant, le fait que cet axiome énonce un prédicat d’existence fait en sorte qu’il ne puisse appartenir à la logique pure[131]. Malgré le fait qu’il ne peut être démontré logiquement, Russell soutient que seul l’axiome de l’infini peut assurer l’applicabilité de la logique pure au monde empirique. À ce titre, puisque la logique est applicable au monde, l’axiome de l’infini constitue une hypothèse empiriquement vérifiable. Par ailleurs, l’axiome de l’infini semble problématique dans la mesure où il est posé de manière ad hoc dans la démonstration de Russell. Puisque ce dernier a foi en la vérification empirique de l’axiome, il le présuppose dans l’application de sa méthode analytico-logique en philosophie.

Zénon affirme que l’espace et le temps sont indivisibles en points et en instants dans les contextes fini et infini. Selon Russell, si l’espace et le temps consistent en un nombre fini de points et d’instants, alors les arguments de Zénon contre la thèse que l’espace et le temps sont composés de points et d’instants sont tout à fait valables[132]. En mathématique, le calcul infinitésimal est l’outil fondamental de l’étude des corps en mouvement dans l’espace en fonction du temps. Or, le calcul infinitésimal présuppose que l’espace et le temps ont une structure en points et en instants. Au sens de Zénon, le calcul infinitésimal est donc logiquement infondé. Or, Russell montre que si l’espace et le temps consistent en un nombre infini de points et d’instants, alors les paradoxes de Zénon n’ébranlent plus les mathématiques à cet égard[132]. Le présupposé essentiel du calcul infinitésimal conserve ainsi sa légitimité philosophique. Russell souligne cependant que la tradition a longtemps négligé la thèse selon laquelle le monde est composé d’un nombre infini de points et d’instants à cause des contradictions qu’impliquait une notion naïve de l’infini.

Pour illustrer les effets d’une conception erronée de l’infini, Russell analyse les deux premières antinomies de la raison pure de Kant sur l’idée régulatrice de monde[133].

Kant caractérise une série infinie par le fait qu’on ne peut jamais la synthétiser successivement au complet. Par extension, c’est affirmer que la série des nombres naturels, à savoir la somme des termes de la suite des entiers positifs à partir de zéro, est infinie parce qu’elle ne peut se compléter dans un temps fini par l'homme, qui est fini. Or, Russell soutient que la notion d’infini « est avant tout une propriété de classes, et n’est que secondairement applicable aux séries »[134]. C'est qu'une série, par définition, tient compte de l’ordre successif des éléments la constituant de sorte qu’il y a toujours au moins un élément qui lui échappe lorsqu’elle est infinie. Au contraire, à la manière d'un concept, une classe renvoie à chacun des éléments la constituant, ce qui permet de capturer l’infini mathématique sans en avoir fait la synthèse. Russell fait ressortir par là l’erreur consistant à comprendre l’infini à partir de notre propre finitude au lieu de le considérer comme le caractère propre du nombre en tant qu’objet logico-mathématique.

Kant plaide en faveur de l’impossibilité d’un espace composé de points en raison de l’absurdité qu’implique la division à l’infini. En fait, Kant suppose que pour obtenir un point, il faudrait arriver au bout d’une opération de découpages successifs, à chaque fois en deux, de l’espace qui par définition est sans fin. Or, pour éviter ce problème, Russell conçoit à l’instar de Frege et de Cantor que « tout comme une classe infinie peut intégralement être donnée par le concept qui la définit, […] de même un groupe infini de points peut être donné intégralement comme formant une ligne, une aire ou un volume, quoiqu’ils ne puissent jamais être atteints par des divisions successives »[135].

Comme le suggère Leibniz, un infinitésimal serait une quantité d’espace ou de temps si petite qu’il n’en existerait pas une inférieure de sorte qu’il serait impossible de la diviser en deux quantités finies. Or, Russell rejette la possibilité en mathématique de manipuler des quantités infinitésimales, à savoir des quantités telles que « toute distance finie quelconque lui soit supérieure »[136]. Selon Russell, l’erreur d’imagination menant à la croyance des infinitésimaux consiste à penser que, à la fin de l’opération de découpage en deux de l’espace et du temps, les distances et les périodes ne soient plus divisibles en quantités finies. De là, il existerait des quantités infiniment petites manipulables en mathématique. Or, Russell rappelle que la divisibilité infinie ne permet pas de conclure à l’existence d’un dernier terme dans une opération qui par définition est sans fin[137].

Russell explicite en ce sens l’erreur logique consistant à interpréter l’énoncé vrai « pour toute distance finie[note 4], il y a une distance inférieure » par l’énoncé faux « il y a une distance telle que, quelque distance finie que nous puissions choisir, la distance en question est inférieure »[137]. Du point de vue de la logique formelle, il s’agit là d’une inversion des quantificateurs universel et existentiel opérant dans la proposition. En effet, la proposition fausse veut faire dire « il existe une distance plus petite que toute distance finie », l’infinitésimal, alors que la proposition vraie veut dire « pour toutes distances, il existe une distance finie plus petite », ce qui implique l’impossibilité de l’infinitésimal. Par la méthode analytico-logique, Russell parvient donc à mettre de l’ordre dans la compréhension des infinitésimaux en vue de rejeter leur nécessité pour opérationnaliser le calcul infinitésimal.

Pour la grande majorité des mathématiciens du XXI^e siècle, l'infini (dans chacune de ses acceptions) est une notion mathématique comme les autres, possédant une définition explicite, et qui pourrait en principe se ramener aux objets primitifs du langage utilisé (le plus souvent celui de la théorie des ensembles de Zermelo-Fraenkel). Ainsi, par exemple, un ensemble est infini (au sens de Dedekind) s'il peut être mis en bijection avec un de ses sous-ensembles stricts ; le point à l'infini d'un espace est un objet formel ajouté à cet espace en suivant des règles précises, etc. Les sections suivantes détaillent les différents usages de cette notion, et précisent d'éventuels points de désaccord.

L'un des objectifs de la théorie de Cantor est de donner un sens précis à la phrase « l'ensemble E contient un nombre infini d'éléments », et permettant en particulier de différencier plusieurs infinis différents (infini dénombrable, infini du continu, etc.). Comme cela a été exposé dans la partie historique, les conceptions de Cantor se sont heurtées, d'une part aux objections de certains mathématiciens, en particulier Kronecker, refusant l'« infini actuel », d'autre part aux contradictions bien réelles créées par une vision trop naïve de la théorie, en particulier par l'« ensemble de tous les ensembles ». La solution à ces antinomies, et à la crise des fondements qui en résultait, fut apportée par diverses axiomatiques (le plus souvent équivalentes entre elles), dont la plus utilisée est celle de Zermelo-Fraenkel, dite ZF. Pour ces axiomatiques, il existe évidemment (au sens intuitif) des « collections d'objets » infinies (par exemple la collection de tous les entiers) ; l'axiome de l'infini affirme alors que l'une de ces collections au moins est un ensemble (et donc un objet légal de la théorie, contrairement à la collection de tous les ensembles), ce qui revient à affirmer l'existence de l'infini actuel. La hiérarchie d'infinis découverte par Cantor devient alors une simple conséquence de la théorie, et l'existence de cardinaux distincts ne présente plus de difficulté de principe ; cependant la question de leur taille exacte fait depuis cette époque l'objet d'intenses recherches, portant en particulier sur l'hypothèse du continu et sur les conséquences de l'existence de certains grands cardinaux. La définition précise d'un « ensemble de taille infinie » s'avère toutefois dépendre de l'axiome du choix : en sa présence (c'est-à-dire dans la théorie ZFC), toutes ces définitions sont équivalentes, mais sinon, il est par exemple possible de construire des ensembles infinis ne contenant aucune suite dénombrable d'objets distincts (ensembles dits finis au sens de Dedekind). Enfin, cette théorie permet un véritable « calcul avec l'infini », que ce soit avec les nombres cardinaux mesurant la taille des ensembles, ou avec les nombres ordinaux, plus précis, et décrivant, en un certain sens, une façon de « compter » les éléments des ensembles étudiés.

Le sens à donner à l'infini (infiniment grand ou infiniment petit) en analyse a amené aux querelles philosophiques du XVII^e siècle[138], puis, après d'impressionnants succès initiaux, à de sérieuses difficultés mathématiques, liées en particulier à l'impossibilité de construire un système rigoureux d'infinitésimaux. Le travail de refondation de Cauchy et Weierstrass dans la première moitié du XIX^e siècle devait amener à remplacer partout des phrases telles que « la dérivée de f en zéro est infiniment proche du quotient ${\displaystyle f(h)-f(0) \over h}$ lorsque h est infiniment petit » par ${\displaystyle f'(0)=\lim _{h\to 0}{f(h)-f(0) \over h}}$, la notion de limite recevant elle même une définition parfaitement rigoureuse, et ne faisant plus intervenir que des nombres ordinaires ; dans ce contexte, le symbole ${\displaystyle \infty }$ dans des notations telles que ${\displaystyle \lim _{x\to +\infty }{4x^{2}+x \over 2x^{2}-1}=2}$ n'est plus qu'une abréviation. Avec ce choix, les infinis apparaissant en analyse ne sont que des infinis potentiels, ce que montrent bien les définitions classiques de Weierstrass, avec lesquelles la formule précédente se lit « l'expression ${\displaystyle {4x^{2}+x \over 2x^{2}-1}}$ peut être rendue aussi proche que l'on veut de 2 en prenant x suffisamment grand ».

Un point de vue plus moderne (mais mathématiquement strictement équivalent) consiste à rajouter aux ensembles de nombres étudiés de nouveaux éléments (comme pour la construction des nombres complexes), obtenant par exemple la droite réelle achevée ℝ ${\displaystyle =[-\infty ,+\infty ]}$ ; les nouveaux objets ${\displaystyle -\infty }$ et ${\displaystyle +\infty }$ sont munis de règles de calcul, telles que ${\displaystyle +\infty /2=+\infty }$, qui reflètent le calcul élémentaire sur les limites.

Des tentatives de redonner un sens aux infinitésimaux et à différents « ordres d'infinis » (pour pouvoir, par exemple, exprimer que le carré de l'infini est beaucoup plus grand que l'infini) ont été effectuées par du Bois-Reymond, Hardy et Landau ; elles consistent à introduire des fonctions de référence (les échelles de comparaison) et à dire par exemple qu'une quantité varie dans certaines conditions comme un infiniment petit de tel ou tel ordre si elle est équivalente à une des fonctions de l'échelle, elle-même très petite dans les mêmes conditions. Mais ces définitions, bien qu'utiles en pratique, souffrent d'un certain arbitraire, et sont par ailleurs nécessairement incomplètes (il existe toujours des fonctions situées en dehors d'une échelle donnée).

Les progrès de la logique mathématique dans la première moitié du XX^e siècle ont amené divers théoriciens (Hewitt, Robinson et Nelson en particulier) à envisager de reconstruire une théorie rigoureuse des infinitésimaux en s'appuyant sur la théorie des modèles. Dans cette approche, on construit par exemple un modèle des nombres réels « non standard », qui contient tous les réels ordinaires (comme ${\displaystyle \pi }$ ou ${\displaystyle {\sqrt {2}}}$) mais aussi de nouveaux nombres, nécessairement « infiniment grands » ou « infiniment proches » des anciens ; les résultats de la théorie garantissent que ces nouveaux réels ont toutes les propriétés des anciens (les paradoxes apparents, comme celui du plus petit entier non standard, qui avaient amené l'abandon de ces conceptions au XIX^e siècle, se résolvant par l'impossibilité d'exprimer certaines propriétés dans le langage précis utilisé).

L'intérêt principal de l'analyse non standard est de redonner un sens précis à de nombreuses formulations anciennes des concepts du calcul infinitésimal (dérivées, intégrales, sommes de séries, produits infinis, etc.), plus intuitives que l'approche moderne par calcul de limites, mais tombées en disgrâce car utilisant des notions d'infini non définies : ainsi, la définition de l'intégrale de Riemann devient simplement « le réel standard le plus proche d'une somme de Riemann ayant un pas infiniment petit ».

Une toute autre approche utilise les nombres surréels découverts par John Horton Conway : il s'agit d'une vaste extension des nombres réels à l'aide d'une ingénieuse application de la méthode des coupures de Dedekind, introduisant des nombres infinis tels que les ordinaux (avec ses notations, on a ${\displaystyle \omega =\left\{\left\{0,1,2,3,\cdots \right\}|\right\}=\left\{\mathbb {N} |\right\}}$) et permettant ensuite de calculer avec ces nombres comme avec des réels ordinaires, définissant ainsi des infiniment petits tels que ${\displaystyle \epsilon =\left\{0|\left\{1,{1 \over 2},{1 \over 3},\cdots \right\}\right\}=1/\omega }$, mais aussi des objets bien plus surprenants tels que ${\displaystyle \omega ^{1/\omega }}$, qui est infiniment grand, mais beaucoup plus petit que ${\displaystyle {\sqrt {\omega }}}$, par exemple. Il ne semble cependant pas que cette extension, en dépit de sa richesse, permette d'aborder des questions d'analyse non élémentaires.

La notion de point à l'infini, apparue avec le développement de la géométrie projective (elle-même développée en relation avec l'invention de la perspective géométrique), et ayant pour but de modéliser la phrase bien connue selon laquelle « les parallèles se coupent à l'infini », est désormais formalisée en géométrie par la construction des espaces projectifs.

Au début du XX^e siècle, la physique se trouvait dans l'impossibilité d'expliquer divers phénomènes[139], dont le fait qu'un corps noir à l'équilibre thermodynamique est censé rayonner un flux infini (voir catastrophe ultraviolette). Ce problème fut résolu par l'introduction des quanta par Planck, ce qui forme la base de la physique quantique.

Dans le cadre de la relativité générale, le Big Bang conduit, dans son interprétation naïve, à l'apparition de valeurs infinies (on parle aussi de singularités) à l'origine des temps, apportant ainsi la preuve que nos connaissances physiques actuelles ne sont pas capables de décrire cette époque lointaine de l'histoire de l'Univers.

Dans plusieurs branches de la physique, comme la théorie quantique des champs ou la physique statistique, les chercheurs ont pu éliminer les divergences indésirables de la théorie à l'aide de techniques mathématiques de renormalisation. Ces techniques n'ont pu être appliquées pour l'instant à la théorie de la gravitation.

• Axiome de l'infini
• Hôtel de Hilbert

• Voyages au pays des maths

• Lampe de Thomson
• Régression à l'infini
• L'Infini (œuvre et revue littéraire)

• Notices d'autorité :

  • GND
  • Japon
• Ressource relative à la recherche :
  • (en) Stanford Encyclopedia of Philosophy
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Universalis