Surjection
En mathématiques, une surjection ou application surjective est une application pour laquelle tout élément de l'ensemble d'arrivée a au moins un antécédent, c'est-à-dire est image d'au moins un élément de l'ensemble de départ. Il est équivalent de dire que l'ensemble image est égal à l'ensemble d'arrivée.
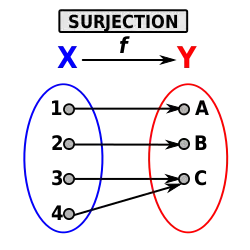
Il est possible d'appliquer l'adjectif « surjectif » à une fonction (voire à une correspondance) dont le domaine de définition n'est pas tout l'ensemble de départ, mais en général le terme « surjection » est réservé aux applications (qui sont définies sur tout leur ensemble de départ), auxquelles nous nous limiterons dans cet article (pour plus de détails, voir le paragraphe « Fonction et application » de l'article « Application »).
Pour désigner les ensembles de départ et d'arrivée d'une surjection, il est usuel de dire « de A sur B » au lieu de « de A dans B » comme pour une application en général.
Dans le cas d'une fonction réelle d'une variable réelle, sa surjectivité est équivalente au fait que son graphe intersecte toute droite parallèle à l'axe des abscisses.
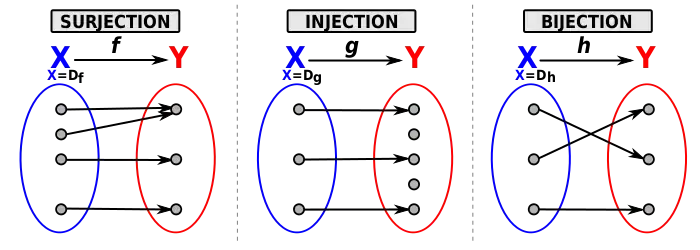
Une application qui est à la fois surjective et injective est une bijection.
Définition formelle
Une application f de X dans Y est dite surjective si pour tout élément y de Y, il existe au moins un élément x de X tel que f(x) = y, ce qui s'écrit formellement :
- .
Exemples
Exemple concret
On considère le cas d'une station de vacances où un groupe de touristes doit être logé dans un hôtel. Chaque façon de répartir ces touristes dans les chambres de l'hôtel peut être représentée par une application de l'ensemble X des touristes vers l'ensemble Y des chambres (à chaque touriste est associée une chambre).
- L'hôtelier souhaite que l'application soit surjective, c'est-à-dire que chaque chambre soit occupée. Cela n'est possible que s'il y a au moins autant de touristes que de chambres (dans ce cas, plusieurs touristes peuvent occuper la même chambre).
- Les touristes souhaitent que l'application soit injective, c'est-à-dire que chacun d'entre eux ait une chambre individuelle. Cela n'est possible que si le nombre de touristes ne dépasse pas le nombre de chambres.
- Ces souhaits ne sont compatibles que si le nombre de touristes est égal au nombre de chambres. Dans ce cas, il sera possible de répartir les touristes de telle sorte qu'il y en ait un seul par chambre, et que toutes les chambres soient occupées : l'application sera alors à la fois injective et surjective ; on dira qu'elle est bijective.
Exemples et contre-exemples dans les fonctions réelles
La fonction définie par
n'est pas surjective car certains réels ne possèdent pas d'antécédent. Par exemple, il n'y a pas de réel x tel que f(x) = −4. Mais si on change la définition de f en donnant comme ensemble d'arrivée ℝ+,
alors elle le devient car chaque réel positif possède au moins un antécédent : 0 possède exactement un antécédent, 0, et tous les réels y strictement positifs en possèdent deux, la racine carrée de y et son opposé.
La fonction définie par
est surjective puisque, pour tout réel arbitraire y, il existe des solutions à l'équation y = 2x + 1 d'inconnue x ; une solution est x = (y − 1) / 2.
La fonction définie par
n'est pas surjective car les réels strictement plus grands que 1 ou strictement plus petits que –1 n'ont pas d'antécédent. Mais la fonction définie par
qui possède la même expression que g, mais avec un ensemble d'arrivée qui a été restreint à l'ensemble des réels compris entre –1 et 1, est surjective. En effet, pour tout réel arbitraire y de l'intervalle [–1, 1], il existe des solutions à l'équation y = cos(x) d'inconnue x : ce sont les réels x = ±arccos(y) + 2kπ pour tout entier relatif k.
Sur ces quelques exemples, on voit qu'il est toujours possible de transformer une application non surjective en une surjection à condition de restreindre son ensemble d'arrivée.
Propriétés
Réduction de l'ensemble d'arrivée
Si f est une application de X dans Y et Im(f) = f(X) son ensemble image (c'est-à-dire l'ensemble des images par f des éléments de X), alors l'application
est une surjection.
En d'autres termes, si f est corestreinte à Im(f), c'est-à-dire si on remplace son ensemble d'arrivée par son ensemble image, elle devient surjective.
Décomposition canonique
Toute application f peut être décomposée comme f = i∘s où s est une surjection et i une injection. Cette décomposition est unique à un isomorphisme près. Une décomposition est fournie dans le paragraphe détaillé. Une autre (équivalente) est de choisir pour s la surjection définie ci-dessus, et pour i l'injection canonique de l'image de f dans son ensemble d'arrivée.
Images directes et réciproques
Pour toute application f : X → Y, les quatre propriétés suivantes sont équivalentes[1] :
- f est surjective ;
- tout sous-ensemble B de Y est l'image directe de son image réciproque, c.-à-d. f(f −1(B)) = B ;
- f(f −1(Y)) = Y ;
- pour toute partie A de X, le complémentaire de l'image directe de A est inclus dans l'image directe du complémentaire de A, c.-à-d. Y\f(A) ⊂ f(X\A).
Surjectivité et composée
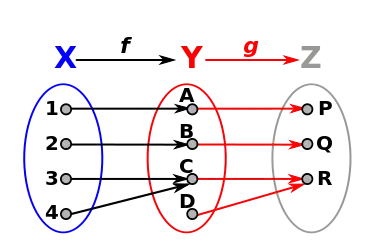
Soit f une application de X dans Y.
- Pour toute application g de Y dans Z[1] :
- si g∘f est surjective alors g est surjective ;
- si f et g sont surjectives alors g∘f est surjective ;
- si g est injective et si g∘f est surjective alors f est surjective.
- f est surjective si et seulement si, pour tout Z et pour toutes applications g et h de Y dans Z, g∘f = h∘f entraîne g = h[1]. En d'autres termes, les surjections sont précisément les épimorphismes dans la catégorie des ensembles.
Section et axiome du choix
Soit f une application de X dans Y. Si f est « inversible à droite », c'est-à-dire[2] s'il existe une application g de Y dans X telle que la fonction composée f∘g soit égale à l'application identité sur Y, alors f est surjective (d'après une propriété vue plus haut).
Une telle application g est appelée une section, ou inverse à droite[3] de f. Elle est nécessairement injective.
Réciproquement, si f est surjective alors elle admet une section. Cette propriété s'appuie sur le fait que l'on peut toujours « remonter les flèches » de Y vers X . Elle est toujours vraie si Y est fini. L'affirmation[4] qu'elle est vraie pour tout ensemble Y est équivalente à l'axiome du choix[5].
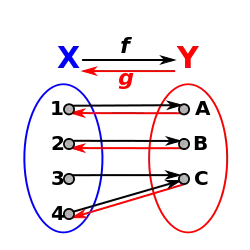 Construction d'une fonction g. |
 f∘g = Identité dans Y. |
Cardinaux
- S'il existe une surjection de X dans Y, alors (d'après ce qui précède, donc en admettant l'axiome du choix) il existe une injection de Y dans X, autrement dit l'ensemble X a au moins autant d'éléments que l'ensemble Y, au sens des cardinaux.
- Théorème de Cantor (sans axiome du choix) : pour tout ensemble X, il n'existe aucune surjection de X dans l'ensemble de ses parties.
Dénombrement des surjections dans le cas fini
Le nombre de surjections d'un ensemble à n éléments sur un ensemble à p éléments est égal à :
où est le nombre de Stirling de seconde espèce.
Ceci peut se démontrer par la formule d'inversion de Pascal, ou le principe d'inclusion-exclusion.
Notes et références
- Voir par exemple .
- Lucien Chambadal et Jean-Louis Ovaert, Cours de mathématiques, vol. 1 : Notions fondamentales d'algèbre et d'analyse, Gauthier-Villars, , p. 27.
- N. Bourbaki, Éléments de mathématique : Théorie des ensembles [détail des éditions], p. II-19 sur Google Livres.
- Bourbaki, p. II-18, la démontre en utilisant une forme plus forte que l'axiome du choix.
- Saunders Mac Lane, Garrett Birkhoff et Jean Weil, Algèbre et solutions développées des exercices : structures fondamentales, les grands théorèmes, théorie de Galois, J. Gabay, (ISBN 2-87647-138-8 et 978-2-87647-138-2, OCLC 490130463), p. 11





![{\begin{matrix}h:&\mathbb{R} &\rightarrow &[-1,1]\\&x&\mapsto &\cos(x)\\\end{matrix}}](https://img.franco.wiki/i/1b57386cbbea6126e4ab97b483a6d82470daccc0.svg)


