Arc cosinus

En mathématiques, l’arc cosinus d'un nombre réel compris au sens large entre −1 et 1 est l'unique mesure d'angle dont le cosinus vaut ce nombre, entre l'angle nul et l'angle plat.

Fonction arc cosinus

Représentation graphique (dans un repère non normé).

Notation	$\arccos(x)$
Réciproque	$\cos(x)$ sur [0 ; π]
Dérivée	${\frac {-1}{\sqrt {1-x^{2}}}}$
Primitives	$x\,\arccos(x)-{\sqrt {1-x^{2}}}+C$

Principales caractéristiques
Ensemble de définition	[−1 ; 1]
Ensemble image	[0 ; π]

La fonction qui associe à tout nombre réel compris au sens large entre −1 et 1 la valeur de son arc cosinus en radians est notée arccos (Arccos[1] ou Acos en notation française, et cos⁻¹, parfois acos ou acs, en notation anglo-saxonne).

Il s'agit alors de la réciproque de la fonction trigonométrique cosinus sur l'intervalle [0, π] donc, dans un repère cartésien orthonormé du plan, la courbe représentative de arc cosinus s'obtient à partir de la courbe de la restriction du cosinus par la symétrie d'axe la droite d'équation y = x.

Définition

La fonction ${\displaystyle \arccos$ est définie comme la fonction réciproque de $\cos$ sur $[0,\pi ]$ , c'est-à-dire qu'il s'agit de l'unique fonction telle que :

\forall x\in [0,\pi ]\quad \arccos(\cos x)=x.

Propriétés

Non parité

Contrairement aux fonctions Arc sinus et Arc tangente, la fonction $\arccos$ n'admet aucune parité. En revanche, elle possède la propriété suivante :

\forall x\in [-1,1]\quad \arccos(-x)=\pi -\arccos x.

Relation avec le sinus

Pour $X=\arccos x$ , on a $\sin X\geq 0$ (car $X\in [0,\pi ]$ ) et $\cos ^{2}X+\sin ^{2}X=1$ , donc

\sin(\arccos x)={\sqrt {1-x^{2}}}.

« Inversion » des formules trigonométriques

Partant de n'importe quelle formule trigonométrique, on peut « l'inverser », obtenant une relation entre valeurs des fonctions réciproques, mais qui ne sera le plus souvent valable que dans des intervalles restreints. Par exemple, puisque $\cos 2x=2\cos ^{2}x-1$ , on aura $\arccos(2X^{2}-1)=2\arccos X$ , mais seulement pour $X\in [0,1].$

Dérivée

Comme dérivée d'une fonction réciproque, $arccos$ est dérivable sur $]-1,1[$ et vérifie

\arccos '(x)={\frac {-1}{\sqrt {1-x^{2}}}}.

Cette formule s'obtient grâce au théorème sur la dérivée d'une fonction réciproque et à la relation avec le sinus (voir supra).

Forme intégrale indéfinie

Cette fonction peut s'écrire sous la forme d'une intégrale indéfinie :

\arccos x=\int _{1}^{x}-{\frac {1}{\sqrt {1-t^{2}}}}\,\mathrm {d} t.

Primitives

Les primitives de la fonction arccos s'obtiennent par intégration par parties :

\int \arccos(x)~\mathrm {d} x=x\,\arccos(x)-{\sqrt {1-x^{2}}}+C.

Relation entre arc cosinus et arc sinus

arccos(x) (bleu) et arcsin(x) (rouge)

\arccos x+\arcsin x={\frac {\pi }{2}}

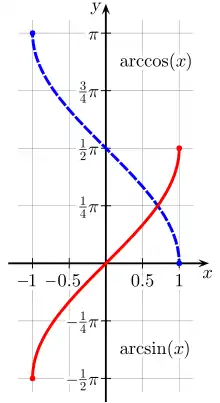
En effet, $π / 2$ – $arccos x$ est compris entre – $π / 2$ et $π / 2$ et son sinus est égal au cosinus de $arccos x$ c'est-à-dire à $x$ , donc $π / 2$ – $arccos x$ = $arcsin x$ .

(Pour une autre méthode, voir le § « Monotonie et signe de la dérivée » de l'article sur les fonctions monotones.)

Forme logarithmique complexe

On peut exprimer la fonction arccos à l’aide du logarithme complexe :

\arccos(x)=-\mathrm {i} \,\ln \left(x+\mathrm {i} \,{\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}\,+\mathrm {i} \ln \left(\mathrm {i} \,x+{\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}-\arcsin(x).

Référence

Notation issue du programme de mathématiques en CPGE, p. 10.

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.