Radian
Le radian (symbole : rad) est l'unité d'angle (plan ou dièdre) du Système international.
| Radian | |
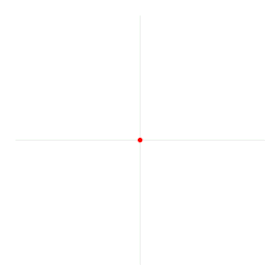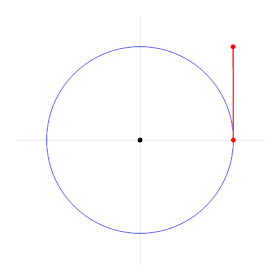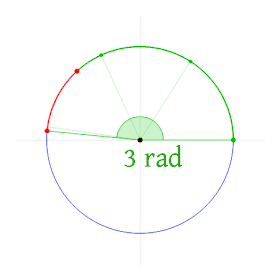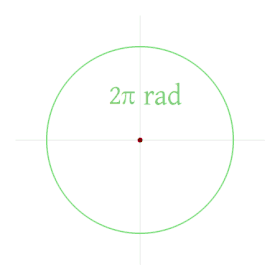 Définition de l'angle en radians. | |
| Informations | |
|---|---|
| Système | Unités dérivées du Système international |
| Unité de… | Angle plan |
| Symbole | rad |
| Conversions | |
| 1 rad en... | est égal à... |
| tour complet | 2π rad |
Par définition, un angle ayant son sommet au centre d'un cercle a une mesure d'un radian s'il intercepte, sur la circonférence de ce cercle, un arc d'une longueur égale à celle du rayon du cercle.
Bien que le mot « radian » ait été inventé au cours des années 1870 par Thomas Muir et James Thomson[1] - [2], les mathématiciens mesuraient depuis longtemps les angles en prenant pour unité le rapport entre la circonférence et la longueur du rayon.
Définition
Considérons un secteur angulaire, formé de deux droites concourantes distinctes, et un cercle de rayon r tracé dans un plan contenant ces deux droites, dont le centre est le point d'intersection des droites. Alors, la valeur de l'angle en radians est le rapport entre la longueur L de l'arc de cercle intercepté par les droites et le rayon r.

Un angle d'un radian intercepte sur la circonférence de ce cercle un arc d'une longueur égale au rayon. Un cercle complet représente un angle de 2π radians, appelé angle plein.
L'utilisation des radians est impérative lorsque l'on dérive ou intègre une fonction trigonométrique ou encore lorsque l'on utilise un développement limité de cette fonction trigonométrique : en effet, l'angle pouvant se retrouver en facteur, seule la valeur en radians a un sens. De ce fait, le calcul des fonctions trigonométriques par une série de Taylor suppose l'expression des angles en radians, tout comme l'application de la formule d'Euler, qui l'a posée en spécifiant que les angles devaient être mesurés par la longueur en rayons de l'arc qu'ils interceptent, plus d'un siècle avant l'invention du terme radian.
Petits angles
Pour les petits angles exprimés en radians, sin x ≈ tan x ≈ x.
- Pour un angle de valeur inférieure à 0,17 radian (soit ~10°), l'erreur est de moins de 1 % ;
- Pour un angle de valeur inférieure à 0,05 radian (soit ~3°), l'erreur est de moins de 0,1 %[3].
Dans le domaine de la topographie, où on traite d'angles faibles, on utilise le mil angulaire, une unité pratique, définie comme l'angle qu'intercepte une longueur de 1 mm à une distance de 1 m. Elle sert, par exemple, à déterminer la distance d'une mire de hauteur connue par la mesure de sa taille apparente. Dans les conditions où elle sert, cette unité s'identifie avec un milliradian.
Relations entre grades, degrés et radians

Un tour complet équivaut à 2π radians, 360 degrés, 400 grades.
Par conséquent,
- Un radian vaut environ 57,3° ou 57° 18' (360°÷2π) ;
- un degré vaut approximativement 17,5 milliradians.
Les formules de conversion entre les degrés et les radians sont :
- .
- .
Les formules de conversion entre les grades et les radians sont :
- .
- .
| nom de l'angle | valeur en radians (rad) | valeur en degrés (°) | valeur en tours (tr) | valeur en grades (gon) |
|---|---|---|---|---|
| angle nul | 0 rad | 0° | 0 tr | 0 gon |
| milliradian | 0,001 | 0,0573° ou 0° 3′ 26″ 16‴ | 0,00015915494 tr | 0,063 661 977 gon |
| π/6 rad | 30° | 0,08333 tr (1/12 tr) | 33,333 333 gon | |
| π/4 rad | 45° | 0,125 tr (1/8 tr) | 50 gon | |
| radian | 1 rad | 57° 17′ 44″ 48‴ | 0,1591549430919 tr (1/π/2 tr) | 63,661 980 gon |
| π/3 rad | 60° | 0,1666 tr (1/6 tr) | 66,666 666 gon | |
| angle droit | π/2 rad | 90° | 0,25 tr | 100 gon |
| 2π/3 rad | 120° | 0,333 tr | 133,333 333 gon | |
| 3π/4 rad | 135° | 0,375 tr | 150 gon | |
| angle plat | π rad | 180° | 0,5 tr | 200 gon |
| 5π/4 rad | 225° | 0,625 tr | 250 gon | |
| 3π/2 rad | 270° | 0,75 tr | 300 gon | |
| 7π/4 rad | 315° | 0,875 tr | 350 gon | |
| angle plein | 2π rad | 360° | 1 tr | 400 gon |
Voir aussi
Bibliographie
- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Bruxelles, De Boeck, , 976 p. (ISBN 9782807307445), « Radian »
Articles connexes
Notes et références
- (en) A.R. Crathorne, « The Word "Radian" », The American Mathematical Monthly, vol. 19, nos 10-11, , p. 166 (DOI 10.2307/2971878, JSTOR 2971878).
- (en) Robert J. Whitaker, « Whence the ‘‘Radian’’? », The Physics Teacher (en), vol. 32, no 7, , p. 444–445 (DOI 10.1119/1.2344073).
- Taillet, Villain et Febvre 2013, p. 39.




