Arc sinus

En mathématiques, l’arc sinus d'un nombre réel compris (au sens large) entre $-1$ et $1$ est l'unique mesure d'angle en radians dont le sinus vaut ce nombre, et comprise entre $-π/2$ et $π/2$ .

Fonction arc sinus

Représentation graphique de la fonction arc sinus.

Notation	$\arcsin(x)$
Réciproque	$\sin(x)$ sur $\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$
Dérivée	${\frac {1}{\sqrt {1-x^{2}}}}$
Primitives	$x\arcsin(x)+{\sqrt {1-x^{2}}}+C$

Principales caractéristiques
Ensemble de définition	[−1, 1]
Ensemble image	$\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$
Parité	impaire

La fonction qui associe à tout nombre réel compris au sens large entre $-1$ et $1$ la valeur de son arc sinus est notée arcsin (Arcsin[1] ou Asin en notation française, sin⁻¹, asin ou asn en notation anglo-saxonne). Il s'agit alors de la bijection réciproque de la restriction de la fonction trigonométrique sinus à l'intervalle $[-π/2, π/2]$ . Elle fait partie des fonctions circulaires réciproques.

On a donc par définition :

$\left\{{\begin{array}{c}\theta =\arcsin x\\x\in \lbrack -1,1]\end{array}}\right.\Leftrightarrow \left\{{\begin{array}{c}x=\sin \theta \\\theta \in \left[-{\dfrac {\pi }{2}},{\dfrac {\pi }{2}}\right]\end{array}}\right.$

Courbe représentative

Dans un repère cartésien orthonormé du plan, la courbe représentative de la fonction arc sinus est obtenue à partir de la courbe représentative de la restriction de la fonction sinus à l'intervalle $[-π/2, π/2]$ par la réflexion d'axe la droite d'équation $y = x$ .

Relations avec les fonctions circulaires directes

$\sin(\arcsin x)=x$ pour $x\in \lbrack -1,1]$
$\cos(\arcsin x)={\sqrt {1-x^{2}}}$ pour $x\in \lbrack -1,1]$
$\tan(\arcsin x)={\frac {x}{\sqrt {1-x^{2}}}}$ pour $x\in ]-1,1[$

Par contre, $\arcsin(\sin x)=x$ seulement pour $x\in \left[-{\dfrac {\pi }{2}},{\dfrac {\pi }{2}}\right]$

La formule générale est $\arcsin(\sin x)=(-1)^{k}(x-k\pi )$ où $k$ est la partie entière de ${\frac {x}{\pi }}+{\frac {1}{2}}$ .

Dérivée

Comme dérivée d'une bijection réciproque, arcsin est dérivable sur $]-1, 1[$ et vérifie $\arcsin 'x={\frac {1}{\sqrt {1-x^{2}}}}$ .Cette formule s'obtient grâce au théorème sur la dérivée d'une bijection réciproque et à la relation $\cos(\arcsin x)={\sqrt {1-x^{2}}}$ .

Développement en série entière

Si $|x|\leqslant 1$ ,

{\begin{aligned}\arcsin x&=x+{\frac {1}{2}}\cdot {\frac {x^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {x^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {x^{7}}{7}}+\dots \\&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}\cdot {\frac {x^{2n+1}}{2n+1}}\\&=\sum _{n=0}^{\infty }{\frac {{\binom {2n}{n}}x^{2n+1}}{4^{n}(2n+1)}}.\end{aligned}}

(Voir aussi Fonction hypergéométrique#Cas particuliers.)

Démonstration

Le développement de la dérivée est :

{\begin{aligned}\arcsin '(x)&=(1-x^{2})^{-{\frac {1}{2}}}\\&=1+\left(-{\frac {1}{2}}\right)(-x^{2})+{\frac {\left(-{\frac {1}{2}}\right)\left(-{\frac {3}{2}}\right)}{2}}(-x^{2})^{2}+{\frac {\left(-{\frac {1}{2}}\right)\left(-{\frac {3}{2}}\right)\left(-{\frac {5}{2}}\right)}{2\cdot 3}}(-x^{2})^{3}+\cdots \\&=1+{\frac {1}{2}}x^{2}+{\frac {1\cdot 3}{2\cdot 4}}x^{4}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}x^{6}+\dots ,\end{aligned}}

d'où le résultat, en « intégrant » terme à terme.

Forme intégrale indéfinie

Cette fonction peut s'écrire sous la forme d'une intégrale indéfinie :

$\arcsin x=\int _{0}^{x}{\frac {1}{\sqrt {1-t^{2}}}}\,\mathrm {d} t$ .

Primitives

Les primitives de l'arc sinus s'obtiennent par intégration par parties :

$\int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}+C$ .

Relation entre arc sinus et arc cosinus

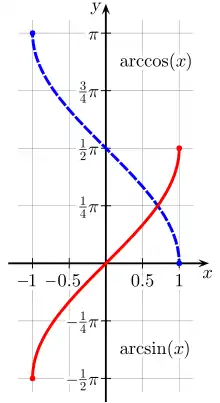
arccos(x) (bleu) et arcsin(x) (rouge)

Pour tout réel $x$ entre $-1$ et $1$ : $\arccos x+\arcsin x={\frac {\pi }{2}}$ .

Extension aux complexes

De la relation valable pour tout $z$ complexe : $sin z = -i sinh(i z)$ , on déduit

\arcsin z=-{\rm {i}}\operatorname {arsinh} ({\rm {i}}z)

D'où l'expression de la fonction arc sinus avec un logarithme complexe : $\arcsin z=-{\rm {i}}\ln \left({\rm {i}}z+{\sqrt {1-z^{2}}}\right)$ , valable pour $z\in {\mathbb {C}}\setminus ]-\infty ,-1[\cup ]1,+\infty [$ .

Le développement en série

\arcsin z=\sum _{n=0}^{\infty }{\binom {2n}{n}}{\frac {z^{2n+1}}{4^{n}(2n+1)}}

est alors valable pour tout $z$ dans le disque fermé de centre 0 et de rayon 1.

Référence

Notation issue du programme de mathématiques en CPGE, p. 10.

Voir aussi

Sinus hyperbolique réciproque

Intégrale de Wallis (pour le développement de ${\frac {\arcsin x}{\sqrt {1-x^{2}}}}$ )

(en) Eric W. Weisstein, « Inverse Sine », sur MathWorld
(en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne), § 4.4, p. 79-83

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.