Fonction circulaire réciproque

Les fonctions circulaires réciproques, ou fonctions trigonométriques inverses, sont les fonctions réciproques des fonctions circulaires, pour des intervalles de définition précis. Les fonctions réciproques des fonctions sinus, cosinus, tangente, cotangente, sécante et cosécante sont appelées arc sinus[alpha 1], arc cosinus, arc tangente, arc cotangente, arc sécante et arc cosécante.

Les fonctions circulaires réciproques servent à obtenir un angle à partir de l'une quelconque de ses lignes trigonométriques, mais aussi à expliciter les primitives de certaines fonctions. Elles sont largement utilisées dans l'ingénierie, la navigation, la physique et la géométrie.

Noms et symboles

Les noms des fonctions circulaires réciproques sont formés en faisant précéder du mot arc le nom de la fonction circulaire correspondante : arc sinus pour le sinus, arc cosinus pour le cosinus, etc.

Pour noter les fonctions circulaires réciproques on utilise différents symboles :

l'usage le plus répandu est de prendre le symbole de la fonction circulaire et de le faire précéder du préfixe arc- : arcsin(x) pour l'arc sinus de x, arccos(x) pour son arc cosinus, etc. Sauf mention spéciale ces symboles représentent les valeurs principales (cf. infra) ;
- dans les langages informatiques ces symboles sont souvent raccourcis en asin, acos, etc. (ou arsin, arcos, etc.) ;
un autre usage consiste à mettre une majuscule initiale au nom de la fonction quand il s'agissait de la valeur principale, et de considérer le symbole sans majuscule comme représentant la fonction réciproque multivaluée. Selon cette notation, $Arcsin(x)$ par exemple est l'angle compris entre $- π / 2$ et $+ π / 2$ dont le sinus vaut $x$ , alors que $arcsin(x)$ représente n'importe quel angle dont le sinus vaut $x$ ;
les textes en anglais[1] utilisent souvent les symboles $sin -1$ , $cos -1$ , etc. Cette notation, introduite par John Herschel en 1813[2], est cohérente avec la composition des fonctions (la fonction réciproque d'une fonction $f$ est souvent appelée inverse de $f$ et notée $f -1$ ), mais elle ne l'est pas avec l'usage d'écrire $sin 2 (x)$ et $sin 3 (x)$ pour signifier $[sin(x)] 2$ et $[sin(x)] 3$ : on risque de confondre $sin -1 (x)$ avec $[sin(x)] -1$ c'est-à-dire $1 / sin(x)$ .

Propriétés fondamentales

Valeurs principales

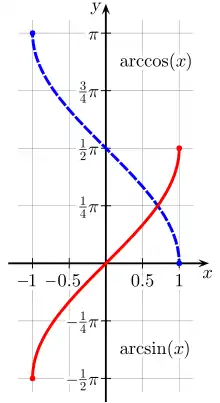
Les fonctions circulaires n'étant pas injectives, leurs fonctions réciproques sont a priori multivaluées. Pour définir univoquement ces fonctions réciproques on doit restreindre chaque fonction circulaire à un intervalle sur lequel elle est bijective (branche principale). La fonction réciproque correspondante est appelée valeur principale.

Nom	Notation usuelle	Définition	Domaine de définition	Domaine image (radians)	Domaine image (degrés)
arc sinus	$y = arcsin(x)$	$x = sin (y)$	−1 ≤ $x$ ≤ 1	− $π / 2$ ≤ $y$ ≤ $π / 2$	−90° ≤ $y$ ≤ 90°
arc cosinus	$y = arccos(x)$	$x = cos (y)$	−1 ≤ $x$ ≤ 1	0 ≤ $y$ ≤ $π$	0 ≤ $y$ ≤ 180°
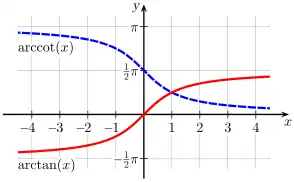
arc tangente	$y = arctan(x)$	$x = tan (y)$	tous les nombres réels	− $π / 2$ < $y$ < $π / 2$	−90° < $y$ < 90°
arc cotangente	$y = arccot(x)$	$x = cot (y)$	tous les nombres réels	0 < $y$ < $π$	0 < $y$ < 180°
arc sécante	$y = arcsec(x)$	$x = sec (y)$	$x$ ≤ −1 ou $x$ ≥ 1	0 ≤ $y$ < $π / 2$ ou $π / 2$ < $y$ ≤ $π$ [alpha 2]	0 ≤ $y$ < 90° ou 90° < $y$ ≤ 180°
arc cosécante	$y = arccsc(x)$	$x = csc (y)$	$x$ ≤ −1 ou $x$ ≥ 1	− $π / 2$ ≤ $y$ < 0 ou 0 < $y$ ≤ $π / 2$ [alpha 2]	−90° ≤ $y$ < 0 ou 0 < $y$ ≤ 90°

Si $x$ est un nombre complexe (cf. infra), alors le domaine image indiqué ci-dessus ne s'applique qu'à la partie réelle de $y$ .

Fonctions réciproques multivaluées

Dans les formules ci-dessous, $k$ désigne un entier quelconque.

$x=\sin(y)\;\Leftrightarrow \;y=\arcsin(x)+2\pi k\;{\text{ ou }}\;y=\pi -\arcsin(x)+2\pi k$
ou, en une seule formule : $x=\sin(y)\;\Leftrightarrow \;y=(-1)^{k}\arcsin(x)+\pi k$
$x=\cos(y)\;\Leftrightarrow \;y=\arccos(x)+2\pi k\;{\text{ ou }}\;y=2\pi -\arccos(x)+2\pi k$
ou, en une seule formule : $x=\cos(y)\;\Leftrightarrow \;y=\pm \arccos(x)+2\pi k$
$x=\tan(y)\;\Leftrightarrow \;y=\arctan(x)+\pi k$
$x=\cot(y)\;\Leftrightarrow \;y=\operatorname {arccot}(x)+\pi k$
$x=\sec(y)\;\Leftrightarrow \;y=\operatorname {arcsec}(x)+2\pi k{\text{ ou }}y=2\pi -\operatorname {arcsec}(x)+2\pi k$
ou, en une seule formule : $x=\sec(y)\;\Leftrightarrow \;y=\pm \operatorname {arcsec}(x)+2\pi k$
$x=\csc(y)\;\Leftrightarrow \;y=\operatorname {arccsc}(x)+2\pi k{\text{ ou }}y=\pi -\operatorname {arccsc}(x)+2\pi k$
ou, en une seule formule : $x=\csc(y)\;\Leftrightarrow \;y=(-1)^{k}\operatorname {arccsc}(x)+\pi k$

Démonstration

Chacune des fonctions sinus, cosinus, sécante et cosécante est périodique de période $2π$ et prend deux fois chaque valeur sur une même période. Chacune des fonctions tangente et cotangente est périodique de période $π$ et prend une fois chaque valeur sur une même période.

Le sinus est bijectif sur l'intervalle $\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$ , donc sur cet intervalle $x=\sin(y)\Rightarrow y=\arcsin(x)$ . Il est symétrique par rapport à l'argument $π / 2$ (c'est-à-dire, $sin(π- y) = sin(y)$ ), donc sur l'intervalle $\left[{\frac {\pi }{2}},{\frac {3\pi }{2}}\right]$ $x=\sin(y)\Rightarrow y=\pi -\arcsin(x)$ . En regroupant ces deux résultats on voit que sur l'intervalle $\left[-{\frac {\pi }{2}},{\frac {3\pi }{2}}\right]$ $x=\sin(y)\Rightarrow y=\arcsin(x)\;{\text{ ou }}\;y=\pi -\arcsin(x)$ . Le sinus est périodique de période $2π$ , donc finalement $x=\sin(y)\Rightarrow y=\arcsin(x)+2\pi k\;{\text{ ou }}\;y=\pi -\arcsin(x)+2\pi k$ .
Le cosinus est bijectif sur l'intervalle $[0 ; π]$ , donc sur cet intervalle $x=\cos(y)\Rightarrow y=\arccos(x)$ . Il est symétrique par rapport à l'argument $π$ (c'est-à-dire, $\cos(2\pi -y)=\cos(y)$ ), donc sur l'intervalle $\left[\pi ,2\pi \right]$ $x=\cos(y)\Rightarrow y=2\pi -\arccos(x)$ . En regroupant ces deux résultats on voit que sur l'intervalle $[0 ; 2π]$ $x=\cos(y)\Rightarrow y=\arccos(x)\;{\text{ ou }}\;y=2\pi -\arccos(x)$ . Le cosinus est périodique de période $2π$ , donc finalement $x=\cos(y)\Rightarrow y=\arccos(x)+2\pi k\;{\text{ ou }}\;y=2\pi -\arccos(x)+2\pi k$ .
Pour la sécante, le raisonnement est le même que pour le cosinus.
Pour la cosécante, le raisonnement est le même que pour le sinus.
La tangente est bijective sur l'intervalle $\left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[$ , donc sur cet intervalle $x=\tan(y)\Rightarrow y=\arctan(x)$ . Elle est périodique de période $π$ , donc finalement $x=\tan(y)\;\Rightarrow \;y=\arctan(x)+\pi k$ .
Pour la cotangente, le raisonnement est le même que pour la tangente.

Relations entre fonctions circulaires et fonctions circulaires réciproques

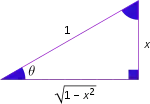
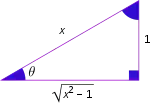
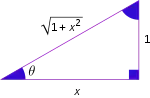
Le tableau ci-dessous indique le résultat des fonctions circulaires appliquées aux fonctions circulaires réciproques. On retrouve facilement ces valeurs en considérant un triangle rectangle dont un côté a la longueur $x$ (n'importe quel nombre réel compris entre 0 et 1) et l'autre est de longueur unité[alpha 3].

$\theta$	$\sin(\theta )$	$\cos(\theta )$	$\tan(\theta )$
$\arcsin(x)$	$\sin[\arcsin(x)]=x$	$\cos[\arcsin(x)]={\sqrt {1-x^{2}}}$	$\tan[\arcsin(x)]={\frac {x}{\sqrt {1-x^{2}}}}$
$\arccos(x)$	$\sin[\arccos(x)]={\sqrt {1-x^{2}}}$	$\cos[\arccos(x)]=x$	$\tan[\arccos(x)]={\frac {\sqrt {1-x^{2}}}{x}}$
$\arctan(x)$	$\sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}$	$\cos[\arctan(x)]={\frac {1}{\sqrt {1+x^{2}}}}$	$\tan[\arctan(x)]=x$
$\operatorname {arccsc}(x)$	$\sin[\operatorname {arccsc}(x)]={\frac {1}{x}}$	$\cos[\operatorname {arccsc}(x)]={\frac {\sqrt {x^{2}-1}}{x}}$	$\tan[\operatorname {arccsc}(x)]={\frac {1}{\sqrt {x^{2}-1}}}$
$\operatorname {arcsec}(x)$	$\sin[\operatorname {arcsec}(x)]={\frac {\sqrt {x^{2}-1}}{x}}$	$\cos[\operatorname {arcsec}(x)]={\frac {1}{x}}$	$\tan[\operatorname {arcsec}(x)]={\sqrt {x^{2}-1}}$
$\operatorname {arccot}(x)$	$\sin[\operatorname {arccot}(x)]={\frac {1}{\sqrt {1+x^{2}}}}$	$\cos[\operatorname {arccot}(x)]={\frac {x}{\sqrt {1+x^{2}}}}$	$\tan[\operatorname {arccot}(x)]={\frac {1}{x}}$

Relations des fonctions circulaires réciproques entre elles

Graphe cartésien des valeurs principales d'

arcsin(x)

(en rouge) et d'

arccos(x)

(en bleu), en fonction de

x

Graphe cartésien des valeurs principales d'

arctan(x)

(en rouge) et d'

arccot(x)

(en bleu), en fonction de

x

Graphe cartésien des valeurs principales d'

arcsec(x)

(en rouge) et d'

arccsc(x)

(en bleu), en fonction de

x

Angles complémentaires

{\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}

Arguments opposés

{\begin{aligned}\arcsin(-x)&=-\arcsin(x)\\\arccos(-x)&=\pi -\arccos(x)\\\arctan(-x)&=-\arctan(x)\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccot}(x)\\\operatorname {arcsec}(-x)&=\pi -\operatorname {arcsec}(x)\\\operatorname {arccsc}(-x)&=-\operatorname {arccsc}(x)\end{aligned}}

Arguments inverses

{\begin{aligned}\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)\\[0.3em]\arctan \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)\,,{\text{ si }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=-{\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)-\pi \,,{\text{ si }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\operatorname {arccot}(x)=\arctan(x)\,,{\text{ si }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {3\pi }{2}}-\operatorname {arccot}(x)=\pi +\arctan(x)\,,{\text{ si }}x<0\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)\end{aligned}}

Autres formules

Les formules ci-dessous sont utiles, soit quand on dispose d'une table incomplète (par exemple, pour la première, quand la table ne liste que des arguments inférieurs à ½), soit pour simplifier des formules obtenues lors d'un calcul de primitives (quand on rencontre l'un des seconds membres indiqués).

{\begin{aligned}\arccos(x)&=\arcsin \left({\sqrt {1-x^{2}}}\right)\,,{\text{ si }}0\leq x\leq 1\\\arccos(x)&={\frac {1}{2}}\arccos \left(2x^{2}-1\right)\,,{\text{ si }}0\leq x\leq 1\\\arcsin(x)&={\frac {1}{2}}\arccos \left(1-2x^{2}\right)\,,{\text{ si }}0\leq x\leq 1\\\arctan(x)&=\arcsin \left({\frac {x}{\sqrt {x^{2}+1}}}\right)\end{aligned}}

Quand l'une de ces formules fait intervenir la racine carrée d'un nombre complexe (ou d'un nombre réel négatif), la racine choisie est celle qui a une partie réelle positive (ou une partie imaginaire positive).

Formules déduites de la tangente de l'arc moitié

{\begin{aligned}\arcsin(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)\\[0.5em]\arccos(x)&=2\arctan \left({\frac {\sqrt {1-x^{2}}}{1+x}}\right)\,,{\text{ si }}-1<x\leq +1\\[0.5em]\arctan(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1+x^{2}}}}}\right)\end{aligned}}

Démonstrations

La formule de la « tangente de l'arc moitié » est :

\tan \left({\frac {\theta }{2}}\right)={\frac {\sin(\theta )}{1+\cos(\theta )}}

On peut l'écrire :

\tan \left({\frac {\theta }{2}}\right)={\frac {\sin(\theta )}{1+{\sqrt {1-\sin ^{2}(\theta )}}}}={\frac {\sqrt {1-\cos ^{2}(\theta )}}{1+\cos(\theta )}}={\frac {\tan(\theta )}{1+{\sqrt {1+\tan ^{2}(\theta )}}}}

ou :

\theta =2\arctan \left[{\frac {\sin(\theta )}{1+{\sqrt {1-\sin ^{2}(\theta )}}}}\right]=2\arctan \left[{\frac {\sqrt {1-\cos ^{2}(\theta )}}{1+\cos(\theta )}}\right]=2\arctan \left[{\frac {\tan(\theta )}{1+{\sqrt {1+\tan ^{2}(\theta )}}}}\right]

On obtient bien les formules indiquées en posant, soit $x = sin(θ)$ , soit $x = cos(θ)$ , soit $x = tan(θ)$ (alors $θ$ égale, soit $arcsin(x)$ , soit $arccos(x)$ , soit $arctan(x)$ ).

Addition des arcs tangente

Si $uv\neq 1$ , alors $\arctan u+\arctan v\equiv \arctan {\frac {u+v}{1-uv}}\mod \pi$ .

Calcul

Dérivées

Les formules ci-dessous sont valables pour $z$ quelconque, réel ou complexe.

{\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\arcsin(z)&{}={\frac {1}{\sqrt {1-z^{2}}}}\;;&z&{}\neq -1,+1\\{\frac {\mathrm {d} }{\mathrm {d} z}}\arccos(z)&{}=-{\frac {1}{\sqrt {1-z^{2}}}}\;;&z&{}\neq -1,+1\\{\frac {\mathrm {d} }{\mathrm {d} z}}\arctan(z)&{}={\frac {1}{1+z^{2}}}\;;&z&{}\neq -\mathrm {i} ,+\mathrm {i} \\{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {arccot}(z)&{}=-{\frac {1}{1+z^{2}}}\;;&z&{}\neq -\mathrm {i} ,+\mathrm {i} \\{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {arcsec}(z)&{}={\frac {1}{z^{2}{\sqrt {1-{\frac {1}{z^{2}}}}}}}\;;&z&{}\neq -1,0,+1\\{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {arccsc}(z)&{}=-{\frac {1}{z^{2}{\sqrt {1-{\frac {1}{z^{2}}}}}}}\;;&z&{}\neq -1,0,+1\end{aligned}}

Démonstration

Le calcul de ces dérivées est facile à retrouver. Pour l'arc sinus par exemple, on pose $θ = arcsin(x)$ :

{\frac {\mathrm {d} \arcsin(x)}{\mathrm {d} x}}={\frac {\mathrm {d} \theta }{\mathrm {d} \sin(\theta )}}={\frac {\mathrm {d} \theta }{\cos(\theta )\mathrm {d} \theta }}={\frac {1}{\cos(\theta )}}={\frac {1}{\sqrt {1-\sin ^{2}(\theta )}}}={\frac {1}{\sqrt {1-x^{2}}}}

Les formules ci-dessous ne sont valables que pour $x$ réel.

{\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arcsec}(x)&{}={\frac {1}{|x|{\sqrt {x^{2}-1}}}}\;;&|x|>1\\{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arccsc}(x)&{}=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}\;;&|x|>1\end{aligned}}

Expression sous forme d'intégrale définie

En intégrant les dérivées ci-dessus on peut exprimer les fonctions circulaires sous la forme d'intégrales définies de fonctions algébriques :

{\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z\;,&|x|&{}\leq 1\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z\;,&|x|&{}\leq 1\\\arctan(x)&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,\mathrm {d} z\;,\\\operatorname {arccot}(x)&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,\mathrm {d} z\;,\\\operatorname {arcsec}(x)&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,\mathrm {d} z=\pi +\int _{x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,\mathrm {d} z\;,&x&{}\geq 1\\\operatorname {arccsc}(x)&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,\mathrm {d} z=\int _{-\infty }^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,\mathrm {d} z\;,&x&{}\geq 1\\\end{aligned}}

Quand $x$ = 1, les intégrales définissant $arcsin(x)$ , $arccos(x)$ , $arcsec(x)$ et $arccsc(x)$ sont impropres mais convergent correctement.

Développement en série

Comme les fonctions circulaires, les fonctions circulaires réciproques sont développables en séries entières :

\arcsin z=z+{\frac {1}{2}}\cdot {\frac {z^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {z^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {z^{7}}{7}}+\dots =\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}\cdot {\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1

\arctan z=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\qquad z\neq \mathrm {i} ,-\mathrm {i}

Pour développer en série les autres fonctions circulaires réciproques il suffit d'utiliser leurs relations (voir supra) : $arccos(x) = π / 2 - arcsin(x)$ , $arccsc(x) = arcsin(1/ x)$ , etc..

Un développement du carré de l'arc sinus est[3] :

\arcsin ^{2}(x)={\frac {1}{2}}\sum _{n=1}^{\infty }{\frac {(2x)^{2n}}{n^{2}{\binom {2n}{n}}}}

Un autre développement de l'arc tangente, plus efficace numériquement que la série entière, a été obtenu par Euler[alpha 4] :

\arctan z={\frac {z}{1+z^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2})}}

On peut donner une variante du développement précédent :

\arctan z=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n+1)!}}\;{\frac {z^{2n+1}}{(1+z^{2})^{n+1}}}

Développement en fraction continue

On connaît deux développements de l'arc tangente en fraction continue généralisée, le premier obtenu par Euler et le second par Gauss (à l'aide des fonctions hypergéométriques) :

\arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}

Le développement de Gauss est valable pour des nombres complexes, à l'exception des imaginaires purs de module supérieur ou égal à 1. Il est surtout efficace pour les nombres réels compris entre −1 et +1.

Primitives

Pour $z$ réel ou complexe :

{\begin{aligned}\int \arcsin(z)\,\mathrm {d} z&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,\mathrm {d} z&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,\mathrm {d} z&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,\mathrm {d} z&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,\mathrm {d} z&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,\mathrm {d} z&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}

Pour $x$ réel et supérieur à 1 :

{\begin{aligned}\int \operatorname {arcsec}(x)\,\mathrm {d} x&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,\mathrm {d} x&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}

Pour $x$ réel et de valeur absolue supérieure à 1 :

{\begin{aligned}\int \operatorname {arcsec}(x)\,\mathrm {d} x&{}=x\,\operatorname {arcsec}(x)-\operatorname {sgn}(x)\ln \left(\left|x+{\sqrt {x^{2}-1}}\right|\right)+C\\\int \operatorname {arccsc}(x)\,\mathrm {d} x&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left(\left|x+{\sqrt {x^{2}-1}}\right|\right)+C\end{aligned}}

Dans les expressions ci-dessus la valeur absolue (|•|) est due au signe variable de l'arc sécante et de l'arc cosécante, et la fonction signe (sgn) aux valeurs absolues des dérivées de ces deux fonctions, ce qui conduit à des expressions différentes selon le signe de $x$ . On peut simplifier ces formules en faisant appel aux fonctions hyperboliques réciproques :

{\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {arcosh} (|x|)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {arcosh} (|x|)+C\\\end{aligned}}

Démonstrations

On obtient les primitives ci-dessus par la méthode d'intégration par parties $\int u\,\mathrm {d} v=uv-\int v\,\mathrm {d} u$ . Par exemple pour l'arc sinus :

{\begin{aligned}u&=\arcsin(x)&\mathrm {d} v&=\mathrm {d} x\\\mathrm {d} u&={\frac {\mathrm {d} x}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}}

Alors :

\int \arcsin(x)\,\mathrm {d} x=x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x,

ce qui donne, par le changement de variable $t = 1 - x 2$ :

\int \arcsin(x)\,\mathrm {d} x=x\arcsin(x)+{\sqrt {1-x^{2}}}+C

Extension au plan complexe

Étant développables en série entière, les fonctions circulaires réciproques sont analytiques, c'est-à-dire que leur ensemble de définition (la droite des nombres réels) peut être étendu au plan complexe. Ces fonctions étant fondamentalement multivaluées, leurs extensions au plan complexe ont de multiples feuillets et points de branchement.

On peut ainsi définir l'arc tangente par :

\arctan(z)=\int _{0}^{z}{\frac {\mathrm {d} x}{1+x^{2}}}\quad z\neq -\mathrm {i} ,+\mathrm {i}

La coupure entre le feuillet principal et les autres feuillets est constituée par les deux demi-droites portant les imaginaires purs de module supérieur ou égal à 1.

On définit les autres fonctions circulaires réciproques à l'aide des relations entre ces fonctions :

\arcsin(z)=\arctan \left({\frac {z}{\sqrt {1-z^{2}}}}\right)\quad z\neq -1,+1

\arccos(z)={\frac {\pi }{2}}-\arcsin(z)\quad z\neq -1,+1

\operatorname {arccot}(z)={\frac {\pi }{2}}-\arctan(z)\quad z\neq -\mathrm {i} ,\mathrm {i}

\operatorname {arcsec}(z)=\arccos \left({\frac {1}{z}}\right)\quad z\neq -1,0,+1

\operatorname {arccsc}(z)=\arcsin \left({\frac {1}{z}}\right)\quad z\neq -1,0,+1

La coupure de l'arc sinus est constituée par les deux demi-droites portant les réels de valeur absolue supérieure ou égale à 1. L'arc cosinus a la même coupure que l'arc sinus, et l'arc cotangente la même que l'arc tangente. L'arc sécante et l'arc cosécante ont pour coupure le segment réel $[-1 ; +1]$ .

Formes logarithmiques

Les fonctions circulaires réciproques peuvent être exprimées sous la forme de logarithmes complexes :

{\begin{aligned}\arcsin(z)&{}=-\mathrm {i} \ln \left(\mathrm {i} z+{\sqrt {1-z^{2}}}\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-\mathrm {i} \ln \left(z+\mathrm {i} {\sqrt {z^{2}-1}}\right)={\frac {\pi }{2}}\,+\mathrm {i} \ln \left(\mathrm {i} z+{\sqrt {1-z^{2}}}\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}={\frac {1}{2}}\mathrm {i} \left[\ln \left(1-\mathrm {i} z\right)-\ln \left(1+\mathrm {i} z\right)\right]&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}={\frac {1}{2}}\mathrm {i} \left[\ln \left(1-{\frac {\mathrm {i} }{z}}\right)-\ln \left(1+{\frac {\mathrm {i} }{z}}\right)\right]&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-\mathrm {i} \ln \left({\sqrt {{\frac {1}{z^{2}}}-1}}+{\frac {1}{z}}\right)=\mathrm {i} \,\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-\mathrm {i} \ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {\mathrm {i} }{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}

Démonstrations

On obtient ces expressions logarithmiques à partir de la forme exponentielle des fonctions circulaires. Par exemple pour l'arc sinus :

\sin(\phi )=z

\phi =\arcsin(z)

En exprimant le sinus en termes d'exponentielles complexes :

z={\frac {\mathrm {e} ^{\mathrm {i} \phi }-\mathrm {e} ^{-\mathrm {i} \phi }}{2\mathrm {i} }}

Soit :

\xi =\mathrm {e} ^{\mathrm {i} \phi }

On en extrait $ϕ$ , qu'on reporte dans l'expression de $z$ :

z={\frac {\xi -{\frac {1}{\xi }}}{2\mathrm {i} }}

2\mathrm {i} z={\xi -{\frac {1}{\xi }}}

{\xi -2\mathrm {i} z-{\frac {1}{\xi }}}=0

\xi ^{2}-2\mathrm {i} \xi z-1\,=\,0

\xi =\mathrm {i} z\pm {\sqrt {1-z^{2}}}=\mathrm {e} ^{\mathrm {i} \phi }

\mathrm {i} \phi =\ln \left(\mathrm {i} z\pm {\sqrt {1-z^{2}}}\right)

\phi =-\mathrm {i} \ln \left(\mathrm {i} z\pm {\sqrt {1-z^{2}}}\right)

(on a choisi la branche positive)

\phi =\arcsin(z)=-\mathrm {i} \ln \left(\mathrm {i} z+{\sqrt {1-z^{2}}}\right)

Représentation des fonctions circulaires réciproques par coloration de régions dans le plan complexe

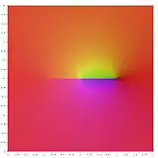$arcsin(z)$	$arccos(z)$	$arctan(z)$	$arccot(z)$	$arcsec(z)$	$arccsc(z)$

Applications

Triangle rectangle

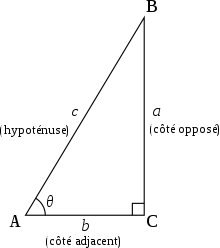
Triangle trigonométrique : relations entre un angle et les côtés du triangle.

Les fonctions circulaires réciproques permettent d'exprimer un angle d'un triangle rectangle en fonction de deux des côtés :

{\begin{aligned}\theta &=\arcsin \left({\frac {\text{côté opposé}}{\text{hypoténuse}}}\right)=\arccos \left({\frac {\text{côté adjacent}}{\text{hypoténuse}}}\right)\\&=\arctan \left({\frac {\text{côté opposé}}{\text{côté adjacent}}}\right)=\operatorname {arccot} \left({\frac {\text{côté adjacent}}{\text{côté opposé}}}\right)\\&=\operatorname {arcsec} \left({\frac {\text{hypoténuse}}{\text{côté adjacent}}}\right)=\operatorname {arccsc} \left({\frac {\text{hypoténuse}}{\text{côté opposé}}}\right)\end{aligned}}

ou, avec les notations de la figure ci-contre :

\theta =\arcsin \left({\frac {a}{c}}\right)=\arccos \left({\frac {b}{c}}\right)=\arctan \left({\frac {a}{b}}\right)=\operatorname {arccot} \left({\frac {b}{a}}\right)=\operatorname {arcsec} \left({\frac {c}{b}}\right)=\operatorname {arccsc} \left({\frac {c}{a}}\right)

Arc tangente à deux arguments

L'arc tangente à deux arguments, de symbole usuel atan2, est une variante de l'arc tangente initialement introduite dans les langages informatiques (Fortran, notamment). Pour $x$ et $y$ réels et non tous les deux nuls, $atan2(y, x)$ est, dans un repère orthonormé, l'angle polaire du point d'abscisse $x$ et d'ordonnée $y$ . Autrement dit, c'est l'argument du nombre complexe $x + i y$ . L'intérêt de cette fonction est double :

le domaine image d'atan2 est $[-π , π]$ alors que celui de l'arc tangente est $[-π/2 , π/2]$ : $atan2(- y,- x)$ et $atan2(y, x)$ diffèrent de $π$ alors que $\arctan \left({\tfrac {-y}{-x}}\right)=\arctan \left({\tfrac {y}{x}}\right)$ . Plus généralement, atan2 donne l'angle polaire en un seul calcul alors qu'aucune des fonctions circulaires réciproques ne le fait ;
quand $x = 0$ la fonction atan2 prend la valeur $π / 2$ ou – $π / 2$ (selon le signe de $y$ ) alors que la plupart des langages informatiques ne permettent pas de coder un argument infini. Plus généralement, $atan2(y, x)$ se comporte bien numériquement quand $| x | << | y |$ alors que ce n'est pas le cas de $arctan(y / x)$ .

Primitive d'une fonction rationnelle

Pour intégrer une fonction rationnelle $R (x)$ (où $x$ est une variable réelle) on la décompose en éléments simples :

R(x)=T+F_{1}+\ldots +F_{p}+G_{1}+\ldots +G_{q}\quad {\rm {et}}\quad {\begin{cases}T&{\text{est un polynôme de }}x\\F_{i}&={\frac {a_{i,1}}{x-z_{i}}}+{\frac {a_{i,2}}{(x-z_{i})^{2}}}+\ldots +{\frac {a_{i,n_{i}}}{(x-z_{i})^{n_{i}}}}\\G_{j}&={\frac {b_{j,1}x+c_{j,1}}{x^{2}-\beta _{j}x+\gamma _{j}}}+{\frac {b_{j,2}x+c_{j,2}}{(x^{2}-\beta _{j}x+\gamma _{j})^{2}}}+\ldots +{\frac {b_{j,m_{j}}x+c_{j,m_{j}}}{(x^{2}-\beta _{j}x+\gamma _{j})^{m_{j}}}}\end{cases}}

où les trinômes $x 2 - β j x + γ j$ n'ont pas de racines réelles (discriminant négatif : $Δ = β j 2 - 4 γ j < 0$ ). Ensuite :

le terme $T$ (partie entière) s'intègre directement en donnant un autre polynôme ;
les termes $F i$ (éléments simples de première espèce) s'intègrent directement (le résultat mêle fonctions rationnelles et logarithmes) ;
par un changement de variable simple (linéaire) x → u, chaque terme de seconde espèce ${\frac {b_{j,m}x+c_{j,m}}{(x^{2}-\beta _{j}x+\gamma _{j})^{m}}}$ ${\frac {b_{j,m}x+c_{j,m}}{(x^{2}-\beta _{j}x+\gamma _{j})^{m}}}$ se ramène à l'intégration de ${\frac {u}{(u^{2}+1)^{m}}}$ ${\frac {u}{(u^{2}+1)^{m}}}$ et/ou de ${\frac {1}{(u^{2}+1)^{m}}}$ ${\frac {1}{(u^{2}+1)^{m}}}$ :
- ${\frac {u}{(u^{2}+1)^{m}}}$ s'intègre directement (le résultat est une fonction rationnelle ou un logarithme),
- l'intégration de ${\frac {1}{(u^{2}+1)^{m}}}$ implique l'arc tangente :
  $\int {\frac {1}{u^{2}+1}}\mathrm {d} u=\arctan(u)+C$ ,
  
  $\int {\frac {1}{(u^{2}+1)^{2}}}\mathrm {d} u={\frac {1}{2}}\left[{\frac {u}{u^{2}+1}}+\arctan(u)\right]+C$ ,
  
  $\int {\frac {1}{(u^{2}+1)^{3}}}\mathrm {d} u={\frac {1}{8}}\left[{\frac {u(3u^{2}+5)}{(u^{2}+1)^{2}}}+3\arctan(u)\right]+C$ , etc.

Primitive d'une fonction où interviennent des radicaux

Pour intégrer une fonction comportant le radical $\sqrt 1 - x 2$ , l'une des pistes consiste à prendre pour nouvelle variable $θ = arcsin(x)$ :
$x = sin(θ)$ , donc ${\sqrt {1-x^{2}}}=\cos(\theta )$ et $\mathrm {d} x=\cos(\theta )\,\mathrm {d} \theta$ : le radical a disparu.
Pour intégrer une fonction comportant le radical $\sqrt 1 + x 2$ , l'une des pistes consiste à prendre pour nouvelle variable $θ = arctan(x)$ :
$x = tan(θ)$ , donc ${\sqrt {1+x^{2}}}={\frac {1}{\cos(\theta )}}$ et $\mathrm {d} x={\frac {\mathrm {d} \theta }{\cos ^{2}(\theta )\,}}$ : le radical a disparu.

Plus généralement :

pour se débarrasser du radical ${\sqrt {a^{2}-b^{2}x^{2}}}$ on peut poser $\theta =\arcsin \left({\frac {b}{a}}x\right)$ ;
pour se débarrasser du radical ${\sqrt {a^{2}+b^{2}x^{2}}}$ on peut poser $\theta =\arctan \left({\frac {b}{a}}x\right)$ .

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Inverse trigonometric functions » (voir la liste des auteurs).

Notes

La logique de cette dénomination est la suivante : l'arc sinus de x est l'arc (l'angle) dont le sinus est x.
Certains auteurs définissent le domaine image de l'arc sécante comme (0 ≤ $y$ < $π / 2$ ou $π$ ≤ $y$ < $3π / 2$ ), parce que la fonction tangente est non-négative dans ce domaine. Cette définition rend certains calculs plus cohérents. On obtient par exemple $tan(arcsec(x)) = \sqrt x 2 - 1$ , alors qu'avec le domaine image (0 ≤ $y$ < $π / 2$ ou $π / 2$ < $y$ ≤ $π$ ) on doit écrire $tan(arcsec(x)) = \pm \sqrt x 2 - 1$ , vu que la tangente est non-négative sur 0 ≤ $y$ < $π / 2$ mais non-positive sur $π / 2$ < $y$ ≤ $π$ . Pour la même raison, ces mêmes auteurs définissent le domaine image de l'arc cosécante comme − $π$ < $y$ ≤ − $π / 2$ ou 0 < $y$ ≤ $π / 2$ .
On retrouve aussi ces résultats par un calcul algébrique, mais c'est plus long.
Pour $n = 0$ le produit Π est vide et vaut donc 1, par définition.

Références

(en) Arthur Graham Hall et Fred Goodrich Frink, chap. II « The Acute Angle [14] Inverse trigonometric functions », dans Trigonometry, Ann Arbor, Michigan, USA, Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA, janvier 1909 (lire en ligne), I: Plane Trigonometry, p. 15.
(en) John Frederick William Herschel, « On a remarkable Application of Cotes's Theorem », Philosophical Transactions, Londres, Royal Society, vol. 103, n^o 1,‎ 1813, p. 8 (lire en ligne).
Voir (en) Jonathan Borwein, David Bailey et Roland Gingersohn, Experimentation in Mathematics : Computational Paths to Discovery, Wellesley, MA, A K Peters, 2004, 368 p. (ISBN 978-1-4398-6419-7, lire en ligne), p. 51 (exercice 16, sur la formule de Clausen (en)) ou, plus simplement, cet exercice corrigé sur Wikiversité.

Voir aussi

Lien externe

(en) Eric W. Weisstein, « Inverse Trigonometric Functions », sur MathWorld

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

Fonction circulaire réciproque

Noms et symboles

Propriétés fondamentales

Valeurs principales

Fonctions réciproques multivaluées

Relations entre fonctions circulaires et fonctions circulaires réciproques

Relations des fonctions circulaires réciproques entre elles

Angles complémentaires

Arguments opposés

Arguments inverses

Autres formules

Formules déduites de la tangente de l'arc moitié

Addition des arcs tangente

Calcul

Dérivées

Expression sous forme d'intégrale définie

Développement en série

Développement en fraction continue

Primitives

Extension au plan complexe

Formes logarithmiques

Applications

Triangle rectangle

Arc tangente à deux arguments

Primitive d'une fonction rationnelle

Primitive d'une fonction où interviennent des radicaux

Notes et références

Notes

Références

Voir aussi

Articles connexes

Lien externe