Identité trigonométrique

Une identité trigonométrique est une relation impliquant des fonctions trigonométriques, vérifiée pour toutes les valeurs possibles des variables intervenant dans la relation. Ces identités peuvent servir à simplifier une expression comportant des fonctions trigonométriques ou à la transformer (par exemple pour en calculer une primitive). Elles constituent donc une « boîte à outils » utile pour la résolution de problèmes.

Les fonctions trigonométriques sont définies géométriquement ou analytiquement. Elles servent beaucoup en intégration, pour intégrer des fonctions « non trigonométriques » : un procédé habituel consiste à effectuer un changement de variable en utilisant une fonction trigonométrique, et à simplifier ensuite l'intégrale obtenue avec les identités trigonométriques.

Notation : si $ƒ$ est une fonction trigonométrique, $ƒ 2$ désigne la fonction qui à tout réel $x$ associe le carré de $ƒ(x)$ . Par exemple : $cos 2 x = (cos x) 2$ .

Relations entre fonctions trigonométriques

Les relations entre fonctions trigonométriques résultent d'une part des définitions

\tan \theta ={\frac {\sin \theta }{\cos \theta }},\quad \cot \theta ={\frac {\cos \theta }{\sin \theta }},\quad \ldots

et d'autre part de l'application du théorème de Pythagore, notamment :

\cos ^{2}\theta +\sin ^{2}\theta =1\quad \tan ^{2}\theta +1={\frac {1}{\cos ^{2}\theta }},\quad \cot ^{2}\theta +1={\frac {1}{\sin ^{2}\theta }}.

Relations entre fonctions trigonométriques dans le premier quadrant ( $0\leqslant \theta \leqslant {\tfrac {\pi }{2}}$ )[1], éventuellement non valables en 0 ou ${\frac {\pi }{2}}$
	cos	sin	tan	cot	sec	csc
cos		$\cos \theta ={\sqrt {1-\sin ^{2}\theta }}$	$\cos \theta ={\frac {1}{\sqrt {1+\tan ^{2}\theta }}}$	$\cos \theta ={\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}$	$\cos \theta ={\frac {1}{\sec \theta }}$	$\cos \theta ={\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}$
sin	$\sin \theta ={\sqrt {1-\cos ^{2}\theta }}$		$\sin \theta ={\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}$	$\sin \theta ={\frac {1}{\sqrt {1+\cot ^{2}\theta }}}$	$\sin \theta ={\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}$	$\sin \theta ={\frac {1}{\csc \theta }}$
tan	$\tan \theta ={\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}$	$\tan \theta ={\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}$		$\tan \theta ={\frac {1}{\cot \theta }}$	$\tan \theta ={\sqrt {\sec ^{2}\theta -1}}$	$\tan \theta ={\frac {1}{\sqrt {\csc ^{2}\theta -1}}}$
cot	$\cot \theta ={\frac {\cos \theta }{\sqrt {1-\cos ^{2}\theta }}}$	$\cot \theta ={\frac {\sqrt {1-\sin ^{2}\theta }}{\sin \theta }}$	$\cot \theta ={\frac {1}{\tan \theta }}$		$\cot \theta ={\frac {1}{\sqrt {\sec ^{2}\theta -1}}}$	$\cot \theta ={\sqrt {\csc ^{2}\theta -1}}$
sec	$\sec \theta ={\frac {1}{\cos \theta }}$	$\sec \theta ={\frac {1}{\sqrt {1-\sin ^{2}\theta }}}$	$\sec \theta ={\sqrt {1+\tan ^{2}\theta }}$	$\sec \theta ={\frac {\sqrt {1+\cot ^{2}\theta }}{\cot \theta }}$		$\sec \theta ={\frac {\csc \theta }{\sqrt {\csc ^{2}\theta -1}}}$
csc	$\csc \theta ={\frac {1}{\sqrt {1-\cos ^{2}\theta }}}$	$\csc \theta ={\frac {1}{\sin \theta }}$	$\csc \theta ={\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}$	$\csc \theta ={\sqrt {1+\cot ^{2}\theta }}$	$\csc \theta ={\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}$

Propriétés liées au cercle trigonométrique

Symétries, parité

Parité - Réflexion d'axe ( $θ = 0$ )	Réflexion d'axe ( $θ = π/4$ )	Réflexion d'axe ( $θ = π/2$ )
${\begin{aligned}\sin(-\theta )&=-\sin \theta \\\cos(-\theta )&=+\cos \theta \\\tan(-\theta )&=-\tan \theta \\\cot(-\theta )&=-\cot \theta \end{aligned}}$	${\begin{aligned}\sin({\tfrac {\pi }{2}}-\theta )&=+\cos \theta \\\cos({\tfrac {\pi }{2}}-\theta )&=+\sin \theta \\\tan({\tfrac {\pi }{2}}-\theta )&=+\cot \theta \\\cot({\tfrac {\pi }{2}}-\theta )&=+\tan \theta \end{aligned}}$	${\begin{aligned}\sin(\pi -\theta )&=+\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \\\cot(\pi -\theta )&=-\cot \theta \\\end{aligned}}$

Note : Toutes ces formules sont également utilisables pour des ajouts d'angles, il suffit pour cela de prendre l'opposé : par exemple, $\sin({\tfrac {\pi }{2}}+\theta )=\sin({\tfrac {\pi }{2}}-(-\theta ))=\cos(-\theta )$ . Il suffit ensuite d'appliquer la formule de simplification correspondante de la première colonne.

Périodicité, décalages

Décalage de $π/2$	Décalage de $π$ (Période de tan et cot)	Décalage de $2π$ (Période de sin et cos)
${\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})&=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})&=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})&=-\cot \theta \\\cot(\theta +{\tfrac {\pi }{2}})&=-\tan \theta \end{aligned}}$	${\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=+\tan \theta \\\cot(\theta +\pi )&=+\cot \theta \\\end{aligned}}$	${\begin{aligned}\sin(\theta +2\pi )&=+\sin \theta \\\cos(\theta +2\pi )&=+\cos \theta \\\tan(\theta +2\pi )&=+\tan \theta \\\cot(\theta +2\pi )&=+\cot \theta \end{aligned}}$

Équations trigonométriques

Certaines des relations ci-dessus sont renforcées par les équivalences suivantes[2] :

\cos a=\cos b\Leftrightarrow a=b+2k\pi \quad {\text{ou}}\quad a=-b+2k\pi \qquad (k\in \mathbb {Z} )

\sin a=\sin b\Leftrightarrow a=b+2k\pi \quad {\text{ou}}\quad a=\pi -b+2k\pi \qquad (k\in \mathbb {Z} )

\tan a=\tan b\Leftrightarrow a=b+k\pi \qquad (k\in \mathbb {Z} )

Formules d'addition et de différence

Les deux formules principales sont les formules d'addition pour le cosinus et le sinus[3] - [4] :

\cos(a+b)=\cos a\cos b-\sin a\sin b

\sin(a+b)=\sin a\cos b+\cos a\sin b

En remplaçant $b$ par son opposé, on obtient aussi les formules de différence[4] :

\cos(a-b)=\cos a\cos b+\sin a\sin b

\sin(a-b)=\sin a\cos b-\cos a\sin b

Démonstration géométrique des formules d'addition de

cos(a + b)

sin(a + b)

Le moyen le plus rapide pour les démontrer est, à partir de la définition analytique du cosinus et du sinus, d'utiliser les formules d'Euler.

Il existe de nombreuses autres démonstrations possibles, utilisant les propriétés d'une corde dans un cercle, la relation entre cosinus d'un angle et produit scalaire (en évaluant de deux façons différentes le produit scalaire des vecteurs $(cos a, sin a)$ et $(cos b, sin b)$ , la propriété du changement de repère ou encore la démonstration matricielle ci-dessous.

Démonstration matricielle

utilise l'expression de la matrice d'une rotation plane (dans une base orthonormée directe) en fonction du cosinus et du sinus de son angle :

R_{\theta }={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{pmatrix}}.

La rotation vectorielle plane d'angle $a + b$ est la composée des rotations d'angles $a$ et $b$ donc sa matrice est le produit des matrices $R a$ et $R b$ :

${\begin{pmatrix}\cos(a+b)&\ldots \\\sin(a+b)&\ldots \\\end{pmatrix}}=R_{a+b}=R_{a}R_{b}={\begin{pmatrix}\cos a&-\sin a\\\sin a&\cos a\\\end{pmatrix}}{\begin{pmatrix}\cos b&\ldots \\\sin b&\ldots \\\end{pmatrix}}={\begin{pmatrix}\cos a\cos b-\sin a\sin b&\ldots \\\sin a\cos b+\cos a\sin b&\ldots \\\end{pmatrix}}$ .

Les formules s'obtiennent alors par identification.

On en déduit les formules d'addition et de différence pour la tangente et la cotangente. Par exemple pour l'addition[N 1] :

$\tan(a+b)={\frac {\tan a+\tan b}{1-\tan a\tan b}}\quad {\rm {et}}\quad \cot(a+b)={\frac {\cot a\cot b-1}{\cot a+\cot b}}$ .
Exemple: $\tan(x+\pi /4)={\frac {1+\tan x}{1-\tan x}}$ .

Plus généralement, la tangente d'une somme de $n$ angles[5] (resp. la cotangente) s'exprime en fonction des tangentes (resp. des cotangentes) de ces angles :

\tan(\theta _{1}+\ldots +\theta _{n})={\frac {\sigma _{1}-\sigma _{3}+\sigma _{5}-\ldots }{1-\sigma _{2}+\sigma _{4}-\ldots }}(\tan \theta _{1},\ldots ,\tan \theta _{n})\quad {\rm {et}}\quad \cot(\theta _{1}+\ldots +\theta _{n})={\frac {\sigma _{n}-\sigma _{n-2}+\sigma _{n-4}-\ldots }{\sigma _{n-1}-\sigma _{n-3}+\sigma _{n-5}-\ldots }}(\cot \theta _{1},\ldots ,\cot \theta _{n})

où les $σ k$ (pour $0 \leq k \leq n$ ) sont les polynômes symétriques élémentaires. Pour $n$ impair, il s'agit de la même fraction rationnelle ; par exemple pour $n = 3$ [N 2] :

\tan(a+b+c)=F(\tan a,\tan b,\tan c)\quad {\rm {et}}\quad \cot(a+b+c)=F(\cot a,\cot b,\cot c)\quad {\rm {avec}}\quad F(u,v,w)={\frac {u+v+w-uvw}{1-(uv+uw+vw)}}.

Une autre conséquence intéressante de la formule d'addition pour $sin$ est qu'elle permet de ramener la combinaison linéaire d'un sinus et d'un cosinus à un sinus : $\alpha \sin x+\beta \cos x={\sqrt {\alpha ^{2}+\beta ^{2}}}~\sin(x+\varphi )$ où $\varphi ={\rm {arctan}}(\beta /\alpha )$ si α est positif et $\varphi ={\rm {arctan}}(\beta /\alpha )+\pi$ sinon.

Formules de duplication et d'angle moitié

Formules de l'angle double

Appelées aussi « formules d'angle double », elles peuvent être obtenues, pour les deux premières[6], en remplaçant $a$ et $b$ par $x$ dans les formules d'addition ou en utilisant la formule de Moivre avec $n$ = 2. Les deux suivantes se déduisent de l'identité $cos 2 x + sin 2 x = 1$ .

{\begin{aligned}\sin 2x&=2\sin x\cos x,\\\cos 2x&=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x,\\\tan 2x&={\frac {2\tan x}{1-\tan ^{2}x}}={\frac {2\cot x}{\cot ^{2}x-1}}={\frac {2}{\cot x-\tan x}}.\end{aligned}}

Formules de réduction du carré

Ces formules[7] - [8] permettent d'écrire $cos 2 x$ et $sin 2 x$ , donc aussi $tan 2 x$ , en fonction du cosinus de l'angle double :

\cos ^{2}x={\frac {1+\cos(2x)}{2}},\quad \sin ^{2}x={\frac {1-\cos(2x)}{2}}\quad {\rm {et}}\quad \tan ^{2}x={\frac {1-\cos(2x)}{1+\cos(2x)}}.

Formules d'angle moitié

\left|\cos \left({\frac {\theta }{2}}\right)\right|={\sqrt {\frac {1+\cos \theta }{2}}},\qquad \left|\sin \left({\frac {\theta }{2}}\right)\right|={\sqrt {\frac {1-\cos \theta }{2}}}

\tan \left({\frac {\theta }{2}}\right)={\frac {\sin \theta }{1+\cos \theta }}={\frac {1-\cos \theta }{\sin \theta }}

Démonstration

Les deux premières identités se déduisent des formules de réduction des carrés en remplaçant $x$ par $θ /2$ .

La troisième s'obtient en écrivant $\tan \left({\frac {\theta }{2}}\right)={\frac {\sin(\theta /2)}{\cos(\theta /2)}}={\frac {2\cos(\theta /2)}{2\cos(\theta /2)}}{\frac {\sin(\theta /2)}{\cos(\theta /2)}}={\frac {\sin \theta }{1+\cos \theta }},$ où l'égalité finale vient des formules d'angle double.

La dernière (où $sin θ$ est supposé non nul) se déduit de $\sin ^{2}\theta =1-\cos ^{2}\theta =(1-\cos \theta )(1+\cos \theta ).$

Formules impliquant la « tangente de l'arc moitié »

Si l'on pose, pour $x \neq π + 2 k π$ ,

t=\tan(x/2)

on a[9]

\cos x={\frac {1-t^{2}}{1+t^{2}}}\quad {\rm {et}}\quad \sin x={\frac {2t}{1+t^{2}}}\quad {\rm {donc}}

[N 3]

{}\quad \tan x={\frac {2t}{1-t^{2}}}.

Dans le cas de changement de variable en intégration, on ajoutera la relation [9] : $\mathrm {d} x={\frac {2\,\mathrm {d} t}{1+t^{2}}}$ .

Ces formules permettent de simplifier des calculs trigonométriques en se ramenant à des calculs sur des fractions rationnelles. Elles permettent aussi de déterminer l'ensemble des points rationnels du cercle unité.

Formules de Simpson

Transformation de produits en sommes, ou linéarisation

\cos a\cos b={\frac {\cos(a+b)+\cos(a-b)}{2}}

\sin a\sin b={\frac {\cos(a-b)-\cos(a+b)}{2}}

\sin a\cos b={\frac {\sin(a+b)+\sin(a-b)}{2}}

\cos a\sin b={\frac {\sin(a+b)-\sin(a-b)}{2}}\

(équivalente à la précédente par interversion de

a

b

Ces formules peuvent être démontrées en développant leurs membres de droite en utilisant les formules d'addition et de différence.

Transformation de sommes en produits, ou antilinéarisation

\cos p+\cos q=2\cos {\frac {p+q}{2}}\cos {\frac {p-q}{2}}

\cos p-\cos q=-2\sin {\frac {p+q}{2}}\sin {\frac {p-q}{2}}

\sin p+\sin q=2\sin {\frac {p+q}{2}}\cos {\frac {p-q}{2}}

\sin p-\sin q=2\cos {\frac {p+q}{2}}\sin {\frac {p-q}{2}}

(équivalente à la précédente en remplaçant

q

par

-q

Il suffit de remplacer $a$ par $p + q / 2$ et $b$ par $p - q / 2$ dans les formules de transformation de produit en somme. On en déduit une généralisation des formules de la tangente de l'angle moitié :

\tan {\frac {p+q}{2}}={\frac {\sin p+\sin q}{\cos p+\cos q}}=-{\frac {\cos p-\cos q}{\sin p-\sin q}}

Par ailleurs, on déduit directement de la formule d'addition pour $sin$ :

\tan p+\tan q={\frac {\sin(p+q)}{\cos p\,\cos q}}

Formules d'Euler

$\cos x={\frac {{\rm {e}}^{{\rm {i}}x}+{\rm {e}}^{-{\rm {i}}x}}{2}}=\cosh {\rm {i}}x$

\sin x={\frac {{\rm {e}}^{{\rm {i}}x}-{\rm {e}}^{-{\rm {i}}x}}{2{\rm {i}}}}=-{\rm {i}}\sinh {\rm {i}}x

où $i$ est l'unité imaginaire. On en déduit que

\tan x={\frac {{\rm {i}}\left(1-{\rm {e}}^{2{\rm {i}}x}\right)}{1+{\rm {e}}^{2{\rm {i}}x}}}=-{\rm {i}}\tanh {\rm {i}}x

Formule de Moivre et formules d'angle multiple

La formule de Moivre s'écrit :

\cos(nx)+{\rm {i}}\sin(nx)=(\cos x+{\rm {i}}\sin x)^{n}

Par la formule du binôme, elle équivaut à :

\cos(nx)=\sum _{0\leq k\leq {\frac {n}{2}}}(-1)^{k}{n \choose 2k}\cos ^{n-2k}x~\sin ^{2k}x\quad {\text{et}}\quad \sin(nx)=\sum _{0\leq k\leq {\frac {n-1}{2}}}(-1)^{k}{n \choose 2k+1}\cos ^{n-2k-1}x~\sin ^{2k+1}x

Compte tenu de $sin 2 x = 1- cos 2 x$ , si l'on pose

T_{n}=\sum _{0\leq k\leq {\frac {n}{2}}}(-1)^{k}{n \choose 2k}X^{n-2k}(1-X^{2})^{k}\quad {\text{et}}\quad U_{n}=\sum _{0\leq k\leq {\frac {n-1}{2}}}(-1)^{k}{n \choose 2k+1}X^{n-2k-1}(1-X^{2})^{k}

on a $cos(nx) = T n (cos x)$ et $sin((n +1) x) = sin(x) U n (cos x)$ .

Le polynôme $T n$ (resp. $U n$ ) est le $n$ -ième polynôme de Tchebychev de première (resp. seconde) espèce.

Par exemple

\cos 3x=4\cos ^{3}x-3\cos x,\,\sin 3x=\sin x(4\cos ^{2}x-1)=-4\sin ^{3}x+3\sin x

La formule de Moivre permet aussi d'exprimer $tan(nx)$ en fonction de $tan x$ par la relation

\tan nx={\frac {{\text{Im}}(1+{\rm {i}}\tan x)^{n}}{{\text{Re}}(1+{\rm {i}}\tan x)^{n}}}

Par exemple

\tan 3x={\frac {\tan ^{3}x-3\tan x}{3\tan ^{2}x-1}}

Linéarisation

La linéarisation d'une expression $cos p x sin q x$ a pour but de l'exprimer comme combinaison linéaire de divers $cos(nx)$ (si q est pair) ou $sin(nx)$ (si q est impair) — par exemple pour en calculer une primitive. On peut utiliser soit les formules de transformation de produits en sommes ci-dessus, soit les formules d'Euler : $\cos ^{p}x\sin ^{q}x=\left({\frac {{\rm {e}}^{{\rm {i}}x}+{\rm {e}}^{-{\rm {i}}x}}{2}}\right)^{p}\left({\frac {{\rm {e}}^{{\rm {i}}x}-{\rm {e}}^{-{\rm {i}}x}}{2{\rm {i}}}}\right)^{q}.$

Il suffit ensuite de

développer chacun des deux facteurs grâce à la formule du binôme de Newton,
développer le produit des deux sommes obtenues (par distributivité),
simplifier les termes en utilisant que ${\rm {e}}^{{\rm {i}}kx}{\rm {e}}^{{\rm {i}}\ell x}={\rm {e}}^{{\rm {i}}(k+\ell )x},$
puis les regrouper, sachant que ${\rm {e}}^{{\rm {i}}nx}+{\rm {e}}^{-{\rm {i}}nx}=2\cos(nx)\quad {\rm {et}}\quad {\rm {e}}^{{\rm {i}}nx}-{\rm {e}}^{-{\rm {i}}nx}=2{\rm {i}}\sin(nx).$

Si l'un des deux exposants p ou q est nul, en appelant « degré » la valeur de l'autre, on a :

Formules de linéarisation de degré 2 ou 3

Les formules de linéarisation de degré 2 sont les « formules de réduction du carré » vues plus haut.

\cos ^{3}a={{3\cos a+\cos(3a)} \over 4}

\sin ^{3}a={{3\sin a-\sin(3a)} \over 4}

\tan ^{3}a={{3\sin a-\sin(3a)} \over {3\cos a+\cos(3a)}}

Formules de linéarisation de degré quelconque

${\begin{aligned}\cos ^{2n}x&=\left({\frac {{\rm {e}}^{{\rm {i}}x}+{\rm {e}}^{-{\rm {i}}x}}{2}}\right)^{2n}\\&={\frac {1}{2^{2n}}}\left({{2n} \choose n}+\sum _{k=0}^{n-1}{\left({{2n} \choose k}{\rm {e}}^{{\rm {i}}xk}{\rm {e}}^{-{\rm {i}}x(2n-k)}+{{2n} \choose {2n-k}}{\rm {e}}^{{\rm {i}}x(2n-k)}{\rm {e}}^{-{\rm {i}}xk}\right)}\right)\\&={\frac {1}{4^{n}}}\left({{2n} \choose n}+2\sum _{k=0}^{n-1}{{{2n} \choose k}\cos \left(2(n-k)x\right)}\right)\\\cos ^{2n+1}x&=\left({\frac {{\rm {e}}^{{\rm {i}}x}+{\rm {e}}^{-{\rm {i}}x}}{2}}\right)^{2n+1}\\&={\frac {1}{2^{2n+1}}}\sum _{k=0}^{n}{\left({{2n+1} \choose k}{\rm {e}}^{{\rm {i}}xk}{\rm {e}}^{-{\rm {i}}x(2n+1-k)}+{{2n+1} \choose {2n+1-k}}{\rm {e}}^{{\rm {i}}x(2n+1-k)}{\rm {e}}^{-{\rm {i}}xk}\right)}\\&={\frac {1}{4^{n}}}\sum _{k=0}^{n}{{2n+1} \choose k}\cos \left((2(n-k)+1)x\right)\\&={\frac {1}{4^{n}}}\sum _{\ell =0}^{n}{{2n+1} \choose {n-\ell }}\cos \left((2\ell +1)x\right)\\\bullet ~x\leftarrow &x-{\frac {\pi }{2}}&\\\sin ^{2n}x&={\frac {1}{4^{n}}}\left({{2n} \choose n}-2\sum _{\ell =0}^{n-1}{(-1)^{\ell }{{2n} \choose {n-1-\ell }}\cos \left(2(\ell +1)x\right)}\right)\\\sin ^{2n+1}x&={\frac {1}{4^{n}}}\sum _{\ell =0}^{n}(-1)^{\ell }{{2n+1} \choose {n-\ell }}\sin \left((2\ell +1)x\right)\end{aligned}}$

Calcul de sommes partielles de séries trigonométriques à coefficients constants

Les sommes $C_{n}=\sum _{k=0}^{n}\cos(k\theta +\varphi )$ et $S_{n}=\sum _{k=0}^{n}\sin(k\theta +\varphi )$ ont les expressions closes suivantes, pour $\theta \neq 0\mod 2\pi$ :

C_{n}={\frac {\sin \left((n+1){\frac {\theta }{2}}\right)}{\sin {\frac {\theta }{2}}}}\cos \left(n{\frac {\theta }{2}}+\varphi \right),\ S_{n}={\frac {\sin \left((n+1){\frac {\theta }{2}}\right)}{\sin {\frac {\theta }{2}}}}\sin \left(n{\frac {\theta }{2}}+\varphi \right)

On démontre ces formules en remarquant que $C_{n}+iS_{n}={\rm {e}}^{{\rm {i}}\varphi }\sum _{k=0}^{n}({\rm {e}}^{{\rm {i}}\theta })^{k}$ et en utilisant les sommes de suites géométriques, ou en multipliant par $\sin {\frac {\theta }{2}}$ et en linéarisant.

On en déduit que ${\frac {S_{n}}{C_{n}}}=\tan \left(n{\frac {\theta }{2}}+\varphi \right)$ .

Pour $\theta =0\mod 2\pi$ , $C_{n}=(n+1)\cos \varphi ,\,S_{n}=(n+1)\sin \varphi$ .

Ces formules permettent d'exprimer le noyau de Dirichlet $D n$ , fonction définie par :

pour tout réel

x

D_{n}(x)=1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}

Le produit de convolution de n'importe quelle fonction de carré intégrable et de période $2π$ avec le noyau de Dirichlet coïncide avec la somme d'ordre $n$ de sa série de Fourier.

Fonctions trigonométriques réciproques

Ce sont les fonctions réciproques des fonctions sinus, cosinus et tangente.

y=\arcsin x\Leftrightarrow x=\sin y\quad {\text{avec}}\quad y\in \left[{\tfrac {-\pi }{2}},{\tfrac {\pi }{2}}\right]

y=\arccos x\Leftrightarrow x=\cos y\quad {\text{avec}}\quad y\in \left[0,\pi \right]

y=\arctan x\Leftrightarrow x=\tan y\quad {\text{avec}}\quad y\in \left]{\tfrac {-\pi }{2}},{\tfrac {\pi }{2}}\right[

Si $x>0$ alors

\arctan x+\arctan {\frac {1}{x}}={\frac {\pi }{2}}

Si $x<0$ alors

\arctan x+\arctan {\frac {1}{x}}=-{\frac {\pi }{2}}

On a également l'identité suivante :

\arctan x+\arctan y=\arctan {\frac {x+y}{1-xy}}+k\pi

où

k=0\quad {\text{si}}\quad xy<1

k=1\quad {\text{si}}\quad xy>1\quad {\text{et}}\quad x>0

k=-1\quad {\text{si}}\quad xy>1\quad {\text{et}}\quad x<0

Beaucoup d'identités similaires aux suivantes peuvent être obtenues à partir du théorème de Pythagore.

Relations entre fonctions trigonométriques inverses pour $x > 0$
	arccos	arcsin	arctan	arccot
arccos		$\arccos x={\frac {\pi }{2}}-\arcsin x$	$\arccos x=\arctan {\frac {\sqrt {1-x^{2}}}{x}}$	$\arccos x=\operatorname {arccot} {\frac {x}{\sqrt {1-x^{2}}}}$
arcsin	$\arcsin x={\frac {\pi }{2}}-\arccos x$		$\arcsin x=\arctan {\frac {x}{\sqrt {1-x^{2}}}}$	$\arcsin x=\operatorname {arccot} {\frac {\sqrt {1-x^{2}}}{x}}$
arctan	$\arctan x=\arccos {\frac {1}{\sqrt {1+x^{2}}}}$	$\arctan x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}$		$\arctan x=\operatorname {arccot} {\frac {1}{x}}$
arccot	$\operatorname {arccot} x=\arccos {\frac {x}{\sqrt {1+x^{2}}}}$	$\operatorname {arccot} x=\arcsin {\frac {1}{\sqrt {1+x^{2}}}}$	$\operatorname {arccot} x=\arctan {\frac {1}{x}}$

Propriétés métriques dans un triangle quelconque

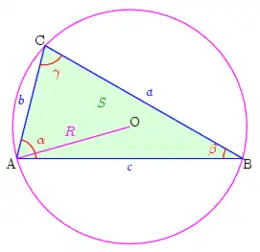
Théorème d'Al-Kashi ou loi des cosinus

Fig. 1 - Notations usuelles dans un triangle quelconque.

Soit $ABC$ un triangle, dans lequel on utilise les notations usuelles : d'une part $α$ , $β$ et $γ$ pour les mesures des angles et, d'autre part, $a$ , $b$ et $c$ pour les longueurs des côtés respectivement opposés à ces angles (voir figure ci-contre). Alors on a :

c^{2}=a^{2}+b^{2}-2ab\ \cos \ \gamma .

Formule des sinus

En notant de plus $S$ l'aire du triangle et $R$ le rayon de son cercle circonscrit (voir figure ci-contre), on a :

{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={\frac {abc}{2S}}=2R.

D'autre part, $S$ est le produit du demi-périmètre $p$ = $a + b + c / 2$ par le rayon $r$ du cercle inscrit.

Formule des différences des côtés

{\frac {a-b}{c}}={\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}\quad {\rm {et}}\quad {\frac {a+b}{c}}={\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}

{\frac {a-b}{a+b}}={\frac {\tan {\frac {\alpha -\beta }{2}}}{\tan {\frac {\alpha +\beta }{2}}}}

\cot {\frac {\alpha }{2}}={\frac {p-a}{r}}

Relations entre les angles

En utilisant le fait que $\alpha +\beta +\gamma =\pi$ on obtient de nombreuses relations trigonométriques, dont par exemple :

$\tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \tan \beta \tan \gamma$

$\sin 2\alpha +\sin 2\beta +\sin 2\gamma =4\sin \alpha \sin \beta \sin \gamma$

Identités sans variable

Richard Feynman s'est rappelé toute sa vie cette curieuse identité, qu'il appelait loi de Morrie :

\cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\tfrac {1}{8}}

Une telle identité est un exemple d'identité qui ne contient pas de variable ; elle s'obtient à partir de l'égalité :

\prod _{j=0}^{k-1}\cos(2^{j}x)={\frac {\sin(2^{k}x)}{2^{k}\sin x}}

Autres exemples :

\cos 36^{\circ }+\cos 108^{\circ }=\cos {\frac {\pi }{5}}+\cos 3{\frac {\pi }{5}}={\frac {1}{2}}.

\cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }=\cos {\frac {2\pi }{15}}+\cos 2{\frac {2\pi }{15}}+\cos 4{\frac {2\pi }{15}}+\cos 7{\frac {2\pi }{15}}={\frac {1}{2}}.

\cos {\frac {2\pi }{21}}+\cos 2{\frac {2\pi }{21}}+\cos 4{\frac {2\pi }{21}}+\cos 5{\frac {2\pi }{21}}+\cos 8{\frac {2\pi }{21}}+\cos 10{\frac {2\pi }{21}}={\frac {1}{2}}.

Les facteurs 1, 2, 4, 5, 8, 10 sont les entiers inférieurs à 21/2 qui n'ont pas de facteur commun avec 21.

Ces exemples sont des conséquences d'un résultat de base sur les polynômes cyclotomiques ; les cosinus sont les parties réelles des racines de ces polynômes ; la somme des zéros donne la valeur de la fonction de Möbius en 21 (dans le tout dernier cas qui précède) ; seulement la moitié des racines sont présentes dans ces relations.

Dans cet article, on trouvera des identités faisant intervenir l'angle ${\frac {\pi }{7}}$ , comme $\cos {\frac {\pi }{7}}-\cos {\frac {2\pi }{7}}+\cos {\frac {3\pi }{7}}={\frac {1}{2}}$
et dans celui-ci, des identités faisant intervenir l'angle $\pi \over 9$ , comme $\cos {\frac {\pi }{9}}-\cos {\frac {2\pi }{9}}+\cos {\frac {4\pi }{9}}={\frac {1}{2}}$ .
Autres identités classiques[N 4] :
- $\prod _{k=1}^{n-1}\tan {\frac {k\pi }{2n}}=1$ , dont on déduit $\tan 1^{\circ }\tan 2^{\circ }...\tan 89^{\circ }=1$ .
- $\sum _{k=1}^{n}\sin ^{2}{k{\frac {\pi }{n}}}={\frac {n}{2}}$ , dont on déduit $\sin ^{2}1^{\circ }+\sin ^{2}2^{\circ }+\cdots +\sin ^{2}89^{\circ }=\cos ^{2}1^{\circ }+\cos ^{2}2^{\circ }+\cdots +\cos ^{2}89^{\circ }=89/2$ .
- $\prod _{k=1}^{n-1}\sin {\frac {k\pi }{n}}={\frac {n}{2^{n-1}}}$ , dont on déduit $\sin 1^{\circ }\sin 2^{\circ }...\sin 89^{\circ }=\cos 1^{\circ }\cos 2^{\circ }...\cos 89^{\circ }={\sqrt {\frac {180}{2^{179}}}}$ .

En analyse

En analyse, il est essentiel que les angles qui apparaissent comme arguments de fonctions trigonométriques soient mesurés en radians ; s'ils sont mesurés en degrés ou dans n'importe quelle autre unité, alors les relations reportées ci-dessous deviennent fausses.

Encadrement

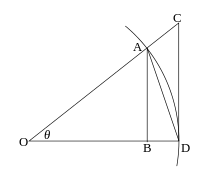
La signification géométrique du sinus et de la tangente « montre[10] » — et le théorème des accroissements finis démontre — que

\forall x\in \left]0,\pi /2\right[\quad \sin(x)<x<\tan(x).

Détails

L'argument géométrique[11] consiste (cf. figure ci-contre) à encadrer l'aire d'un secteur circulaire du disque unité, d'angle θ = x, par celle de deux triangles :
- l'aire du triangle OAD, contenu dans le secteur, vaut (sinθ)/2 ;
- celle du secteur vaut par définition θ/2 ;
- celle du triangle OCD, qui le contient, vaut (tanθ)/2.
La preuve analytique consiste à considérer un réel $y$ (fourni par le théorème des accroissements finis) tel que $0<y<x{\text{ et }}{\frac {\sin x}{x}}=\sin 'y=\cos y$ et à remarquer que $\cos x<\cos y<1.$

Cet encadrement est souvent utilisé ; deux exemples en sont la méthode d'Archimède pour le calcul du nombre $π$ (voir quadrature du cercle) et le problème de Bâle.

En changeant x en arctan x , on obtient :

\forall x>0\quad {\frac {x}{\sqrt {1+x^{2}}}}<\arctan x<x.

En changeant x en arcsin x, on obtient :

\forall x\in \left]0,1\right[\quad x<\arcsin x<{\frac {x}{\sqrt {1-x^{2}}}}.

Dérivées

Les dérivées de $sin$ et $cos$ peuvent se déduire l'une de l'autre par décalage de $π/2$ . Elles sont :

\sin '=\cos ,\quad \cos '=-\sin .

Exemples de démonstrations

Si les fonctions trigonométriques sont définies géométriquement, on se convainc d'abord de l'encadrement ci-dessus, dont on déduit immédiatement (grâce au théorème des gendarmes) $\lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1.$ Cette limite permet de calculer les dérivées de $sin$ et $cos$ , à partir de la définition du nombre dérivé comme limite d'un taux d'accroissement, en transformant la différence en produit dans le numérateur de ce taux.
Si les fonctions trigonométriques sont définies analytiquement, alors les dérivées peuvent être obtenues en dérivant les séries entières terme à terme.

Les autres fonctions trigonométriques peuvent être dérivées en utilisant les identités précédentes et les règles de dérivation. Par exemple :

$\tan '=1+\tan ^{2}={\frac {1}{\cos ^{2}}}=\sec ^{2},$ $\cot '=-1-\cot ^{2}=-{\frac {1}{\sin ^{2}}}=-\csc ^{2},$ $\arcsin '(x)={\frac {1}{\sqrt {1-x^{2}}}},$ $\arccos '=-\arcsin ',$ $\arctan '(x)={\frac {1}{1+x^{2}}}.$

Primitives

Les identités sur les intégrales peuvent être trouvées dans la table des primitives de fonctions trigonométriques.

Notes et références

Notes

Pour une démonstration du développement de $tan(a + b)$ , voir par exemple ce chapitre de la leçon « Trigonométrie » sur Wikiversité. Celui de $cot(a + b)$ se démontre de même.
Voir « Loi des cotangentes » pour une utilisation.
Sous réserve que $t$ soit différent de $\pm1$ , c'est-à-dire $x \neq π / 2 + k π$ .
Voir plus généralement cette liste d'identités sur Wikiversité.

Références

(en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne), p. 73, 4.3.45.
Arthur Adam et Francis Lousberg, Espace Math 5e/6e, De Boeck, 2003 (lire en ligne), p. 144.
Lionel Porcheron, Le formulaire MPSI, MP, Dunod, 2008, 4^e éd. (lire en ligne), p. 178.
Dany-Jack Mercier, L'épreuve d'exposé au CAPES mathématiques, vol. 2, Publibook, 2006 (lire en ligne), p. 168.
(en) Martin Erickson, Aha! Solutions, MAA, 2009 (lire en ligne), p. 30-31.
Collectif, Objectif Bac - Toutes les matières - Term STI2D, Hachette, 2014 (lire en ligne), p. 18.
Mercier 2006, p. 169.
« Formules de Carnot » (Adam et Lousberg 2003, p. 143).
Jean-Pierre Ramis, André Warusfel et al., Mathématiques Tout-en-un pour la Licence - Niveau L1, Dunod, 2^e éd. (lire en ligne), p. 676.
(en) Fred Richman, « A Circular Argument », The College Mathematics Journal (en), vol. 24, n^o 2,‎ mars 1993, p. 160-162 (lire en ligne).
Détaillé dans Fonctions trigonométriques/Propriétés préliminaires sur Wikiversité.

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.