Produit matriciel
Le produit matriciel désigne la multiplication de matrices, initialement appelé la « composition des tableaux »[1].
Produit matriciel ordinaire
Il s'agit de la façon la plus fréquente de multiplier des matrices entre elles.
En algèbre linéaire, une matrice A de dimensions m lignes et n colonnes (matrice m×n) représente une application linéaire ƒ d'un espace de dimension n vers un espace de dimension m. Une matrice colonne V de n lignes est une matrice n×1, et représente un vecteur v d'un espace vectoriel de dimension n. Le produit A×V représente ƒ(v).
Si A et B représentent respectivement les applications linéaires f et g, alors A×B représente la composition des applications .
Cette opération est utilisée notamment en mécanique lors des calculs de torseur statique, ou en informatique pour la matrice d'adjacence d'un graphe.
Le produit de deux matrices ne peut se définir que si le nombre de colonnes de la première matrice est le même que le nombre de lignes de la deuxième matrice, c'est-à-dire lorsqu'elles sont de type compatible.
Si est une matrice de type et est une matrice de type , alors leur produit, noté est une matrice de type donnée par :
La figure suivante montre comment calculer les coefficients et de la matrice produit si est une matrice de type , et est une matrice de type .
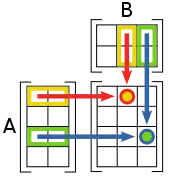
Exemples
En général, la multiplication des matrices n'est pas commutative, c'est-à-dire que n'est pas égal à , comme le montre l'exemple suivant.
- tandis que
Multiplication de matrices par bloc
Si l'on considère les matrices et , où et sont des matrices vérifiant :
- Le nombre de colonnes de et est égal au nombre de lignes de et
- Le nombre de colonnes de et est égal au nombre de lignes de et
on a alors l'égalité
On remarquera l'analogie entre le produit de matrice par blocs et le produit de deux matrices carrées d'ordre 2.
N.B. : on ne définit pas ainsi une nouvelle forme de multiplication de matrices. Cela correspond simplement à une méthode de calcul du produit matriciel ordinaire pouvant simplifier les calculs.
Produit d'Hadamard
Pour deux matrices de même type, nous avons le produit d'Hadamard ou produit composante par composante. Le produit d'Hadamard de deux matrices et de type , noté A · B = (cij), est une matrice de type donnée par
Par exemple :
Ce produit est une sous-matrice du produit de Kronecker (voir ci-dessous).
Produit de Kronecker
Pour deux matrices arbitraires et , nous avons le produit tensoriel ou produit de Kronecker A ⊗ B qui est défini par
Si est une matrice de type et est une matrice de type alors A ⊗ B est une matrice de type . À nouveau cette multiplication n'est pas commutative.
Par exemple
- .
Si et sont les matrices d'applications linéaires V1 → W1 et V2 → W2, respectivement, alors A ⊗ B représente le produit tensoriel des deux applications, V1 ⊗ V2 → W1 ⊗ W2.
Propriétés communes
Les trois multiplications matricielles précédentes sont associatives
- ,
distributives par rapport à l'addition :
et compatibles avec la multiplication par un scalaire :
Multiplication par un scalaire
La multiplication par un scalaire d'une matrice donne le produit
- .
Si nous travaillons avec des matrices sur un anneau, alors la multiplication par un scalaire est parfois appelée la multiplication à gauche tandis que la multiplication à droite est définie par :
- .
Quand l'anneau fondamental est un anneau commutatif, par exemple, le corps des réels ou des complexes, les deux multiplications sont identiques.
Cependant, si l'anneau n'est pas commutatif, tel que celui des quaternions, alors ils peuvent être différents. Par exemple
Aspects algorithmiques
Multiplication efficace de deux matrices
Le problème qui consiste, étant donné deux matrices carrées, à les multiplier rapidement, est un problème important en algorithmique. L'algorithme qui découle de la définition a une complexité en temps en , où est le nombre de lignes des matrices. Une borne inférieure est (car chacun des coefficients de la matrices doit être écrit). L'exposant optimal pour la complexité est donc compris entre 2 et 3 mais sa valeur exacte est un problème ouvert[2]. De nombreux algorithmes ont été inventés pour ce problème, citons par exemple l'algorithme de Strassen en , le premier à avoir été découvert[2], et l'algorithme de Coppersmith-Winograd en [3]. En 1993, Bahar et al. ont donné un algorithme de multiplications de matrices pour des matrices représentées symboliquement à l'aide d'une structure de données appelée Algebraic Decision Diagrams (ADD), qui est une généralisation des diagrammes de décision binaire[4].
Multiplications matricielles enchaînées
On se donne une suite de matrices rectangulaires et on souhaite en calculer le produit (on suppose que toutes les matrices ont une taille compatible, c'est-à-dire que le produit est bien défini). Le produit matriciel étant associatif, n'importe quel parenthésage du produit donnera le même résultat. Cependant le nombre de multiplications scalaires à effectuer dépend du parenthésage retenu si les matrices sont de tailles différentes.
Ainsi si l'on prend , et on a bien = mais le calcul de nécessite 6 multiplications scalaires tandis que celui de en nécessite 18.
Il peut donc être utile d'exécuter un algorithme d'optimisation de produit matriciel enchaîné afin d'identifier le parenthésage le plus efficace avant d'effectuer les produits proprement dits.
Vérification d'un produit matriciel
Pour vérifier un produit matriciel, il existe des algorithmes plus efficaces que de simplement le recalculer.
Par exemple l'algorithme de Freivalds est un algorithme probabiliste qui permet de vérifier le résultat d'un produit matriciel en avec une probabilité d'erreur aussi faible que voulue.
Notes et références
- Alain Connes, Triangle de pensées, Édition Odile Jacob, p. 72.
- (en) Thomas H. Cormen, Charles E. Leiserson et Ronald L. Rivest, Introduction à l'algorithmique, Paris, Dunod, , xxix+1146 (ISBN 978-2-10-003922-7, SUDOC 068254024), chap. 28 (« Calcul matriciel »).
- Markus Bläser, « Fast Matrix Multiplication », Theory of Computing, Graduate Surveys, vol. 5, , p. 1-60 (lire en ligne).
- R. Iris Bahar, Erica A. Frohm, Charles M. Gaona et Gary D. Hachtel, « Algebraic decision diagrams and their applications », ICCAD '93 Proceedings of the 1993 IEEE/ACM international conference on Computer-aided design, IEEE Computer Society Press, , p. 188–191 (ISBN 0818644907, lire en ligne, consulté le )



























































