Addition matricielle
L'addition matricielle est une opération mathématique qui consiste à produire une matrice qui est le résultat de l'addition de deux matrices de même type.
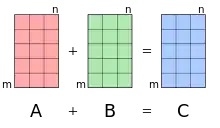
Illustration d'une addition matricielle
Processus d'addition
L'addition des matrices est définie pour deux matrices de même type.
La somme de deux matrices de type (m, n),  et
et  , notée A + B, est à nouveau une matrice
, notée A + B, est à nouveau une matrice  de type (m, n) obtenue en additionnant les éléments correspondants, i.e.,
de type (m, n) obtenue en additionnant les éléments correspondants, i.e.,
- pour tous i, j,

Par exemple:

L'ensemble des matrices de type (m, n) avec la loi d'addition forment un groupe abélien.
Cette notion d'addition des matrices provient de celle des applications linéaires; si A et B sont interprétées comme des matrices d'applications linéaires relativement à des bases données, alors la matrice somme A+B représente la matrice de la somme des deux applications linéaires par rapport à ces mêmes bases.
La somme directe
Pour toutes matrices quelconques A (de taille m × n) et B (de taille p × q), il existe la somme directe de A et B, notée  et définie par :
et définie par :

Par exemple :

Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.








