Secteur circulaire
Un secteur circulaire est la partie d'un disque délimitée par deux rayons et un arc de cercle, où la plus petite aire est connue sous le nom de secteur mineur, la plus grande étant le secteur majeur. Son domaine peut être calculé comme décrit ci-dessous.
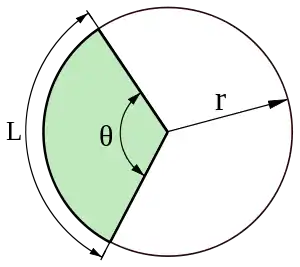
Aire
Soient θ l'angle en radians et r le rayon. La superficie totale d'un disque est π r2. La superficie du secteur circulaire peut être obtenue en multipliant la superficie du disque par le rapport entre l'angle et 2π (car l'aire d'un secteur est proportionnelle à son angle et un secteur d'angle 2π est le disque tout entier) :
De même, si a représente l'angle en degrés, on obtient :
- .
Par un raisonnement analogue, la longueur L de l'arc de cercle est donnée par la formule suivante (où a est en degrés) :
On a donc A = Lr/2.
Périmètre
La longueur P du périmètre d'un secteur circulaire, somme de la longueur d'arc et des deux rayons, est donc donnée par la formule suivante (où θ° est en degrés) :
Centre de gravité
Le centre de gravité d'un secteur angulaire est situé sur l'axe de symétrie du secteur et à une distance du sommet égale aux deux tiers de la distance entre le centre et le centre de gravité de l'arc de cercle correspondant[1]. En sachant que le centre de gravité d'un arc de cercle[2] est à une distance du centre égale à longueur de la corde ABlongueur de l'arc AB×r, on obtient les formules :
Références
- G. Ferroux et Louis Barbillon, Mécanique générale (2), albin Michel, (présentation en ligne) p.21
- Ferroux et Barbillon 1929, p. 16.




