Diagramme sagittal

En théorie des ensembles, une relation binaire d'un ensemble ${\displaystyle E}$ vers un ensemble ${\displaystyle F}$ est une application[2] lorsqu'elle est définie pour tout élément de ${\displaystyle E}$, plus précisément lorsque chaque élément de E est lié à un unique élément de F.

• 
  Application injective[3]: Tout élément de ${\displaystyle B}$ a au plus un antécédent dans ${\displaystyle A}$.
• 
  Application surjective[3]: Tout élément de ${\displaystyle B}$ a au moins un antécédent dans ${\displaystyle A}$.
• 
  Application bijective[3]: Tout élément de ${\displaystyle B}$ a un antécédent unique dans ${\displaystyle A}$.
• 
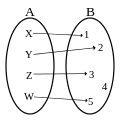
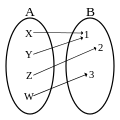
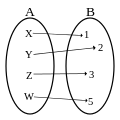
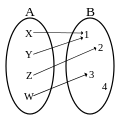  Application ni injective ni surjective.

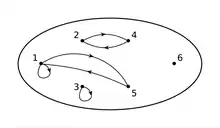
Exemple de relation d'un ensemble dans lui-même: le diagramme sagittal ci-dessous présente la relation définie sur ${\displaystyle E=\{1;2;3;4;5;6\}.}$ par ${\displaystyle a\;{\mathcal {R}}\;b\Leftrightarrow a+b{\text{ divise 6}}.}$.

Relation de ${\displaystyle E}$ dans ${\displaystyle E}$.