Axiome du choix

En mathématiques, l'axiome du choix, abrégé en « AC », est un axiome de la théorie des ensembles qui « affirme la possibilité de construire des ensembles en répétant une infinité de fois une action de choix, même non spécifiée explicitement[1]. »

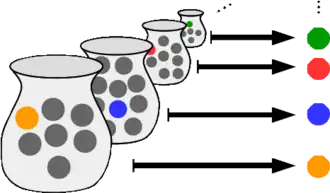
Pour tout ensemble d'ensembles non vides (les jarres), il existe une fonction qui associe à chacun de ces ensembles (ces jarres) un élément contenu dans cet ensemble (cette jarre).

Il a été formulé pour la première fois par Ernest Zermelo en 1904 pour la démonstration du théorème de Zermelo[2]. L'axiome du choix peut être accepté ou rejeté, selon la théorie axiomatique des ensembles choisie.

Énoncé

L'axiome du choix peut s'énoncer comme suit :

(0) « Pour tout ensemble X d'ensembles non vides, il existe une fonction définie sur X, appelée fonction de choix, qui à chaque ensemble A appartenant à X associe un élément de cet ensemble A. »

ce qui s'écrit formellement : $\forall X\left[\varnothing \notin X\Longrightarrow \exists f:X\rightarrow \bigcup X\;\forall A\in X\;(f(A)\in A)\right]$ [3].

L'appel à cet axiome n'est pas nécessaire si X est un ensemble fini car c'est une conséquence de la définition d'ensemble non vide (c'est-à-dire qu'il existe un élément appartenant à cet ensemble). Dans ce cas, le résultat se montre par récurrence sur le nombre d'éléments de X.

Il y a d'autres cas où une fonction de choix f peut être définie sans l'axiome du choix. Par exemple, pour un ensemble X d'ensembles non vides d'entiers naturels, on peut définir une fonction de choix en posant, pour A un élément de X, f(A) égal au plus petit élément de A (on s'est servi de la propriété de bon ordre sur les entiers naturels, et non de l'axiome du choix). Cependant dans le cas général, l'existence d'une fonction de choix repose sur l'axiome ci-dessus, par exemple pour démontrer le théorème de König.

Autres formulations

On trouve d'autres formulations de l'axiome du choix, très proches de la précédente, dont les suivantes :

(0') Pour tout ensemble E, il existe une fonction qui à chaque partie non vide de E associe un élément de cette partie.
(1) Pour toute relation d'équivalence R, il existe un système de représentants des classes de R.
(2) Toute surjection possède une section.
(3) Le produit ∏_i∈I X_i d'une famille (X_i)_i∈I d'ensembles non vides est non vide[4] - [5].

Démonstration des équivalences

(0') ⇔ (0) : (0') est un cas particulier de (0). Réciproquement, on déduit (0) de (0') en prenant comme ensemble E la réunion des ensembles appartenant à X : (0') fournit une fonction de choix sur les parties non vides de E, en particulier sur les parties appartenant à X.
(0) ⇒ (1) : soit R une relation d'équivalence sur un ensemble E. En appliquant (0) à l'ensemble X des classes d'équivalence de R, on obtient une partie F de E telle que tout élément de E est R-équivalent à un unique élément de F.
(1) ⇒ (2) : à toute surjection s : E → I est associée une relation d'équivalence R sur E : deux éléments sont équivalents s'ils ont même image par s. Un inverse à droite pour s est donné par un choix de représentants de R.
(2) ⇒ (3) : pour (X_i)_i∈I une famille d'ensembles non vides, notons E la réunion disjointe des X_i, c'est-à-dire l'ensemble de tous les couples (i, x) tels que x appartienne à X_i. Alors la première projection, de E dans I, qui à (i, x) associe i, est une surjection, dont toute section fournit un élément du produit des X_i.
(3) ⇒ (0) : soit X un ensemble d'ensembles non vides. En appliquant (3) à la famille de ces ensembles, indexée par X lui-même, on construit un élément de leur produit, c'est-à-dire une fonction de choix.

Énoncés équivalents

L'axiome du choix est souvent utilisé par l'intermédiaire de l'un des deux énoncés suivants qui lui sont équivalents :

Théorème de Zermelo : « Tout ensemble peut être muni d'un bon ordre » ;
Lemme de Zorn : « Tout ensemble inductif admet un élément maximal ».

Le théorème de Zermelo implique immédiatement l'axiome du choix : comme pour les entiers naturels (voir supra), si E est muni d'un bon ordre, le minimum pour celui-ci fournit une fonction de choix sur l'ensemble des parties non vides de E (énoncé (0')).

On montre assez facilement que le lemme de Zorn implique le théorème de Zermelo (et donc l'axiome du choix, d'après ce qui précède) et, directement mais par la même méthode, que le lemme de Zorn implique l'axiome du choix.

Il est un peu plus délicat de démontrer que l'axiome du choix implique le lemme de Zorn (et donc le théorème de Zermelo). On peut utiliser dans les deux cas assez naturellement la théorie des ordinaux, mais il est possible de démontrer le lemme de Zorn en travaillant directement sur la structure d'ordre de l'inclusion sur un ensemble de parties (c'est un ensemble inductif).

Indépendance de l'axiome du choix relativement à ZF

L'axiome du choix ne fait pas partie du jeu d'axiomes de la théorie des ensembles ZF. On appelle théorie ZFC, la théorie ZF munie en plus de l'axiome du choix.

En 1938, Kurt Gödel démontre que ZF+AC est une théorie cohérente si ZF l'est[6] - [7].

En 1963, Paul Cohen démontre que ZF+(non)AC est aussi une théorie cohérente si ZF l'est. Ce qui achève la démonstration de l’indépendance de l'axiome du choix vis-à-vis des autres axiomes de ZF.

Cet axiome fait partie des axiomes optionnels et controversés de la théorie des ensembles. En effet, l'existence d'un objet défini à partir de l'axiome du choix n'est pas une existence constructive, c’est-à-dire que l'axiome ne décrit aucunement comment construire l'objet dont on affirme l'existence[8]. Ainsi, dire qu'il existe une base de l'espace vectoriel des fonctions continues de ℝ dans ℝ ne permet en aucune façon de décrire une telle base. De ce point de vue, l'axiome du choix peut paraître d'un intérêt limité et c'est pourquoi certains mathématiciens se montrent plus satisfaits d'une démonstration s'ils peuvent éviter d'avoir recours à cet axiome du choix. Mais la plupart des mathématiciens l'utilisent sans réticence particulière.

Une illustration due à Bertrand Russell

Bertrand Russell disait à propos de l'axiome du choix : « Pour choisir une chaussette plutôt que l'autre pour chaque paire d'une collection infinie, on a besoin de l'axiome du choix. Mais pour les chaussures, ce n'est pas la peine[9]. »

Explication :

Les deux chaussettes d'une même paire sont indistinguables. Même si chaque matin on arrive à choisir celle qu'on va mettre en premier, il n'y a pas de procédé général qui permette de décider à l'avance cette infinité de choix ;
Pour les chaussures, on distingue la chaussure gauche de la chaussure droite. Ainsi, il existe une fonction de choix naturelle : par exemple, toujours choisir la chaussure gauche[10].

Exemples de théorèmes nécessitant l'axiome du choix

La première utilisation explicite de cet axiome est due à Peano, en 1890, pour démontrer l'existence de certaines solutions d'équations différentielles[11] - [12].
Le théorème de la base incomplète en dimension quelconque (et même simplement l'existence d'une base pour tout espace vectoriel[13]) n'est vrai qu'en supposant l'axiome du choix.
Le théorème de Krull (tout idéal propre d'un anneau commutatif est contenu dans un idéal maximal) est équivalent à l'axiome du choix.
Le paradoxe de Banach-Tarski est (entre autres) une conséquence de l'axiome du choix.
L'axiome du choix permet d'affirmer l'existence de parties de R non mesurables au sens de Lebesgue.
L'ensemble *R des hyperréels doit son existence à l'axiome de choix.
En théorie des graphes, les nombres chromatiques de la ligne et du plan dépendent de l'axiome du choix.
Toute surjection admet un inverse à droite.

Formes faibles de l'axiome du choix

Il existe des formes faibles de l'axiome du choix que le mathématicien utilise couramment, la plupart du temps sans s'en apercevoir[14] à moins d'être logicien ou « constructiviste », et qui servent à « construire » des suites. Elles sont absolument indispensables pour l'exposé usuel des fondements de l'analyse.

Axiome du choix dénombrable

Cet axiome, abrégé en « AC_ω », est la restriction de l'axiome du choix aux familles dénombrables :

« Étant donnée une famille dénombrable d'ensembles non vides, il existe une fonction qui à chacun d'entre eux associe un de ses éléments. »

Il est par exemple utilisé pour démontrer :

qu'une union dénombrable d'ensembles dénombrables est dénombrable[10] ;
qu'un ensemble qui n'est pas fini au sens usuel est infini au sens de Dedekind (c'est-à-dire équipotent à l'un de ses sous-ensembles stricts)[15] ;
qu'une fonction définie sur R est continue en un point x dès qu'elle est séquentiellement continue en x ;
qu'un produit dénombrable d'espaces compacts est compact ;
le théorème de Hahn-Banach pour un espace de Banach séparable ;
le théorème des fermés emboités (dont l'une des conséquences est le théorème de Baire).

Attention à une confusion courante : c'est la famille d'ensembles qui est dénombrable, aucune hypothèse n'étant faite sur les ensembles composant cette famille. L'axiome du choix dénombrable ne concerne pas la question du choix d'un élément dans un ensemble dénombrable mais la possibilité de faire une infinité dénombrable de choix simultanément.

Axiome du choix dépendant

Cet axiome, abrégé en « DC », assure que, si R est une relation sur un ensemble non vide E vérifiant

$\forall x\in E\ \exists y\in E\ xRy,$

alors il existe une suite $(x n)$ d'éléments de E telle que

$\forall n\ x_{n}Rx_{n+1}.$

Une forme plus forte de l'axiome du choix : l'epsilon de Hilbert

David Hilbert a introduit l'opérateur ε, qui à toute propriété P associe un objet εx.P(x) tel que, si P est vérifiée par au moins un élément, alors P est vérifiée par εx.P(x). Cette construction permet de définir les quantificateurs et elle est utilisée par Nicolas Bourbaki pour développer sa théorie des ensembles, avec une variante notationnelle utilisant la lettre τ (tau)[16].

Il est alors assez simple de montrer que l'axiome du choix devient un théorème, c'est-à-dire une conséquence des autres axiomes, et des règles logiques gouvernant l'emploi du tau[17]. L'opérateur tau fournit en effet une « fonction » de choix universelle, une construction (qui n'est pas une fonction au sens ensembliste) associant à tout ensemble non vide un élément de celui-ci. Tout énoncé de la théorie des ensembles de Bourbaki se traduit facilement dans une théorie des ensembles de type ZF à laquelle on a ajouté un nouveau symbole de relation, et un axiome utilisant celui-ci qui exprime que cette relation est une relation de bon ordre sur tout l'univers : le principe du choix. Le tau peut alors s'interpréter par « le plus petit x vérifiant une propriété P s’il existe ». Si cette relation n’est vérifiée par aucun objet, alors ce tau est un objet « dont on ne peut rien dire[17] ».

On associe de cette façon à tout énoncé clos démontrable dans la théorie de Bourbaki un énoncé traduit utilisant ce nouveau symbole qui est démontrable dans la théorie des ensembles ZF dont les schémas d'axiomes (on peut se restreindre au schéma d'axiomes de remplacement) ont été étendus aux énoncés contenant le nouveau symbole, et avec le principe du choix. En ajoutant l'axiome de fondation, la nouvelle théorie est conservative au-dessus de la théorie ZFC (avec axiome de fondation)[18], c'est-à-dire qu'elle ne démontre pas de nouvel énoncé du langage initial.

Notes et références

Patrick Dehornoy, chap. 4 « L'axiome du choix », dans Logique et théorie des ensembles, Notes de cours, FIMFA ENS, 2006 (lire en ligne), p. 104.
(de) E. Zermelo, « Beweis, daß jede Menge wohlgeordnet werden kann », Mathematische Annalen, vol. 59,‎ 1^er décembre 1904, p. 514–516 (DOI 10.1007/BF01445300, lire en ligne, consulté le 18 avril 2016).
Dehornoy 2006, p. 106.
Dehornoy 2006, p. 109.
(en) H. Rubin et J. E. Rubin, Equivalents of the Axiom of Choice, vol. II, North-Holland Publishing Company, 1985 (lire en ligne), p. 8.
(en) Kurt Gödel, « The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis », PNAS, vol. 24, n^o 12,‎ 1938, p. 556–557 (DOI 10.1073/pnas.24.12.556).
(en) Kurt Gödel, The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis with the Axioms of Set Theory, Princeton University Press, 1940, 72 pages, (ISBN 978-0-69107927-1) [lire en ligne].
Une telle construction est d'ailleurs démontrée impossible (en n'utilisant que les axiomes de ZF), car sinon, elle donnerait une preuve de l'axiome du choix dans ZF, contredisant le résultat de Paul Cohen.
La métaphore des chaussettes et des chaussures se trouve dans Introduction to Mathematical Philosophy de Bertrand Russell, (1993) [1919], Dover, New York (ISBN 978-0-486-27724-0), p. 125-127.
En 1963, Paul Cohen a construit un modèle (relatif) de ZF dans lequel une certaine famille dénombrable de paires n'a pas de fonction de choix, confirmant l'intuition de Russell. La réunion d'une telle famille ne peut pas être dénombrable. La même année, Solomon Feferman et Azriel Lévy ont construit un modèle (relatif) de ZF dans lequel R lui-même est réunion dénombrable d'ensembles dénombrables ((en) P. Cohen, « The Independence of the Continuum Hypothesis », PNAS, vol. 50, n^o 6,‎ 1963, p. 1143-1148 (JSTOR 71858) et (en) Paul J. Cohen, « The Independence of the Continuum Hypothesis, II », PNAS, vol. 51, n^o 1,‎ 1964, p. 105-110 (JSTOR 72252) ; (en) S. Feferman et A. Lévy, « Independence results in set theory by Cohen's method II (abstract) », Notices Amer. Math. Soc., vol. 10,‎ 1963, p. 593).
(en) Jon Barwise, Handbook of Mathematical Logic, Amsterdam/New York, Elsevier, 1989, 8^e éd., 1165 p. (ISBN 978-0-444-86388-1, lire en ligne), p. 347, citant (en) Abraham Adolf Fraenkel, Yehoshua Bar-Hillel et Azriel Lévy, Foundation of Set Theory, Amsterdam, Elsevier, coll. « Studies in Logic » (n^o 67), 1973, 2^e éd. (ISBN 978-0-7204-2270-2).
(en) John J. O'Connor et Edmund F. Robertson, « A history of set theory », sur MacTutor, université de St Andrews.
(en) Andreas Blass, « Existence of bases implies the axiom of choice » [PDF], Contemporary Mathematics, 31 (1984), 31-33.
(en) Horst Herrlich, Axiom of Choice, Springer, 2006 (lire en ligne), « Hidden Choice », p. 21-26.
Plus précisément, l'axiome du choix dénombrable est une condition suffisante (mais non nécessaire) pour que tout ensemble fini au sens de Dedekind soit fini au sens usuel : voir par exemple Herrlich 2006, chap. 4, p. 48. Par contre, dans une théorie sans axiome du choix, on montre que l'on ne peut exclure l'existence d'ensembles qui sont à la fois finis au sens de Dedekind et infinis au sens usuel.
Nicolas Bourbaki, Éléments d'histoire des mathématiques [détail des éditions], section « Fondements des mathématiques ; logique ; théorie des ensembles », sous-section « La formalisation de la logique », p. 21, écrit : « […] la plus intéressante [des modifications ingénieuses des langages formalisés actuels] est sans doute l'introduction par Hilbert du symbole : τ, qui permet de considérer comme des signes abréviateurs les quantificateurs ∃ et ∀, d'éviter l'introduction du symbole fonctionnel « universel » ι de Peano et Russell (qui ne s'applique qu'à des relations fonctionnelles), et enfin dispense de formuler l'axiome du choix dans la théorie des ensembles ([163 a], t.III, p. 183.) », la note ([163 a], t.III, p. 183.) renvoyant à : (de) D. Hilbert, Gesammelte Abhandlungen, 3 vol., Berlin (Springer), 1932-35.
N. Bourbaki, Éléments de mathématique, vol. I : Théorie des ensembles [détail des éditions], partie 1, chap. 3 (« Théories quantifiées »).
Ceci se démontre en utilisant une variante simple de la méthode de forcing, qui n'utilise pas de générique, voir Jean-Louis Krivine, Théorie des ensembles [détail des éditions], chap. 10.

Voir aussi

Liens externes

Hadamard, Borel, Baire, Lebesgue : Cinq lettres sur la théorie des ensembles (sur numdam), Bulletin de la SMF, t. 33, 1905, p. 261-273
(en) A home page for the Axiom of Choice - an introduction and links collection, par Eric Schechter, de l'université Vanderbilt
(en) Asaf Karagila, « On the partition principle », 2014
Xavier Caruso, L'axiome du choix (lire en ligne)

Ouvrages

(en) Paul Howard et Jean Rubin, Consequences of the Axiom of Choice, AMS, coll. « Mathematical Surveys and Monographs (en) » (n^o 59), 1998 (lire en ligne)
(en) Thomas J. Jech, The Axiom of Choice, Dover, 2008 (1^re éd. 1973) (lire en ligne)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.