Théorie des graphes
La théorie des graphes est la discipline mathématique et informatique qui étudie les graphes, lesquels sont des modèles abstraits de dessins de réseaux reliant des objets[1]. Ces modèles sont constitués par la donnée de sommets (aussi appelés nœuds ou points, en référence aux polyèdres), et d'arêtes (aussi appelées liens ou lignes) entre ces sommets ; ces arêtes sont parfois non-symétriques (les graphes sont alors dits orientés) et sont appelées des flèches ou des arcs.
Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette théorie ont de nombreuses applications dans tous les domaines liés à la notion de réseau (réseau social, réseau informatique, télécommunications, etc.) et dans bien d'autres domaines (par exemple génétique) tant le concept de graphe, à peu près équivalent à celui de relation binaire (à ne pas confondre donc avec graphe d'une fonction), est général. De grands théorèmes difficiles, comme le théorème des quatre couleurs, le théorème des graphes parfaits, ou encore le théorème de Robertson-Seymour, ont contribué à asseoir cette matière auprès des mathématiciens, et les questions qu'elle laisse ouvertes, comme la conjecture de Hadwiger, en font une branche vivace des mathématiques discrètes.
Définitions
Il existe plusieurs variantes dans la définition des graphes en théorie des graphes. Les définitions les plus usuelles sont les suivantes.
Graphe

Dans un sens restreint mais très répandu du terme[2] - [3], un graphe est un couple G = (V, E) comprenant
- V un ensemble de sommets (aussi appelés nœuds, points ou vertex) ;
- E ⊆ {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} un ensemble d'arêtes (aussi appelées liens ou lignes), qui sont des paires de sommets (c.-à-d. qu'une arête est associée à deux sommets distincts).
Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un graphe simple non orienté.
Dans l'arête {x, y}, les sommets x et y sont appelés les extrémités ou les sommets extrêmes de l'arête. On dit que l'arête joint x et y et est incidente sur x et sur y. Un sommet peut exister dans un graphe sans arête incidente. Les arêtes multiples sont deux arêtes ou plus qui joignent les mêmes deux sommets ; elles ne peuvent pas exister dans un graphe simple non orienté.
Dans un sens plus général du terme autorisant les arêtes multiples[4] - [5], un graphe est un triplet G = (V, E, ϕ) comprenant
- V un ensemble de sommets (aussi appelés nœuds, points ou vertex) ;
- E un ensemble d'arêtes (aussi appelés liens ou lignes) ;
- ϕ: E → {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} une fonction d'incidence associant à chaque arête une paire de sommets (c.-à-d. qu'une arête est associée à deux sommets distincts).
Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un multigraphe non orienté.
Une boucle est une arête qui joint un sommet à lui-même. Les graphes tels que définis dans les deux définitions précédentes ne peuvent pas avoir de boucles, car une boucle joignant un sommet x est l'arête (pour un graphe simple non orienté) ou est incidente sur (pour un multigraphe non orienté) {x, x} = {x} qui n'est pas dans {{x, y} | (x, y) ∈ V2 ∧ x ≠ y}. Ainsi pour autoriser les boucles les définitions doivent être étendues. Pour les graphes simples non orientés, E ⊆ {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} doit devenir E ⊆ {{x, y} | (x, y) ∈ V2}. Pour les multigraphes non orientés, ϕ: E → {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} doit devenir ϕ: E → {{x, y} | (x, y) ∈ V2}. Pour lever toute ambiguïté, ces types d'objets peuvent être appelés précisément un graphe simple non orienté avec boucles et un multigraphe non orienté avec boucles respectivement.
V et E sont en général supposés finis, et de nombreux résultats cessent d'être vrais (ou ont des énoncés différents) pour des graphes infinis parce que certains arguments de preuve ne se transposent pas au cas infini. De plus, V est souvent supposé non vide, mais E peut être l'ensemble vide. L'ordre d'un graphe |V| est son nombre de sommets. La taille d'un graphe est |E|, son nombre d'arêtes. Le degré ou la valence d'un sommet est le nombre d'arêtes incidentes à ce sommet, où une boucle compte double.
Dans un graphe simple non orienté d'ordre n, le degré maximum d'un sommet est n − 1 et la taille maximale du graphe est n(n − 1)/2.
Les arêtes E d'un graphe non orienté G induisent une relation binaire symétrique ~ sur V appelée la relation d'adjacence de G. Spécifiquement, pour chaque arête {x, y}, ses sommets extrêmes x et y sont dits adjacents l'un l'autre, ce qui est noté x ~ y.
Graphe orienté

Un graphe orienté est un graphe dans lequel les arêtes possèdent une orientation.
Dans un sens restreint mais très répandu du terme[6], un graphe orienté est un couple G = (V, A) (parfois G = (V, E)) comprenant
- V un ensemble de sommets (aussi appelés nœuds ou points) ;
- A ⊆ {(x, y) | (x, y) ∈ V2 ∧ x ≠ y} un ensemble de flèches (aussi appelées arêtes orientées — parfois simplement arêtes avec l'ensemble correspondant nommé E au lieu de A —, liens orientés ou lignes orientées), qui sont des couples de sommets distincts (c.-à-d. une flèche est associée à deux sommets distincts).
Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un graphe simple orienté.
Dans la flèche (x, y) orientée de x vers y, x est appelé la queue de la flèche et y la tête de la flèche. La flèche (y, x) est appelée la flèche inverse de (x, y).
Dans un sens plus général du terme autorisant les flèches multiples[4] - [5], un graphe orienté est un triplet G = (V, A, ϕ) (parfois G = (V, E, ϕ)) comprenant
- V un ensemble de sommets (aussi appelés nœuds ou points) ;
- A un ensemble de flèches (aussi appelées arêtes orientées — parfois simplement arêtes avec l'ensemble correspondant nommé E au lieu de A —, liens orientés ou lignes orientées);
- ϕ: A → {(x, y) | (x, y) ∈ V2 ∧ x ≠ y} une fonction d'incidence associant à chaque flèche un couple de sommets distincts (c.-à-d. une flèche est associée à deux sommets distincts).
Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un multigraphe orienté.
Les graphes orientés tels que définis dans les deux définitions précédentes ne peuvent pas avoir de boucles, car une boucle joignant un sommet x est la flèche (pour un graphe simple orienté) ou est incidente sur (pour un multigraphe orienté) (x, x) qui n'est pas dans {(x, y) | (x, y) ∈ V2 ∧ x ≠ y}. Ainsi pour autoriser les boucles les définitions doivent être étendues. Pour les graphes simples orientés, A ⊆ {(x, y) | (x, y) ∈ V2 ∧ x ≠ y} doit devenir A ⊆ V2. Pour les multigraphes orientés, ϕ: A → {(x, y) | (x, y) ∈ V2 ∧ x ≠ y} doit devenir ϕ: A → V2. Pour lever toute ambiguïté, ces types d'objets peuvent être appelés précisément un graphe simple orienté avec boucles et un multigraphe orienté avec boucles (ou un carquois) respectivement.
Un graphe simple orienté avec boucles est une relation homogène (une relation binaire entre un ensemble et lui-même). Un graphe simple orienté avec boucles G = (V, A) est dit symétrique si, pour chaque flèche de A, la flèche inverse correspondante appartient aussi à A.
Topologies

Il existe trois grandes familles de graphes et cinq catégories au total :
- structurés : il est alors possible de définir quatre identités topologiques remarquables :
- homogènes (1) : les sommets et les arêtes reproduisent un schéma régulier. Le schéma le plus commun est une architecture de type matriciel aussi appelé "en filet de poisson" (mesh) ;
- hiérarchiques (2) : structure typique des graphes où les sommets s'arrangent en couches hiérarchisées et pyramidales ;
- cycliques (3) : on peut identifier des cycles dans le graphe. L'exemple le plus parlant est le graphe circulaire ;
- centralisés ou polaires (4) : c'est une architecture où tous les sommets sont rattachés à un seul sommet, le pôle ;
- quelconques (5) : aucune propriété topologique ne semble émerger ;
- multipolaires : c'est une architecture mixte entre les graphes centralisés et décentralisés. Les réseaux multipolaires sont très étudiés en raison de leur proximité avec de nombreux cas concrets, notamment Internet ou les réseaux de neurones. Les graphes multipolaires sont caractérisés par deux types d'arêtes : celles qui forment les liens émanant du pôle : les liens forts ; et les liens réunissant deux pôles entre eux : les liens faibles. Les pôles peuvent par ailleurs prendre une architecture structurée (souvent centralisée) ou quelconque.
Origines
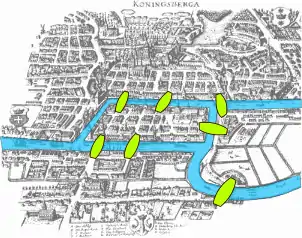
Un article du mathématicien suisse Leonhard Euler, présenté à l'Académie de Saint-Pétersbourg en 1735 puis publié en 1741, traitait du problème des sept ponts de Königsberg[O 1], ainsi que schématisé ci-dessous. Le problème consistait à trouver une promenade à partir d'un point donné qui fasse revenir à ce point en passant une fois et une seule par chacun des sept ponts de la ville de Königsberg. Un chemin passant par toute arête exactement une fois fut nommé chemin eulérien, ou circuit eulérien s'il finit là où il a commencé. Par extension, un graphe admettant un circuit eulérien est dit graphe eulérien, ce qui constitue donc le premier cas de propriété d'un graphe. Euler avait formulé[7] qu'un graphe n'est eulérien que si chaque sommet a un nombre pair d'arêtes. L'usage est de s'y référer comme théorème d'Euler, bien que la preuve n'en ait été apportée que 130 ans plus tard par le mathématicien allemand Carl Hierholzer[O 2]. Un problème similaire consiste à passer par chaque sommet exactement une fois, et fut d'abord résolu avec le cas particulier d'un cavalier devant visiter chaque case d'un échiquier par le théoricien d'échecs arabe Al-Adli dans son ouvrage Kitab ash-shatranj paru vers 840 et perdu depuis[O 3]. Ce problème du cavalier fut étudié plus en détail au XVIIIe siècle par les mathématiciens français Alexandre-Théophile Vandermonde[O 4], Pierre Rémond de Montmort et Abraham de Moivre; le mathématicien britannique Thomas Kirkman étudia le problème plus général du parcours où on ne peut passer par un sommet qu'une fois, mais un tel parcours prit finalement le nom de chemin hamiltonien d'après le mathématicien irlandais William Rowan Hamilton, et bien que ce dernier n'en ait étudié qu'un cas particulier[O 5]. On accorde donc à Euler l'origine de la théorie des graphes parce qu'il fut le premier à proposer un traitement mathématique de la question, suivi par Vandermonde.
 →
→
 →
→


Au milieu du XIXe siècle, le mathématicien britannique Arthur Cayley s'intéressa aux arbres, qui sont un type particulier de graphe n'ayant pas de cycle, i.e. dans lequel il est impossible de revenir à un point de départ sans faire le chemin inverse. En particulier, il étudia le nombre d'arbres à n sommets[O 6] et montra qu'il en existe . Ceci constitua « une des plus belles formules en combinatoire énumérative »[O 7], domaine consistant à compter le nombre d'éléments dans un ensemble fini, et ouvrit aussi la voie à l'énumération de graphes ayant certaines propriétés. Ce champ de recherche fut véritablement initié par le mathématicien hongrois George Pólya, qui publia en 1937 le théorème de dénombrement qui porte son nom, et le mathématicien hollandais Nicolaas Govert de Bruijn. Les travaux de Cayley, tout comme ceux de Polya, présentaient des applications à la chimie et le mathématicien anglais James Joseph Sylvester, coauteur de Cayley, introduisit en 1878 le terme de "graphe" basé sur la chimie :
« Il peut ne pas être entièrement sans intérêt pour les lecteurs de Nature d'être au courant d'une analogie qui m'a récemment fortement impressionné entre des branches de la connaissance humaine apparemment aussi dissemblables que la chimie et l'algèbre moderne. […] Chaque invariant et covariant devient donc exprimable par un graphe précisément identique à un diagramme Kékuléan ou chemicographe[O 8]. »

Un des problèmes les plus connus de théorie des graphes vient de la coloration de graphe, où le but est de déterminer combien de couleurs différentes suffisent pour colorer entièrement un graphe de telle façon qu'aucun sommet n'ait la même couleur que ses voisins. En 1852, le mathématicien sud-africain Francis Guthrie énonça le problème des quatre couleurs par une discussion à son frère, qui demandera à son professeur Auguste De Morgan si toute carte peut être coloriée avec quatre couleurs de façon que des pays voisins aient des couleurs différentes. De Morgan envoya d'abord une lettre au mathématicien irlandais William Rowan Hamilton, qui n'était pas intéressé, puis le mathématicien anglais Alfred Kempe publia une preuve erronée[O 9] dans l’American Journal of Mathematics, qui venait d'être fondé par Sylvester. L'étude de ce problème entraîna de nombreux développements en théorie des graphes, par Peter Guthrie Tait, Percy John Heawood, Frank Ramsey et Hugo Hadwiger.
Les problèmes de factorisation de graphe émergèrent ainsi à la fin du XIXe siècle en s'intéressant aux sous-graphes couvrants, c'est-à-dire aux graphes contenant tous les sommets mais seulement une partie des arêtes. Un sous-graphe couvrant est appelé un k-facteur si chacun de ses sommets a k arêtes et les premiers théorèmes furent donnés par Julius Petersen[O 10] ; par exemple, il montra qu'un graphe peut être séparé en 2-facteurs si et seulement si tous les sommets ont un nombre pair d'arêtes (mais il fallut attendre 50 ans pour que Bäbler traite le cas impair[O 11]). Les travaux de Ramsey sur la coloration, et en particulier les résultats du mathématicien hongrois Pal Turan, permirent le développement de la théorie des graphes extrémaux s'intéressant aux graphes atteignant le maximum d'une quantité particulière (par exemple le nombre d'arêtes) avec des contraintes données[O 12], telles que l'absence de certains sous-graphes.
Dans la seconde moitié du XXe siècle, le mathématicien français Claude Berge contribue au développement de la théorie des graphes par ses contributions sur les graphes parfaits[O 13] et l'introduction du terme d’hypergraphe (à la suite de la remarque de Jean-Marie Pla l'ayant utilisé dans un séminaire) avec un monographe[O 14] sur le sujet. Son ouvrage d'introduction à la théorie des graphes[O 15] proposa également une alternative originale, consistant plus en une promenade personnelle qu'une description complète. Il marquera également la recherche française en ce domaine, par la création conjointe avec Marcel-Paul Schützenberger d'un séminaire hebdomadaire à l'Institut Henri Poincaré, des réunions le lundi à la Maison des Sciences de l'Homme, et la direction de l'équipe Combinatoire de Paris.
Flots dans les réseaux
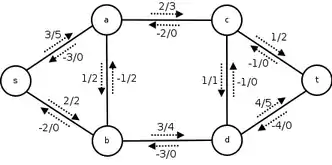


Les Allemands Franz Ernst Neumann et Jacobi, respectivement physicien et mathématicien, fondèrent en 1834 une série de séminaires. Le physicien allemand Gustav Kirchhoff était un des étudiants participant au séminaire entre 1843 et 1846, et il étendit le travail de Georg Ohm pour établir en 1845 les lois de Kirchhoff exprimant la conservation de l'énergie et de la charge dans un circuit électrique. En particulier, sa loi des nœuds stipule que la somme des intensités des courants entrant dans un nœud est égale à celle qui en sort. Un circuit électrique peut se voir comme un graphe, dans lequel les sommets sont les nœuds du circuit, et les arêtes correspondent aux connexions physiques entre ces nœuds. Pour modéliser les courants traversant le circuit, on considère que chaque arête peut être traversée par un flot. Ceci offre de nombreuses analogies, par exemple à l'écoulement d'un liquide comme l'eau à travers un réseau de canaux[Flot 1], ou la circulation dans un réseau routier. Comme stipulé par la loi des nœuds, le flot à un sommet est conservé, ou identique à l'entrée comme à la sortie ; par exemple, l'eau qui entre dans un canal ne disparaît pas et le canal n'en fabrique pas, donc il y a autant d'eau en sortie qu'en entrée. De plus, une arête a une limite de capacité, tout comme un canal peut transporter une certaine quantité maximale d'eau. Si l'on ajoute que le flot démarre à un certain sommet (la source) et qu'il se termine à un autre (le puits), on obtient alors les principes fondamentaux de l'étude des flots dans un graphe.
Si on considère que la source est un champ pétrolifère et que le puits est la raffinerie où on l'écoule, alors on souhaite régler les vannes de façon à avoir le meilleur débit possible de la source vers le puits. En d'autres termes, on cherche à avoir une utilisation aussi efficace que possible de la capacité de chacune des arêtes, ce qui est le problème de flot maximum. Supposons que l'on « coupe » le graphe en deux parties, telles que la source est dans l'une et le puits est dans l'autre. Chaque flot doit passer entre les deux parties, et est donc limité par la capacité maximale qu'une partie peut envoyer à l'autre. Trouver la coupe avec la plus petite capacité indique donc l'endroit où le réseau est le plus limité, ce qui revient à établir le flot maximal qui peut le traverser[Flot 2]. Ce théorème est appelé flot-max/coupe-min et fut établi en 1956.
L’étude des flots réseaux se généralise de plusieurs façons. La recherche d'un maximum, ici dans le cas du flot, est un problème d'optimisation, qui est la branche des mathématiques consistant à optimiser (i.e. trouver un minimum ou maximum) une fonction sous certaines contraintes. Un flot réseau est soumis à trois contraintes[Flot 3] : la limite de capacité sur chaque arête, la création d'un flot non nul entre la source et le puits (i.e. la source crée un flot), et l'égalité du flot en entrée/sortie pour tout sommet autre que la source et les puits (i.e. ils ne consomment ni ne génèrent une partie du flot). Ces contraintes étant linéaires, le problème d'un flot réseau fait partie de l'optimisation linéaire. Il est également possible de rajouter d'autres variables au problème pour prendre en compte davantage de situations : on peut ainsi avoir plusieurs sources et puits, une capacité minimale (en) sur chaque arête, un coût lorsqu'on utilise une arête, ou une amplification du flot (en) passant par une arête.
Introduction de probabilités

Jusqu'au milieu du XXe siècle, l'algorithme construisant un graphe n'avait rien d'aléatoire : tant que les paramètres fournis à l'algorithme ne changeaient pas, alors le graphe qu'il construisait était toujours le même. Une certaine dose d'aléatoire fut alors introduite, et les algorithmes devinrent ainsi probabilistes. Le mathématicien d'origine russe Anatol Rapoport eut d'abord cette idée en 1957[Proba 1] mais elle fut proposée indépendamment deux ans après, de façon plus formelle, par les mathématiciens hongrois Paul Erdős et Alfréd Rényi[Proba 2]. Ceux-ci se demandèrent à quoi ressemble un graphe « typique » avec n sommets et m arêtes. Ils souhaitaient ainsi savoir quelles propriétés pouvaient être trouvées avec n sommets, et m arêtes créées au hasard. Une quantité fixe m n'étant pas pratique pour répondre à cette question[Proba 3], il fut décidé que chaque arête existerait avec une probabilité p. Ceci fut le début de la théorie des graphes aléatoires, où l'on considère un nombre de sommets n assez grand, et l'on s'intéresse à la probabilité p suffisante pour que le graphe ait une certaine propriété.

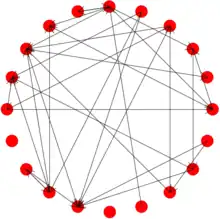
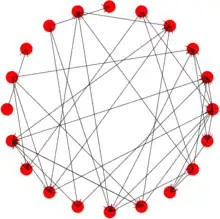
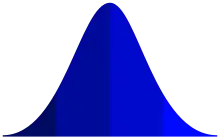
Erdős et Rényi découvrirent que le graphe n'évoluait pas de façon linéaire mais qu'il y avait au contraire une probabilité critique p après laquelle il changeait de façon radicale. Ce comportement est bien connu en physique : si l'on observe un verre d'eau que l'on met dans un congélateur, il ne se change pas progressivement en glace mais plutôt brutalement lorsque la température passe en dessous de 0 °C. L'eau avait deux phases (liquide et glace) et passe de l'une à l'autre par un phénomène nommé transition de phase, la transition étant rapide autour d'un point critique qui est dans ce cas la température de 0 °C. Pour nombre de propriétés observées, les graphes aléatoires fonctionnent de la même manière[Proba 4] : il existe une probabilité critique en dessous de laquelle ils se trouvent dans une phase sous-critique, et au-dessus de laquelle ils passent en phase sur-critique. Dans le cas d'un graphe aléatoire, la probabilité que l'on observe la propriété nous intéressant est faible en phase sous-critique mais devient très forte (i. e. quasi-certitude) en phase sur-critique ; le tracé de la probabilité d'avoir la propriété en fonction de p a donc une allure bien particulière, simplifiée dans le schéma à droite.
Au-delà du vocabulaire commun des phases, la théorie des graphes aléatoires se retrouve en physique statistique sous la forme de la théorie de la percolation[Proba 5]. Cette dernière visait à l'origine à étudier l'écoulement d'un fluide à travers un matériau poreux. Par exemple, si l'on immerge une pierre ponce dans un seau rempli d'eau[Proba 6], on s'intéresse à la façon dont l'eau va s'écouler dans la pierre. Pour modéliser ce problème, on se concentre sur les paramètres importants : l'âge ou la couleur de la pierre n'importe pas, tandis que les ouvertures ou 'canaux' dans lesquels peut circuler l'eau sont primordiaux. L'abstraction la plus simple est de voir une pierre comme une grille, où chaque canal existe avec une probabilité p. On retrouve ainsi le modèle du graphe aléatoire, mais avec une contrainte spatiale : une arête ne peut exister entre deux sommets que s'ils sont voisins dans la grille. Cependant, cette contrainte peut être levée pour établir une équivalence entre la théorie des graphes et celle de la percolation. Tout d'abord, un graphe de n sommets peut être représenté par une grille avec n dimensions ; puisqu'on s'intéresse au cas où n est assez grand, c'est-à-dire , ceci établit une équivalence avec la percolation en dimension infinie. De plus, il existe une dimension critique telle que le résultat ne dépend plus de la dimension dès que celle-ci atteint ; on pense que cette dimension critique est 6, mais elle n'a pu être prouvée[Proba 7] que pour 19.
De nombreux modèles ont été proposés depuis le début des années 2000 pour retrouver des phénomènes observés dans des graphes tels que celui représentant les connexions entre des acteurs de Hollywood (obtenu par IMDb) ou des parties du Web. En 1999, Albert-László Barabási et Réka Albert expliquèrent qu'un de ces phénomènes « est une conséquence de deux mécanismes : le réseau grandit continuellement avec l'ajout de nouveaux sommets, et les nouveaux sommets s'attachent avec certaines préférences à d'autres qui sont déjà bien en place »[Proba 8]. Une certaine confusion s'installa autour de leur modèle : s'il permet effectivement d'obtenir le phénomène souhaité, il n'est pas le seul modèle arrivant à ce résultat et on ne peut donc pas conclure en voyant le phénomène qu'il résulte d'un processus d'attachement préférentiel. Les phénomènes de petit monde et de liberté d'échelle, pour lesquels de très nombreux modèles ont été proposés, peuvent être réalisés simplement par des graphes aléatoires[Proba 9] : la technique de Michael Molloy et Bruce Reed[Proba 10] permet d'obtenir l'effet de libre d'échelle, tandis que celle de Li, Leonard et Loguinov conduit au petit-monde[Proba 11].
Représentations et invariants
Étiquetage et morphismes
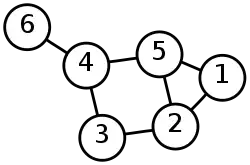
Formellement un graphe est étiqueté : chaque sommet ou arête appartient à un ensemble, donc porte une étiquette. Typiquement, les graphes sont étiquetés par des nombres entiers, mais une étiquette peut en fait appartenir à n'importe quel ensemble : ensemble de couleurs, ensemble de mots, ensemble des réels. Les exemples ci-contre montrent des graphes étiquetés par des entiers et par des lettres. L'étiquetage d'un graphe peut être conçu de façon à donner des informations utiles pour des problèmes comme le routage : partant d'un sommet , on veut arriver à un sommet , c'est-à-dire que l'on souhaite acheminer une information de à . Selon la façon dont les sommets sont étiquetés, les étiquettes que portent et peuvent nous permettre de trouver facilement un chemin. Par exemple, dans le graphe de Kautz (en) où la distance maximale entre deux sommets est , imaginons que l'on soit à un sommet étiqueté et que l'on souhaite aller à : il suffit de décaler l'étiquette en introduisant la destination[R 1], ce qui donne le chemin
Ce chemin se lit de la façon suivante : si on se trouve au sommet étiqueté alors on va vers le voisin portant l'étiquette , et ainsi de suite.
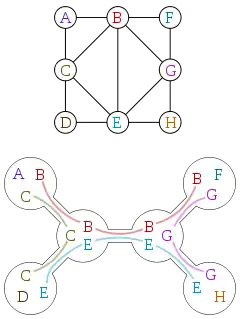
On se retrouve cependant face à un problème : si on regarde plus haut l'illustration de la liste des arbres à 2, 3 et 4 sommets, beaucoup d'entre eux ont exactement la même structure mais un étiquetage différent (donné ici par des couleurs). Pour étudier uniquement la structure, il faut donc un outil permettant d'ignorer l'étiquetage, c'est-à-dire de donner une équivalence structurelle. Pour cela, on introduit la notion de morphisme. Un morphisme de graphes[R 2], ou homomorphisme de graphes, est une application entre deux graphes qui respecte la structure des graphes. Autrement dit l'image du graphe dans doit respecter les relations d'adjacences présentes dans . Plus précisément, si et sont deux graphes, une application est un morphisme de graphes si où transforme les sommets de G en ceux de H, et les arêtes de G en celles de H en respectant la contrainte suivante : s'il existe une arête entre deux sommets de alors il doit y avoir une arête entre les deux sommets correspondants de . On dit de l'homomorphisme qu'il est une injection (respectivement surjection) si ses deux fonctions et sont injectives (respectivement surjectives); si elles sont à la fois injectives et surjectives, c'est-à-dire bijectives, alors est un isomorphisme de graphes. Si deux graphes sont isomorphes, alors ils ont la même structure : peu importe la façon dont ils sont dessinés ou étiquetés, il est possible de déplacer les sommets ou de changer les étiquettes pour que l'un soit la copie conforme de l'autre, ainsi qu'illustré ci-dessous. On désigne alors par graphe non étiqueté la classe d'équivalence d'un graphe pour la relation d'isomorphisme. Deux graphes isomorphes seront alors considérés comme égaux si on les considère en tant que graphes non étiquetés.
| Graphe G | Graphe H | Isomorphisme entre G et H |
|---|---|---|
 |
 |
Le mot graphe peut désigner, selon les contextes, un graphe étiqueté ou non étiqueté. Quand on parle du graphe du web, les étiquettes sont des URL et ont un sens. Le mot est utilisé pour désigner un graphe étiqueté. À l'opposé le graphe de Petersen est toujours considéré à isomorphisme près, donc non étiqueté, seules ses propriétés structurelles étant intéressantes.
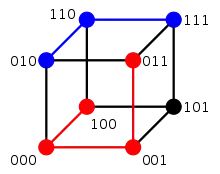
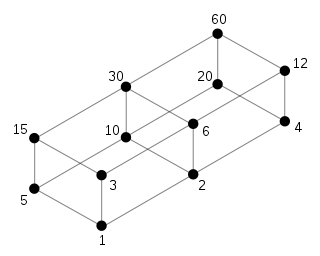 Graphe étiqueté par des entiers
Graphe étiqueté par des entiers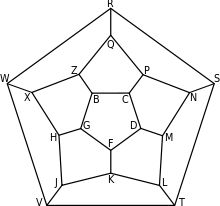 Graphe étiqueté par des lettres
Graphe étiqueté par des lettres
Graphes et algèbre linéaire
Tout graphe peut être représenté par une matrice. Les relations entre arêtes et sommets, appelées les relations d'incidence, sont toutes représentées par la matrice d'incidence du graphe. Les relations d'adjacences (si deux sommets sont reliés par une arête ils sont adjacents) sont représentés par sa matrice d'adjacence. Elle est définie par
| Graphe | Représentation par une matrice d'adjacence | Représentation par une matrice laplacienne (non normalisée) |
|---|---|---|
 |
De nombreuses informations d'un graphe peuvent être représentées par une matrice. Par exemple, la matrice des degrés est une matrice diagonale où les éléments correspondent au nombre de connexions du sommet , c'est-à-dire à son degré. En utilisant cette matrice et la précédente, on peut également définir la matrice laplacienne ; on obtient sa forme normalisée par , où dénote la matrice identité, ou on peut aussi l'obtenir directement par chacun de ses éléments :
Ces représentations dépendent de la façon dont les sommets du graphe sont étiquetés. Imaginons que l'on garde la même structure que dans l'exemple ci-dessus et que l'on inverse les étiquettes 1 et 6 : on inverse alors les colonnes 1 et 6 de la matrice d'adjacence. Il existe en revanche des quantités qui ne dépendent pas de la façon dont on étiquette les sommets, tels que le degré minimal/maximal/moyen du graphe. Ces quantités sont des invariants du graphe : elles ne changent pas selon la numérotation. Tandis qu'une matrice d'adjacence ou laplacienne varie, son spectre, c'est-à-dire l'ensemble de ses valeurs propres , est un invariant. L'étude du rapport entre les spectres et les propriétés d'un graphe est le sujet de la théorie spectrale des graphes[R 3] ; parmi les rapports intéressants, le spectre donne des renseignements sur le nombre chromatique, le nombre de composantes connexes et les cycles du graphe.
Décompositions arborescentes et en branches
Les graphes permettant de représenter de nombreuses situations, il existe de nombreux algorithmes (i.e. programmes) les utilisant. La complexité d'un algorithme consiste essentiellement à savoir, pour un problème donné, combien de temps est nécessaire pour le résoudre et quel est l'espace machine que cela va utiliser. Certaines représentations de graphes permettent d'obtenir de meilleures performances, c'est-à-dire que le problème est résolu plus rapidement ou en occupant moins d'espace. Dans certains cas, un problème NP-complet (classe la plus ardue) sur une représentation d'un graphe peut être résolu en temps polynomial (classe simple) avec une autre représentation; l'idée n'est pas qu'il suffit de regarder le graphe différemment pour résoudre le problème plus vite, mais que l'on « paye » pour le transformer et que l'on « économise » alors pour résoudre le problème. Une telle transformation est la décomposition arborescente proposée par les mathématiciens Robertson et Seymour dans leur série Graph Minors[R 4]. Intuitivement, une décomposition arborescente représente le graphe d'origine par un arbre, où chaque sommet correspond à un sous-ensemble des sommets de G, avec quelques contraintes. Formellement, pour un graphe donné , sa décomposition arborescente est où est un arbre et une fonction associant à chaque sommet un ensemble de sommets . Trois contraintes doivent être satisfaites :
- . La décomposition n'oublie aucun sommet du graphe d'origine.
- tel que .
- si est sur le chemin de à alors . Si l'on prend l'intersection des sommets abstraits par deux nœuds de l'arbre, alors cette intersection doit être contenue dans un sommet intermédiaire. Sur l'exemple ci-contre, l'intersection de {A,B,C} et {C,D,E} est {C} qui est bien contenue dans le sommet intermédiaire {C,B,E}.
La largeur arborescente d'une décomposition d'un graphe est , c'est-à-dire la taille du plus grand ensemble représenté par un sommet moins 1 ; on peut la voir comme l'abstraction maximale : pour un sommet de l'arbre, jusqu'à combien de sommets du graphe représente-t-on ? Construire la décomposition arborescente d'un graphe quelconque avec la plus petite largeur arborescente est un problème NP-dur[R 5]. Cependant, cela peut être fait rapidement pour certains graphes[R 6], ou approximée[R 7] pour d'autres tels les graphes planaires (i. e. pouvant être dessinés sans croiser deux arêtes).

Robertson et Seymour développèrent également le concept de décomposition en branches. Pour la comprendre, il faut introduire davantage de vocabulaire sur un arbre. Dans les graphes, un arbre est dessiné "à l'envers" : on démarre de la racine en haut, et on descend jusqu'à atteindre les feuilles en bas ; tout sommet n'étant pas une feuille est appelé un 'nœud interne'. La décomposition en branches résulte en un arbre dans lequel tout nœud interne a exactement trois voisins (comme sur l'exemple ci-contre), et où chaque feuille représente une arête du graphe d'origine. La profondeur minimale de la décomposition d'un graphe est notée , et on a la relation . De même que pour la décomposition arborescente, il est NP-dur de construire une décomposition en branches avec minimal pour un graphe quelconque ; dans ce cas, cette construction est réalisable pour un graphe planaire[R 8].
Ces représentations sont utilisées sur des problèmes NP-complets par des techniques de programmation dynamique, qui prennent généralement un temps exponentiel en ou . Un tel problème est par exemple l'ensemble dominant : on veut savoir s'il y a un sous-ensemble de sommets de taille au plus tel qu'un sommet n'étant pas dans y soit relié par une arête. Si le graphe est planaire, cette technique permet de résoudre le problème[R 9] en temps .
Aspect algorithmique
Structures de données
La façon dont le graphe est représenté en tant qu'objet mathématique a été exposée dans la section précédente. Dans l'aspect algorithmique de la théorie des graphes, on cherche à concevoir un processus efficace pour traiter un problème faisant intervenir un graphe. Les principaux critères d'efficacités d'un processus sont le temps nécessaire avant d'obtenir la réponse, et l'espace que le processus consomme dans son travail. La façon dont on représente le graphe influence la performance en temps et en espace : par exemple, si l'on veut connaître l'existence d'une arête entre deux sommets, la matrice d'adjacence permettra d'obtenir un résultat immédiatement, ce que l'on appelle en . En revanche, une opération de base telle que trouver le voisin d'un sommet est en sur une matrice d'adjacence : dans le pire des cas, il faudra scanner la totalité de la colonne pour s'apercevoir qu'il n'y a pas de voisin. Une autre structure de données est la liste d'adjacence, consistant en un tableau dont l'entrée donne la liste des voisins du sommet : sur une telle structure, trouver un voisin se fait en tandis que l'existence d'une arête est en . Ainsi, au niveau du temps, le choix de la structure dépend des opérations de base que l'on souhaite optimiser.

| Représentation par liste d'adjacence du graphe ci-contre: | ||
| 0 | adjacent à | 0,1,2,3 |
| 1 | adjacent à | 0 |
| 2 | adjacent à | 0,3,4 |
| 3 | adjacent à | 0,2 |
| 4 | adjacent à | 2 |
De même, l'espace qu'une structure consomme dépend du type de graphe considéré : un raccourci abusif consiste à dire qu'une liste d'adjacences consomme moins d'espace qu'une matrice car celle-ci sera creuse, mais cela prend par exemple plus d'espace pour stocker un graphe aléatoire avec les listes qu'avec une matrice ; dans le cas général, une matrice utilise un espace et les listes utilisent donc si le graphe est dense alors peut être suffisamment grand pour qu'une matrice consomme moins d'espace, et si le graphe est peu dense alors les listes consommeront moins d'espace. Des modifications simples d'une structure de données peuvent permettre d'avoir un gain appréciable : par exemple, dans une représentation partiellement complémentée d'une liste, un bit spécial indique si la liste est celle des voisins présents ou manquants ; cette technique permet d'avoir des algorithmes linéaires sur le complément d'un graphe[Algo 1].
Tandis que ces structures sont locales, il existe aussi des structures de données distribuées. Le principe de ces structures est de concevoir un schéma d'étiquetage tel que, pour deux sommets et , on puisse répondre à une question comme « quelle est la distance entre et » uniquement en utilisant les étiquettes de ces nœuds ; une telle utilisation des étiquettes a été vue en section « Étiquetage et morphismes » avec le graphe de Kautz où l'on peut déduire le chemin entre deux sommets uniquement grâce à leur étiquette, et la longueur de ce chemin nous donne la distance. Un étiquetage est efficace s'il permet de répondre à une question donnée uniquement en utilisant deux étiquettes, tout en minimisant le nombre maximum de bits d'une étiquette[Algo 2]. Outre la distance, une question type peut être de tester l'adjacence, c'est-à-dire de savoir si deux sommets sont voisins ; notons que cela se ramène également au cas particulier d'une distance 1. Le premier exemple d'étiquetage efficace pour tester l'adjacence fut proposé dans le cas des arbres, et chaque étiquette est constituée de deux parties de bits : la première partie identifie le sommet, et un nombre allant jusqu'à nécessite bits pour être codé, tandis que la seconde partie identifie le parent de ce sommet ; pour tester l'adjacence, on utilise le fait que deux sommets sont voisins dans un arbre si et seulement si l'un est le parent de l'autre[Algo 3].
Sous-graphes utiles : séparateurs, spanners et arbres de Steiner
L'efficacité d'un schéma d'étiquetage est lié à la taille des séparateurs du graphe.
Définition — un séparateur est un sous-ensemble de sommet qui « sépare » les sommets du graphe en deux composants et tel que et il n'y a pas d'arêtes entre des sommets de et .
Si un graphe a des séparateurs de taille , alors on peut par exemple concevoir des étiquettes de bits pour la distance ; ceci permet directement d'en déduire l'étiquetage pour des graphes dont on connaît la taille des séparateurs, tels un graphe planaire où le séparateur est de taille [Algo 4]. Enfin, il ne faut pas considérer que la taille de l'étiquetage mais également le temps nécessaire, étant donnés deux étiquettes, pour effectuer le décodage répondant à la question (i.e. quelle est la distance ? sont-ils voisins ?).
Réduction de données
De nombreux problèmes sur les graphes sont NP-complets, c'est-à-dire durs à résoudre. Cependant, cette dureté est inégale : certaines parties du problème peuvent être particulièrement dures, et en constituent ainsi le cœur, tandis que d'autres sont assez faciles à gérer. Ainsi, avant d'exécuter un algorithme sur un problème qui peut être dur, il est préférable de passer du temps à réduire ce problème pour ne plus avoir à considérer que son cœur.
Notions connexes
- Un graphe est également un espace topologique de dimension 1 dont la généralisation est un complexe simplicial.
- Un graphe biparti est un graphe dont l'ensemble de sommets peut être partitionné en deux sous-ensembles et tels que chaque arête ait une extrémité dans et l'autre dans .
Notes
- Il existe d'autres objets mathématiques portant le même nom, par exemple les graphes de fonctions, mais ceux-ci n'ont que peu de rapports avec les graphes étudiés ici.
- (en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, , 251 p. (lire en ligne), p. 148
- Par exemple (Iyanaga et Kawada 1977, p. 234) ou (Biggs 1993, p. 4).
- (en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, , 251 p. (lire en ligne), p. 149
- Par exemple (Graham et. al. 1995, p. 5).
- (en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, , 251 p. (lire en ligne), p. 161
- Au regard des mathématiques modernes, la formulation d'Euler est une conjecture puisque le résultat est énoncé sans preuve. Cependant, les mathématiques en son temps ne présentaient pas la même rigueur : tandis que conjecturer un résultat signifie maintenant que l'on renonce à le démontrer, pour Euler l'absence d'une preuve peut signifier que celle-ci n'était pas considérée utile.
Références
Origines
- (la) Leonhard Euler - Solutio problematis ad geometriam situs pertinentis, Commentarii academiae scientiarum Petropolitanae 8, 1741, pages 128-140.
- (de) Carl Hierholzer, « Über die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren », dans Mathematische Annalen, vol. 6, 1873, p. 30–32
- (en) Martin G. - The arab role in the development of Chess, Al Shindagah 45, Mars-Avril 2002
- Alexandre-Théophile Vandermonde, « Remarques sur des problèmes de situation », dans Mémoires de l’Académie Royale des Sciences, 1771, p. 566-574. Références par (ru) LJ.Rossia.org
- (en) William Tutte - Graph theory as I have known it, Oxford Science Publications, Clarendon Press, 1998, (ISBN 978-0-19-850251-7). Chapitre 2 : Knight Errant.
- (en) Arthur Cayley, « On the Theory of the Analytical Forms called Trees », dans Phil. Mag., 1857, p. 172-176
- Martin Aigner et Günter M. Ziegler, « La formule de Cayley pour le nombre d’arbres », dans Raisonnements divins, 2e éd., 2006
- (en) James Joseph Sylvester, « Chemistry and algebra », dans Nature, no 17, 7 février 1878, p. 284
- (en) Alfred Bray Kempe, « On the Geographical Problem of the Four Colours », dans American Journal of Mathematics, vol. 2, no 3, septembre 1879, p. 193-200
- (de) Julius Petersen, « Die Theorie der regulären Graphen », dans Acta Mathematica, vol. 15, 1891, p. 193-220
- (de) F. Bäbler, « Über die Zerlegung regulärer Streckencomplexe ungerader Ordnung », dans Comment. Math. Helv., vol. 10, 1938, p. 275–287
- (en) Bela Bollobas, Extremal Graph Theory, Dover, 2004
- (en) Claude Berge, « Some classes of perfect graphs », dans « Six papers on Graph Theory », Indian. Statistical Institute, Calcutta, 1969, p. 1-21
- Claude Berge, Graphes et hypergraphes, Dunod, 1970
- Claude Berge, Théorie des graphes et ses applications, Dunod, 1958
Flots
- (en) V.V. Ostapenko et A. P. Yakovleva, « Mathematical questions of modeling and control in water distribution problems », dans Control Cybern., vol. 20, no 4, 1991, p. 99-111
- (en) Kevin Wayne, Diaporama présentant l'équivalence entre la coupe minimale et le flot maximal. Support d'étude pour le livre Algorithm Design de Jon Kleinberg et Éva Tardos, Addison Wesley, 2005.
- (en) John W. Chinneck, Practical optimization: a gentle introduction, 2001, chap. 10
Probabilités
- (en) Anatol Rapoport, « Contribution to the theory of random and biased nets », dans Bulletin of Mathematical Biology, vol. 19, no 4, 1957
- (en) Paul Erdős et Alfréd Rényi, « On random graphs », dans Publicationes Mathematicae, vol. 6, 1959. Voir également des mêmes auteurs : « On the evolution of random graphs », dans Publications of the Mathematical Institute of the Hungarian Academy of Sciences, vol. 5, 1960.
- (en) Rick Durrett, Random Graph Dynamics, Cambridge Series in Statistical and Probabilistic Mathematics, 2006, chap. 1
- (en) A. V. Lapshin, « The property of phase transitions in random graphs », dans Probabilistic Methods in Discrete Mathematics: Proceedings of the Third International Petrozavodsk Conference, Petrozavodsk, Russia, May 12-15, 1992
- (en) Bela Bollobas et Oliver Riordan, Percolation, Cambridge University Press, 2006. Cet ouvrage présente la théorie de la percolation avec une approche inspirée de la théorie des graphes.
- (en) Harry Kesten, « What is percolation? », dans Notices Amer. Math. Soc., vol. 53, no 5, 2006
- (en) Takashi Hara et Gordon Slade, « Mean-field critical behaviour for percolation in high dimensions », dans Commun. Math. Phys., vol. 128, 1990
- (en) Albert-László Barabási et Reka Albert, « Emergence of scaling in random networks », dans Science, no 286, 1999
- (en) Philippe Giabbanelli, Self-improving immunization policies for epidemics over complex networks, thèse de master, Université Simon Fraser, 2009, sous la direction de Joseph G. Peters
- (en) Michael Molloy et Bruce A. Reed, « A critical point for random graphs with a given degree sequence », dans Random Struct. Algorithms, vol. 6, no 2/3, 1995, p. 161–180
- (en) Xiafeng Li, Derek Leonard et Dmitri Loguinov, « On Reshaping of Clustering Coefficients in Degree-Based Topology Generators », dans Algorithms and Models for the Web-Graph, Berlin, Springer, 2004, p. 68-79
Représentations
- J-C. Bermond et al., Communications dans les réseaux de processeurs, Masson, 1994 (ISBN 978-2-225-84410-2). Paru sous le pseudonyme Jean de Rumeur.
- (en) Pavol Hell et Jaroslav Nesetril, Graphs and Homomorphisms, Oxford University Press, 2004 (ISBN 978-0-19-852817-3)
- (en) Fan R. K. Chung, Spectral Graph Theory, coll. Regional Conference Series in Mathematics, no 92, AMS, 1997.
- (en) Neil Robertson et Paul D. Seymour, « Graph Minors II Algorithmic Aspects of Tree-Width », dans Journal of Algorithms, vol. 7, no 3, 1983
- (en) S. Arnborg, D.G. Corneil et A. Proskurowski, « Complexity of finding embedding in a k-tree », dans SIAM Journal on Discrete Mathematics, vol. 8, 1987, p. 277-284
- (en) Hans L. Bodlaender, « A linear time algorithm for finding tree-decomposition of small treewidth », dans SIAM journal on Computing, vol. 25, 1996, p. 1305-1317
- (en) Paul D. Seymour et R. Thomas, « Call routing and the ratcatcher », dans Combinatorica, vol. 14, no 2, 1994, p. 217-241
- (en) Q.P. Gu et H. Tamaki, « Optimal branch decomposition of planar graphs in time », dans Proceedings of the 32nd International Colloquium on Automata, Languages, and Programming, LNCS 3580, Springer-Verlag, 2005, p. 373-384
- Pour les notations et techniques, voir (en) Qianping Gu, « Tree/Branch Decompositions and Their Applications »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), notes de cours à l'Université Simon Fraser.
Aspect algorithmique
- [PDF] (en) Elias Dahlhaus, Jens Gustedt et Ross M. McConnell, « Partially complemented representations of digraphs », dans Discrete Mathematics and Theoretical Computer Science, vol. 5, no 1, 2002, p. 147-168
- (en) Stephen Alstrup et Theis Rauhe, « Small Induced-Universal Graphs and Compact Implicit Graph Representations », dans Proceedings of the 43rd annual IEEE Symposium on Foundations of Computer Science, 2002, p. 53-62
- (en) Sampath Kannan, Moni Naor, et Steven Rudich, « Implicit Representation of Graphs », dans SIAM J. on Discrete Math., vol. 5, 1992, p. 596-603
- (en) Cyril Gavoille, David Peleg, Stéphane Pérennes et Ran Razb, « Distance labeling in graphs », dans Journal of Algorithms, vol. 53, 2004, p. 85-112
Bibliographie
- Olivier Cogis et Claudine Schwartz, Théorie des graphes : problèmes, théorèmes, algorithmes, Paris, Cassini, , 280 p. (ISBN 978-2-84225-189-5)
- Alain Bretto, Alain Faisant et François Hennecart, Éléments de théorie des graphes, Paris, Springer-Verlag France, coll. « IRIS », , xix + 371 (ISBN 978-2-8178-0280-0 et 978-2-8178-0281-7, zbMATH 1250.68002).
- Johannes Carmesin, « Graph Theory – A Survey on the Occasion of the Abel Prize for László Lovász », Jahresbericht der Deutschen Mathematiker-Vereinigung, vol. 124, , p. 83-108 (DOI 10.1365/s13291-022-00247-7
 )
)
Voir aussi
Articles connexes
- DOT est un outil en langage pour décrire des graphes de façon abstraite, ainsi qu'un outil en ligne de commande permettant d'exporter des graphes en images (JPEG, GIF, PNG) ou en dessin vectoriel SVG.
- Géomatique
- Voyages au pays des maths
- Sous-graphe
- Théorie topologique des graphes
- Graphe (type abstrait)
- RDF
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :
- (en) « Metanet », sur Scilab ATOMS (consulté le ) : boîte à outils Scilab pour les graphes et réseaux

















































































