Complexe simplicial

En mathématiques, un complexe simplicial est un objet géométrique déterminé par une donnée combinatoire et permettant de décrire certains espaces topologiques en généralisant la notion de triangulation d'une surface. Un tel objet se présente comme un graphe avec des sommets reliés par des arêtes, sur lesquelles peuvent se rattacher des faces triangulaires, elles-mêmes bordant éventuellement des faces de dimension supérieure, etc.

Exemple d'un complexe simplicial.

Cette structure est particulièrement utile en topologie algébrique, car elle facilite le calcul des groupes d'homologie de certains espaces comme les polyèdres et certaines variétés topologiques qui admettent une décomposition en complexe simplicial.

La structure de complexe simplicial est enrichie dans celle d'ensemble simplicial, puis généralisée par celle de CW-complexe en autorisant des rattachements de faces non combinatoires.

Approche géométrique

Définition

La définition de complexe simplicial géométrique[1] fait appel à celle de simplexe affine. Dans un espace affine réel de dimension n, un simplexe est défini comme l'enveloppe convexe d'un ensemble de n+1 points dont aucun ne peut être obtenu comme barycentre des autres. Ces points sont appelés les sommets du simplexe. L'ensemble des sommets peut être déduit du simplexe comme étant l'ensemble de ses points extrémaux. Par exemple, un triangle ou un tétraèdre sont des simplexes, ayant respectivement 3 et 4 sommets. Un segment est aussi un simplexe dont les deux sommets sont ses extrémités.

Les faces d'un simplexe sont les enveloppes convexes des sous-ensembles des sommets. Le terme « face » comprend donc ici les sommets (singletons), les arêtes, les faces triangulaires et ainsi de suite en dimension supérieure.

Un complexe simplicial géométrique est un ensemble K de simplexes d'un espace affine tel que :

toutes les faces de chaque simplexe de K appartiennent aussi à K ;
l'intersection de deux simplexes non disjoints doit exactement être une de leurs faces communes. Elle est l'enveloppe convexe de leurs sommets communs.

L'exemple le plus simple d'un complexe simplicial est l'ensemble des faces d'un simplexe. Ainsi, un triangle est composé de trois sommets, trois côtés et une surface intérieure. Dans l'espace, un tétraèdre est composé de quatre sommets, de six arêtes, de quatre faces triangulaires et d'un volume intérieur.

Polyèdre et triangulation

Le polyèdre associé à un complexe simplicial géométrique K est simplement la réunion de tous les simplexes qu'il contient. Il est noté |K|. La donnée d'un complexe simplicial et d'un homéomorphisme entre son polyèdre et un espace topologique X constitue une triangulation de X.

Ainsi un cube ne se présente pas naturellement comme un complexe simplicial, notamment parce que ses faces ne sont pas triangulaires, mais il admet plusieurs triangulations possibles parce que chaque face peut être divisée en deux triangles.

Application simpliciale

Une application simpliciale entre deux complexes simpliciaux est une application continue entre leurs polyèdres qui associe aux sommets de chaque simplexe des sommets d'un même simplexe (sans être nécessairement injective) et dont la restriction à chaque simplexe est affine. Une telle application est donc complètement déterminée par les images des sommets.

Ces applications simpliciales permettent d'approcher n'importe quelle application continue entre deux espaces triangulés.

Approche combinatoire

Puisque chaque simplexe est entièrement déterminé par l'ensemble de ses sommets, un complexe simplicial géométrique peut être identifié à l'aide d'un objet combinatoire associé : le complexe simplicial abstrait.

Définition

Un complexe simplicial abstrait est la donnée d'un ensemble V (dont les éléments sont appelés sommets) et d'un ensemble Σ de parties finies non vides (les faces) de V qui soit stable par sous-parties non vides. Autrement dit, toute partie non vide d'une face est aussi une face. Il est en général requis que tout sommet appartienne à un nombre fini non nul de faces.

Les faces de cardinal 2 sont aussi appelées arêtes en référence au vocabulaire de la théorie des graphes. Par analogie, pour tout entier n, une face de dimension n (dite aussi n-face) est une face de cardinal n + 1.

Si la dimension des faces est bornée, la dimension d'un complexe simplicial est la dimension maximale des faces. Dans le cas contraire, cette dimension est infinie. Le f-vecteur d'un complexe simplicial abstrait de dimension d est par définition la suite finie (f₀ = 1, f₁, …, f_{d + 1}) où f_{n + 1} est le nombre de n-faces. Une caractérisation des suites finies d'entiers qui sont des f-vecteurs est donnée par le théorème de Kruskal-Katona.

Un complexe de dimension 0 est donc simplement un ensemble sans structure additionnelle. Un complexe de dimension 1 est un graphe.

La relation de sous-complexe est définie par l'inclusion de l'ensemble des sommets et l'inclusion de l'ensemble des faces.

Cas particuliers et opérations

Sur tout ensemble X sans structure additionnelle, il existe un unique complexe simplicial (combinatoire) de dimension 0. Il s'agit de l'ensemble des singletons de X. Sa réalisation topologique est X muni de la topologie discrète.
Sur tout ensemble fini non vide V de cardinal n + 1, il existe un unique complexe simplicial de dimension n, défini par l'ensemble des sous-parties finies de V. Sa réalisation topologique est un simplexe de dimension n.
Plus généralement, pour tout ensemble V et pour tout entier naturel n, l'ensemble 𝒫_n(V) des parties de V de cardinal au plus n + 1 forme un complexe simplicial de dimension n.
Pour tout entier naturel n, le n-squelette d'un complexe simplicial (V, Σ) est défini par l'ensemble des faces de dimension inférieure ou égale à n. Autrement dit, Σ_n = Σ ⋂ 𝒫_n(V).
La restriction d'un complexe simplicial à un sous-ensemble de sommets est défini par l'ensemble des faces incluses dans ce sous-ensemble. Autrement dit, Σ_|W = 𝒫(W) ⋂ Σ.
La réunion de deux complexes simpliciaux ayant des ensembles de sommets disjoints est définie par les réunions de faces (α∪β) où α et β sont des faces respectives des complexes initiaux.
La subdivision barycentrique (en) d'un complexe simplicial K = (V, Σ) a pour sommets les faces de K et pour faces les ensembles finis non vides de faces de K totalement ordonnés par l'inclusion. La subdivision barycentrique d'un triangle plein est ainsi composée de sept sommets, de douze arêtes et de six faces triangulaires.

Réalisation géométrique

Étant donné un complexe simplicial K = (V ; Σ), sa réalisation géométrique (notée |K|) est un espace topologique construit par recollement de simplexes, qui étendent en toute dimension la suite : segment, triangle, tétraèdre…

Constructions

Puisque l'intersection de deux simplexes du complexe doit être une de leurs faces communes, un point de |K| est identifié de façon unique comme barycentre de certains sommets de V (il y aurait plusieurs barycentres possibles si les simplexes s'inter-pénétraient). Une première méthode de construction est donc l'ensemble des coordonnées barycentriques :

|K|=\left\{\lambda :V\to [0,1]\;\;/\;{\text{Supp}}(\lambda )\in \Sigma \;{\text{ et }}\sum _{v\in V}\lambda (v)=1\right\}

où Supp(λ), le support de λ, est l'ensemble des sommets de V où λ est non nulle, ie les sommets qu'elle utilise pour barycentrer.

Reste à munir |K| d'une topologie. Si l'ensemble V des sommets est de cardinal s fini, |K| est une partie de l'hypercube [0,1]^s et hérite de sa topologie. Si V est infini, la topologie à considérer n'est pas la topologie produit mais la topologie cohérente ou topologie faible. L'adjectif « faible » (en anglais : weak) se retrouve dans le « W » de CW-complexe. Concrètement, on souhaite que les faces de jointure soient des fermés non ouverts de |K|, ce qui amène à définir sa topologie par ses fermés :

{\mathcal {F}}(|K|)=\left\{F\subset |K|\;\;/\;\;\forall \sigma \in \Sigma ,\;F\cap \sigma {\text{ fermé de }}\sigma \right\}

Une autre méthode consiste à définir une union disjointe de tous les simplexes à l'aide de coordonnées barycentriques puis à la quotienter de façon à réaliser le recollement, autrement dit :

\forall \alpha \in \Sigma ,\ \Delta _{\alpha }=\left\{\lambda \in (\mathbb {R} ^{+})^{\alpha },\sum _{v\in \alpha }\lambda (v)=1\right\},

\forall \beta \subset \alpha ,\ \forall \lambda \in \Delta _{\alpha },\ (\lambda _{|\alpha -\beta }=0\Rightarrow \lambda \sim \lambda _{|\beta })

|K|=\bigsqcup _{\alpha \in \Sigma }\Delta _{\alpha }/\sim .

L'intérêt de cette seconde méthode est qu'elle s'étend à la réalisation des ensembles simpliciaux.

Propriétés

Cette topologie confère à |K| une structure de CW-complexe. En particulier, un complexe simplicial est un espace topologique séparé et même normal. Une partie de cet espace est fermée si et seulement si son intersection avec chaque cellule (ici les cellules sont les n-faces) est fermée.

Un complexe simplicial de dimension 0 est un espace topologique discret.
Un complexe simplicial de dimension 1 est un graphe.
Un complexe simplicial de dimension 2 est un espace triangulé.
Plus généralement, en toute dimension, on appelle triangulation d'un espace topologique un homéomorphisme entre cet espace et un complexe simplicial. Bien sur, tout espace topologique n'est pas triangulable.

Cette construction historique est assez restrictive :

Dans cette construction, les sommets d'une face sont distincts ; de plus, deux faces ne peuvent pas avoir exactement les mêmes sommets. Il faut par exemple au minimum 14 triangles, 21 arêtes et 7 sommets pour trianguler un tore (ce qui donne le polyèdre de Császár). D'où l'idée de lever ces restrictions. Cela mène à la structure de ∆-complexe. Avec cette nouvelle structure, deux triangles suffisent pour représenter un tore, une sphère ou un plan projectif. le calcul des groupes d'homologie s'en trouve grandement simplifié.

∆-complexe

Les ∆-complexes généralisent les complexes simpliciaux avec une construction similaire à celle des CW-complexes.

On appelle simplexe standard ∆_n de dimension n l'enveloppe convexe dans ℝⁿ des points $e_{0}$ , $e_{1}$ , ..., $e_{n}$ , où $e_{0}=(0,...,0)$ et où $e_{i}=(0...,0,1,0,...,0)$ , le 1 étant placé à la i-ème position. L'ordre des sommets du simplexe standard a ici une importance capitale : non seulement, il oriente le simplexe lui-même mais en plus, il fournit automatiquement une orientation automatique de toutes les faces ; Le signe de l'orientation intervient dans la définition du bord ci-dessous.

Pour définir un ∆-complexe, on commence par prendre la réunion disjointe d'une famille de simplexes standards disjoints (de dimension variable) . On quotiente alors l'espace topologique obtenu par une relation d'équivalence que l'on définit de la façon suivante : On choisit arbitrairement une collection de familles de faces de même dimension (une dimension par famille de faces), chaque face faisant partie de l'un des simplexes dont on vient de faire la réunion disjointe (rien n'empêche de prendre plusieurs faces du même simplexe). On identifie alors toutes les faces de chaque famille en utilisant les applications linéaires préservant l'ordre des sommets. Notez qu'un effet collatéral est l'identification de certains sommets.

Les ∆-complexes peuvent sembler plus généraux que les complexes simpliciaux mais en fait tout ∆-complexe est homéomorphe à un complexe simplicial. Il suffit en effet d'effectuer deux subdivisions barycentrique successives pour transformer un ∆-complexe en complexe simplicial.

Exemples

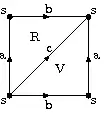
Le tore - Il est possible de trianguler le tore avec un sommet s, trois arêtes a,b,c et deux faces R et V. On part de la représentation classique du tore par un carré dont on recolle les côtés opposés et on coupe ce carré en deux pour obtenir des triangles. On obtient ainsi une structure de ∆-complexe. La bouteille de Klein peut aussi être triangulée de la même façon, mais en inversant le sens d'une des connexions entre les deux triangles.
Le ruban de Moebius - Le ruban de Moebius diffère du tore de deux manières. D'une part, on ne recolle qu'un bord du carré, le deuxième bord reste libre. D'autre part, on fait pivoter avant de recoller. D'où le diagramme ci-contre. Cette fois, on a deux sommets s et t, quatre arêtes a, b, c et d et toujours deux faces R et V.
Le plan projectif - Le plan projectif est plus difficile à visualiser vu qu'il ne se plonge pas dans l'espace usuel. On l'obtient en recollant les bords du ruban de Moebius suivant le diagramme. Il existe une autre façon de recoller qui elle donne une bouteille de Klein. (Dans ce cas il n'y aura qu'un seul sommet comme pour le tore.) Ici, on a deux sommets s et t, trois arêtes a, b, c et deux faces R et V.

Le tore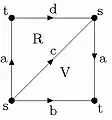
Le ruban de Moebius
Le plan projectf

Homologie simpliciale

Considérons un ∆-complexe X = (A₀, … , A_n) où A₀ est l'ensemble des sommets et A_n l'ensemble des n-faces.

Pour chaque entier naturel n, on note ∆_n(X) le groupe abélien libre de base A_n. Les éléments de ∆_n(X) seront appelés les n-chaines. En d'autre termes, une n-chaine est une combinaison linéaire à coefficients entiers de n-faces du complexe X.

On définit le bord d'un simplexe de la façon suivante :

\partial [s_{0},\dots ,s_{n}]=\sum _{i=0}^{n}(-1)^{i}[s_{0},\dots ,s_{i-1},s_{i+1}\dots ,s_{n}].

Par exemple :

Le bord d'un segment est égal à son extrémité moins son origine : ∂[a, b] = [b] – [a] ;
le bord d'un triangle est égal à la somme des trois côtés avec un signe moins tenant compte de l'orientation : ∂[a, b, c] = [a, b] – [a, c] + [b, c] ;
le bord d'un tétraèdre est donné par la formule : ∂[a, b, c, d] = [b, c, d] – [a, c, d] + [a, b, d] – [a, b, c].

Par linéarité, le bord se prolonge en un morphisme de groupes ∂_n de ∆_n(X) vers ∆_n–1(X). On a ∂_n–1∘∂_n = 0 et l'on obtient ainsi un complexe de chaînes. Les groupes d'homologie de l'espace X sont les H_k(X) = ker ∂_k / lm ∂_k+1.

Même si ce n'est pas évident a priori, si deux ∆-complexes sont homéomorphes et plus généralement, s'ils ont le même type d'homotopie, alors leurs groupes d'homologie sont identiques.

Calculs effectifs

On peut vérifier sur quelques exemples que le calcul des groupes d'homologie d'un espace triangulé par un ∆-complexe est un jeu d'enfants.

Homologie du tore

Dans le cas du tore T, $\Delta _{0}(T)=\mathbb {Z} .s$ , $\Delta _{1}(T)=\mathbb {Z} .a\oplus \mathbb {Z} .b\oplus \mathbb {Z} .c$ et $\Delta _{2}(T)=\mathbb {Z} .R\oplus \mathbb {Z} .V$ . L'application $\delta _{1}:\Delta _{1}(T)\to \Delta _{0}(T)$ est nulle (voir le schéma). D'autre part $\delta _{2}(R)=c-b-a$ et $\delta _{2}(V)=b+a-c$ .

Vu que $\delta _{1}=0$ , on a $H_{0}(T)=\Delta _{0}(T)\sim \mathbb {Z}$ . D'autre part $Im\;\delta _{2}=\mathbb {Z} .(a+b-c)$ et $Ker\;\delta _{2}=\mathbb {Z} .(R-V)$ , ce qui donne $H_{1}(T)=\Delta _{1}(T)/Im\;\delta _{2}\sim \mathbb {Z} ^{2}$ et $H_{2}(T)=Ker\;\delta _{2}\sim \mathbb {Z}$ .

On peut interpréter les choses ainsi : $H_{0}(T)=\mathbb {Z}$ signifie que T est connexe. $H_{1}(T)=\mathbb {Z} ^{2}$ signifie que T se referme sur lui-même dans deux directions différentes. $H_{2}(T)=\mathbb {Z}$ signifie que T enferme un volume.

Homologie du ruban de Moebius

Dans le cas du ruban de Moebius, M, $\Delta _{0}(M)=\mathbb {Z} .s\oplus \mathbb {Z} .t$ , $\Delta _{1}(M)=\mathbb {Z} .a\oplus \mathbb {Z} .b\oplus \mathbb {Z} .c\oplus \mathbb {Z} .d$ et $\Delta _{2}(M)=\mathbb {Z} .R\oplus \mathbb {Z} .V$ .

$\delta _{1}(a)=\delta _{1}(b)=t-s,\ \delta _{1}(c)=0,\ \delta _{1}(d)=s-t$ et donc $H_{0}(M)=\Delta _{0}(M)/Im\ \delta _{1}\sim \mathbb {Z}$ .

On a $Ker\ \delta _{1}=\mathbb {Z} .c+\mathbb {Z} (b-a)+\mathbb {Z} (a+d)$ et $Im\ \delta _{2}=\mathbb {Z} .(b-a-c)+\mathbb {Z} .(c-d-a)$ . Finalement $H_{1}(M)\sim \mathbb {Z}$ .

$\delta _{2}$ est injective donc $H_{2}(M)=0$ .

Homologie du plan projectif

Dans le cas du plan projectif, P, $\Delta _{0}(P)=\mathbb {Z} .s\oplus \mathbb {Z} .t$ , $\Delta _{1}(P)=\mathbb {Z} .a\oplus \mathbb {Z} .b\oplus \mathbb {Z} .c$ et $\Delta _{2}(P)=\mathbb {Z} .R\oplus \mathbb {Z} .V$ .

$\delta _{1}(a)=\delta _{1}(b)=t-s,\ \delta _{1}(c)=0$ et donc $H_{0}(P)=\Delta _{0}(P)/Im\ \delta _{1}\sim \mathbb {Z}$ .

On a $Ker\ \delta _{1}=\mathbb {Z} .c+\mathbb {Z} (b-a)$ et $Im\ \delta _{2}=\mathbb {Z} .(-a+b+c)+\mathbb {Z} .(a-b+c)$ . Finalement $H_{1}(P)\sim \mathbb {Z} /2\mathbb {Z}$ . il y a une petite finesse ici, c n'est pas dans $Im\ \delta _{2}$ mais 2c y est.

$\delta _{2}$ est injective donc $H_{2}(P)=0$ .

Résultats généraux

$H_{0}(X)$ est un groupe abélien libre engendré par les composantes connexes de X.
Si X a plusieurs composantes connexes $(X_{i})_{i\in I},H_{n}(X)=\oplus _{i\in I}H_{n}(X_{i})$ .
Si X est connexe, $H_{1}(X)$ est l'abélianisé du groupe fondamental $\pi _{1}(X)$ .
En notant $S^{n}$ la sphère de dimension n, on a $H_{0}(S^{n})=\mathbb {Z}$ , $H_{n}(S^{n})=\mathbb {Z}$ et $H_{p}(S^{n})=0$ dans tous les autres cas.

Notes et références

(en) Glen E. Bredon (en), Topology and Geometry [détail de l’édition], Definition IV.21.1 sur Google Livres.

Voir aussi

Bibliographie

(en) James W. Alexander, « The combinatorial theory of complexes », Ann. Math., 2^e série, vol. 31, n^o 2,‎ 1930, p. 292-320 (JSTOR 1968099)
(en) Allen Hatcher, Algebraic Topology, New York, CUP, 2001, 544 p. (ISBN 978-0-521-79540-1, lire en ligne) — On y trouvera tout sur les ∆-complexes et l'homologie simpliciale.
(en) Edwin Spanier, Algebraic Topology, Springer Verlag, 1994 (ISBN 978-0-38794426-5) — Les complexes simpliciaux y sont étudiés en détail.

Lien externe

Victor Mouquin, « Complexes simpliciaux et triangulation », sur EPFL, 2006

Article connexe

Topologie numérique

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.