Cube
En géométrie euclidienne, un cube est un prisme droit dont toutes les faces sont carrées donc égales et superposables. Le cube figure parmi les solides les plus remarquables de l'espace. C'est le seul des cinq solides de Platon ayant exactement 6 faces, 12 arêtes et 8 sommets. Son autre nom est « hexaèdre régulier ». Le cube est un zonoèdre à trois générateurs.
| Cube | |
| |
| Type | Solide platonicien |
|---|---|
| Faces | 6 carrés |
| Arêtes | 12 |
| Sommets | 8 |
| Faces/sommet | 3 |
| Caractéristique | 2 |
| Symbole de Schläfli | {4,3} |
| Symbole de Wythoff | 3 | 2 4 |
| Diagramme de Coxeter-Dynkin | |
| Dual | Octaèdre régulier |
| Groupe de symétrie | Oh |
| Volume | a³ |
| Aire | 6a² |
| Angle dièdre | 90° |
| Propriétés | zonoèdre convexe |
Comme il a quatre sommets par face et trois faces par sommet, son symbole de Schläfli est {4,3}.
L'étymologie du mot cube est grecque ; cube provient de kubos, le dé.
Le terme de cube, appliqué à un nombre, désigne la valeur obtenue en multipliant ce nombre par lui-même et en remultipliant le résultat par le nombre initial. Cette expression s'est imposée durant la période où l'algèbre géométrique était omniprésente, le carré d'un nombre était vu comme la surface d'un carré de côté le nombre initial et le cube d'un nombre comme le volume d'un cube de côté le nombre initial. L'expression « a3 » peut se lire « a au cube » et « a cube ».
Le 1-squelette du cube — l'ensemble de ses sommets reliés par ses arêtes — forme un graphe appelé graphe hexaédrique.
Géométrie

Le cube est un des cinq solides de Platon. Un cube appartient à la famille des prismes droits. Il possède 8 sommets et 12 arêtes. Pour sommets, on peut prendre par exemple les points de de coordonnées . De plus :
- Deux arêtes ayant une extrémité commune sont orthogonales.
- Les faces opposées sont parallèles. Les faces adjacentes sont perpendiculaires
- Tous les angles dièdres sont droits.
- Les diagonales s'intersectent en un unique point, le centre de symétrie du cube, l'isobarycentre des huit sommets.
Mais par définition ses arêtes sont toutes de longueur égale, disons a. Ses faces sont donc des carrés d'aire a2.
- L'aire du cube vaut donc 6a2 ;
- son volume vaut a3 ;
- la longueur d'une diagonale vaut a√3 ;
- la sphère circonscrite a donc pour rayon a√3/2 ;
- la sphère tangente aux arêtes a pour rayon a/√2 ;
- la sphère inscrite a pour rayon a/2 ;
- l'angle entre la diagonale et chacune des arêtes adjacentes vaut
- l'angle entre la diagonale et chacun des plans adjacents vaut
C'est l'expression de son volume qui a conduit à l'utilisation du mot cube en algèbre.
Autres définitions
Il existe d'autres définitions équivalentes du cube :
- les cubes sont les seuls polyèdres dont toutes les faces sont carrées ;
- le cube est un antidiamant d'ordre 3 à sommets réguliers et angles dièdres égaux.
Groupe des isométries
Le groupe des isométries du cube, noté Oh, et le sous-groupe de ses isométries positives (ses rotations), noté O, sont aussi appelés groupes de symétrie octaédrique, parce que ce sont les mêmes que ceux de son polyèdre dual, l'octaèdre régulier.
Le cube est l'un des polyèdres offrant le plus de symétries :
- 3 axes de rotation d'ordre 4 : axes passant par le centre de deux faces opposées ;
- 6 axes de rotations d'ordre 2 : axes passant par le milieu de deux arêtes opposées ;
- 4 axes de rotation d'ordre 3 : axes passant par deux sommets opposés ;
- la symétrie centrale par rapport au centre du cube ;
- 9 plans de symétrie : 3 plans médiateurs des arêtes, 6 plans passant par deux arêtes opposées.
Une isométrie du cube fixe son centre. Elle est donc entièrement définie par l'image d'un sommet A et de deux (B et C) de ses trois voisins (puisque ces trois points forment, avec le centre, un repère de l'espace). Le sommet A peut avoir pour image l'un quelconque, A', des 8 sommets du cube. Pour le sommet B, il y a alors 3 images possibles, parmi les trois voisins de A' puis, pour l'image de C, 2 images parmi les deux voisins restants. Ceci prouve que les isométries laissant le cube globalement invariant sont au nombre de 8 × 3 × 2 = 48, dont 24 rotations, une seule des deux images de C donnant la même orientation de A'B'C' par rapport à ABC. Les 24 rotations sont :
- l'application identité, qui est une rotation (d'angle nul et d'axe quelconque) ;
- 3 demi-tours d'axe passant par le centre de deux faces opposées (3 axes possibles) ;
- 6 quart de tours d'axe passant par le centre de deux faces opposées (3 axes possibles et 2 angles possibles) ;
- 6 demi-tours d'axe passant par les milieux de deux arêtes opposées (6 axes possibles) ;
- 8 tiers de tours d'axe passant par deux sommets opposés (4 axes possibles et 2 angles possibles).
Le groupe O de ces 24 rotations est isomorphe au groupe symétrique S4. Une rotation quelconque permute en effet les quatre diagonales du cube, et inversement, une permutation quelconque des quatre diagonales définit une unique rotation.
Les isométries négatives du cube sont les antirotations composées de ces rotations par la symétrie centrale et commutent avec elle. Le groupe Oh est donc le produit direct interne du sous-groupe O par le sous-groupe cyclique d'ordre 2 engendré par la symétrie centrale. C'est le plus gros des 7 groupes orthogonaux de réseaux de dimension 3.
Les 24 isométries négatives sont respectivement :
- la symétrie centrale
- 3 symétries par rapport à un plan passant par le centre du cube et parallèle à une face (3 plans possibles) ;
- 6 composées des symétries précédentes avec un quart de tour d'axe perpendiculaire au plan de symétrie (3 plans possibles et 2 angles possibles) ;
- 6 symétries par rapport à un plan passant par deux arêtes opposées (6 plans possibles) ;
- 8 composées d'un sixième de tour d'axe passant par deux sommets opposés avec la symétrie par rapport au plan passant par le centre du cube et perpendiculaire à cet axe (4 axes possibles et 2 angles possibles). Le plan de symétrie intersecte les arêtes du cube en formant un hexagone régulier.
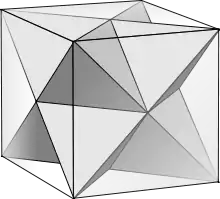
Enfin, les huit sommets du cube peuvent se répartir en deux tétraèdres réguliers, symétriques l'un de l'autre par la symétrie centrale. Il en résulte que, sur les 48 isométries du cube, 24 laissent chacun de ces tétraèdres invariant, et 24 échangent les deux tétraèdres. Les 24 isométries du cube laissant les tétraèdres invariants forment le groupe des isométries du tétraèdre : 12 sont des rotations, et 12 des isométries indirectes. Ces 24 isométries permutent les quatre sommets du tétraèdre.
Patrons
Il existe onze patrons du cube ; en voici quatre :
 Développement en croix, les carrés latéraux peuvent être placés plus bas ou plus haut
Développement en croix, les carrés latéraux peuvent être placés plus bas ou plus haut Développement en zigzag
Développement en zigzag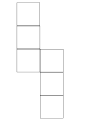 Ce développement tient dans un rectangle de deux sur cinq et minimise l'espace perdu
Ce développement tient dans un rectangle de deux sur cinq et minimise l'espace perdu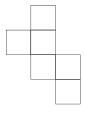 Le carré de gauche peut être placé plus bas ou plus haut
Le carré de gauche peut être placé plus bas ou plus haut
Sections
Un plan et un cube peuvent se rencontrer ou non. S'ils se rencontrent, leur intersection peut dessiner[1]
- un point
- un segment
- un triangle
- un quadrilatère, au moins trapèze, parfois un rectangle ou même un losange[2].
- un pentagone. Ce pentagone possède toujours deux paires de côtés parallèles
- un hexagone possédant trois paires de côtés parallèles
Le cube n'ayant que six faces, il n'est pas possible d'obtenir de section ayant plus de 6 côtés.
 Section suivant un triangle
Section suivant un triangle Section suivant un trapèze
Section suivant un trapèze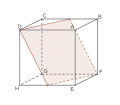 Section suivant un losange
Section suivant un losange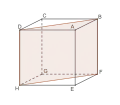 Section suivant un rectangle d'aire maximale
Section suivant un rectangle d'aire maximale Section suivant un pentagone possédant deux paires de côtés parallèles
Section suivant un pentagone possédant deux paires de côtés parallèles Section suivant un hexagone possédant trois paires de côtés parallèles
Section suivant un hexagone possédant trois paires de côtés parallèles
L'intersection d'un plan et d'un cube peut donner trois types de polygones réguliers:
- le triangle équilatéral, pour les plans perpendiculaires à une diagonale et dont la distance à une extrémité de la diagonale est inférieure au tiers de la longueur de celle-ci. Grâce à la section du cube ABCDEFGH par le plan DBE (voir illustration ci-dessous) qui est un triangle équilatéral DBE de centre Ω, on obtient que la diagonale [AG] du cube est divisée en deux parties [GΩ] et [ΩA] dans le ratio 2:1. On obtient en outre que le cube est composé de trois solides de même hauteur: deux pyramides ADBE et GCHF, et le solide CHFDEB;
- le carré, pour les plans parallèles à une des faces. Mais on peut aussi obtenir un carré en coupant le cube par un plan parallèle à un plan diagonal et à une distance de celui-ci;
- l'hexagone régulier, en coupant le cube par le plan médiateur d'une de ses diagonales.
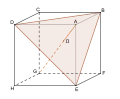 Diagonale du cube décomposée en deux parties dans le ratio 2:1 par une section en triangle équilatéral
Diagonale du cube décomposée en deux parties dans le ratio 2:1 par une section en triangle équilatéral Section du cube selon un carré. Les sommets supérieurs sont à une distance de A égale à la moitié de AC
Section du cube selon un carré. Les sommets supérieurs sont à une distance de A égale à la moitié de AC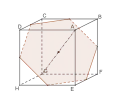 Section hexagonale du cube par le plan médiateur de [AG}
Section hexagonale du cube par le plan médiateur de [AG}
Il n'est pas possible d'obtenir un pentagone régulier[1] car, la section ayant 5 côtés, le plan coupe nécessairement deux faces opposées du cube, la figure possède donc deux côtés parallèles, ce qui n'arrive pas dans le pentagone régulier. Il n'est pas possible d'obtenir une section sous forme de triangle rectangle[1] car tous les angles du triangle obtenu par section sont aigus. Il n'est pas possible d'obtenir de section qui soit un trapèze rectangle sans être un rectangle.
L'aire maximale d'une section du cube de côté a est[3] . Cette aire est obtenue par la section suivant un plan contenant deux arêtes opposées du cube.
Le cube et les autres polyèdres
Le dual du cube est l'octaèdre régulier. Ce qui explique que les deux solides possèdent le même groupe d'isométries.
Le cube s'inscrit dans un dodécaèdre régulier : les sommets du cube sont des sommets du dodécaèdre et les arêtes du cube sont formées de segments joignant deux sommets non consécutifs dans une face pentagonale du dodécaèdre. Il y a ainsi cinq façons d'inscrire un cube dans un dodécaèdre régulier.
On peut aussi inscrire le cube dans un dodécaèdre rhombique. Les sommets du cube correspondent aux sommets d'ordre 3 du dodécaèdre rhombique et les arêtes du cube correspondent aux diagonales des losanges.
Fascination du cube
Le cube a joué un rôle important dans la géométrie et la cosmologie grecque. Platon le classe comme le quatrième solide, le premier construit à l'aide de triangles isocèles rectangles :
« Groupés par quatre avec leurs angles droits se rencontrant au centre, ces triangles isocèles forment un quadrangle. Six de ces quadrangles en s'accollant ont donné naissance à huit angles solides, composés chacun de trois angles plans droits et la figure obtenue est un cube (Timée, 54c - 55 d) »
Comme chaque solide de Platon, le cube est associé à un élément. Comme élément le plus stable, il est associé à la Terre.
Dans une autre clé symbolique, il symbolise le monde matériel et l'ensemble des quatre éléments. Symbole de stabilité, il se trouve souvent à la base des trônes[4].
Le cube a été l'objet d'un problème qui s'est révélé insoluble : la duplication du cube à la règle et au compas.
Dans la cosmologie de Kepler, le cube est associé à la planète Saturne.
On retrouve aussi le cube dans la symbolique franc-maçonne. Le cube y symbolise les progrès que doit faire le compagnon pour passer de la pierre brute au solide parfait.
Cube fait partie d'une séquence de trois films canadiens. Apple a produit l'ordinateur Cube, Nintendo la console GameCube. Le Rubik's Cube est un casse-tête dont la réflexion se base sur des associations de couleur. Comprendre sa solution fait appel à un groupe de permutations.
On retrouve un cube tronqué dans le tableau Melencolia d'Albrecht Dürer. L'Atomium de Bruxelles est un cube. En effet, le cube est un des réseaux possibles en cristallographie pour l'argent, l'or, le cuivre, le platine, le diamant, le sel, entre autres.
Notes et références
- Gérard Villemin, « Section du cube » (consulté le ).
- IREM de Paris Nord, « Section du cubes et de pyramide » (consulté le ).
- Chuanming Zong, « What is known about unit cubes », Bulletin of the amarican mathematical society, vol. 42, no 2, (lire en ligne), p. 5
- Jean Chevalier et Alain Gheerbrant, Dictionnaire des symboles, Laffont, , p. 328.
Voir aussi
Articles connexes
Lien externe
Matthieu Aubry, « Le chemin le plus court sur le cube », sur matthieu.net





