Dé
Un dé est un objet, généralement de petite taille et de forme cubique, qui permet de tirer aléatoirement un nombre ou un symbole parmi plusieurs possibilités.


Dés ordinaires

.jpg.webp)
Les dés les plus courants sont des petits cubes de 1 à 2 cm de côté (16 mm étant le standard), possédant donc 6 faces numérotées de 1 à 6, généralement à l’aide de motifs de points. Traditionnellement, la somme des nombres situés sur deux faces opposées est égale à 7 ; par conséquent, les faces numérotées 1, 2 et 3 se touchent en un sommet du dé. Deux choix sont donc possibles : placer ces faces dans le sens des aiguilles d’une montre ou dans l’autre sens autour de ce sommet.
Les arêtes possèdent un biseau arrondi, pour qu’il roule plus facilement (ce qui fait que la forme exacte d'un dé n'est pas tout à fait un cube mais plutôt une sphère tronquée). Le problème des biseaux se situe au niveau des coins car ceux-ci peuvent s’avérer trop arrondis. Il arrive quelquefois qu’un dé à 6 faces s’arrête sur un de ses coins s’il est lancé sur une nappe en dentelle, ou en étoffe suffisamment molle.
Les dés sont jetés afin de fournir des nombres aléatoires, généralement pour les jeux de hasard, et sont donc un exemple de générateur de nombres aléatoires. Cependant, comme les numéros sont d’ordinaire figurés à l’aide de trous, certaines faces se voient retirer plus de matériau que d’autres, ce qui provoque un léger biais statistique. Ce biais peut être réduit, comme dans le cas des dés asiatiques où la face numérotée 1 possède un trou largement plus grand que les autres, ou dans le cas des dés utilisés dans les casinos où les trous sont remplis avec de la peinture de même densité que le matériau utilisé[1].

Du point de vue pratique, les dés sont jetés, seuls ou en groupes, à la main ou à l’aide d’un récipient destiné à cet usage, sur une surface plane. La face prise en compte pour la lecture de la valeur de chaque dé est celle qui est située sur le dessus lorsqu’il s’arrête.
 Dés cubiques utilisé au craps (jeu d’argent dans les casinos).
Dés cubiques utilisé au craps (jeu d’argent dans les casinos).
À la différence des dés traditionnels, les points ne sont pas gravés sur les dés, mais imprimés pour respecter l'équilibre (équiprobabilité). Dés cubiques transparents.
Dés cubiques transparents. Divers dés à jouer.
Divers dés à jouer.
Histoire
Les dés tirent probablement leur origine des os des chevilles (spécifiquement l’astragale) d’animaux tels le bœuf. Il n’est pas possible de déterminer précisément l’apparition des dés et leur distinction des osselets, les écrivains antiques semblant confondre les deux jeux. Il est certain en revanche qu’ils datent des temps préhistoriques. Leur présence dans des tombes anciennes de la vallée de l’Indus, des dés cubiques vieux de 4 300 ans y ont été retrouvés[2], semble pointer vers une origine asiatique. À cette époque, la somme de faces opposées ne vaut pas encore systématiquement 7[2]. Le jeu de dé est mentionné dans le Rig-Veda et l’Atharvaveda indiens[3].
La connaissance de la numération étrusque, et plus précisément la forme écrite de leurs 6 premiers chiffres, s’est effectuée en découvrant des dés[4] à jouer (ou à divination) dans les objets familiers accompagnant le mort dans sa tombe.
Les jeux de dés furent populaires ensuite à Rome, particulièrement pendant les jours fastes de l’Empire romain, bien qu’ils fussent interdits, sauf pendant les Saturnales. Horace décrivit par exemple ce qu’il présentait comme un jeune homme typique de l’époque, qui perdait son temps aux dés plutôt qu’à dompter son cheval. Jouer de l’argent aux dés était le sujet de plusieurs lois spécifiques ; l’une d’elles statuait qu’aucun procès ne pouvait être demandé par une personne qui autorisait les paris dans sa maison, même s’il avait été attaqué ou si on avait triché contre lui. Les joueurs professionnels étaient cependant courants et certains de leurs dés pipés ont été préservés.
Le Musée Saint-Raymond des Antiques de Toulouse expose dans une vitrine un dé romain en os : il porte les chiffres 4, 5 et 6, chacun répété deux fois. On ignore à quel jeu il servait.
Tacite rapporte que les tribus germaniques adoraient particulièrement les dés et étaient prêtes à mettre en jeu leur propre liberté après avoir perdu tout le reste. Plusieurs siècles plus tard, les dés devinrent le passe-temps des chevaliers et des écoles, et des guildes de dés existèrent. Au Moyen Âge le terme "décier", désigne le métier de fabricant de dés[5].
En Inde, les dés étaient utilisés notamment pour jouer à partir du XIe siècle une version du jeu d'échecs appelée chaturaji (en) parfois confondue avec le Chaturanga, un des ancêtres du jeu d’échecs. Le chaturaji (en) aurait été joué à cette époque par quatre joueurs avec des dés à 8 faces marquées 2, 3, 4 et 5, chacun indiquant un des types de pièces du jeu comme devant être jouée ce tour[6]. On a d’ailleurs retrouvé en France des jeux d’échecs proche du Chaturanga, datant de l’époque romane et se jouant également avec des dés, où le roi présentait les attributs de Charlemagne.
Dans de nombreux pays asiatiques, les dés sont depuis toujours un passe-temps populaire.

 Collection de dés anciens originaires d’Asie.
Collection de dés anciens originaires d’Asie._with_faces_inscribed_with_Greek_letters_MET_10.130.1158_001.jpg.webp)
.jpg.webp)
 Dé de la Rome antique.
Dé de la Rome antique. Dé toupie à six faces.
Dé toupie à six faces.
Variantes
Dés non cubiques


Certains dés ont la forme d’un polyèdre autre que le cube. Jadis peu employés dans le jeu, ils sont devenus plus populaires depuis les années 1950, particulièrement après l’introduction des wargames, jeux de rôle, jeux de cartes à collectionner et de certains jeux de société. Ces dés sont généralement en plastique et leurs faces portent des nombres plutôt que des motifs de points.
S’il s’agit d’une nouveauté aux temps modernes, il semble que certaines cultures anciennes en ont utilisé (en particulier, deux dés icosaédriques datant de la Rome antique sont exposés au British Museum de Londres).
Les solides platoniciens sont utilisés de façon courante pour les dés à 4, 6, 8, 12 et 20 faces. D’autres formes peuvent être trouvées pour des dés à 2, 3, 5, 7, 10, 14, 16, 18, 24, 26, 28, 30, 32, 34, 36, 50, 60, 100 ou 120 faces, mais à part le dé à 10 faces, ils sont peu utilisés, à cause de leur rareté et aussi parce que la lecture du nombre devient difficile, les faces étant presque sur le même plan et la verticalité peu visible.
Un grand nombre de distributions de probabilités différentes peuvent être obtenues à l’aide de ces dés. Par exemple, deux dés à 10 faces peuvent être utilisés pour produire un nombre compris entre 1 et 100 (l’un des dés donnant le chiffre des dizaines, l’autre celui des unités, le tirage « 00 » correspondant à 100 ou 0 suivant le jeu pratiqué) afin d’obtenir une distribution linéaire de pourcentages. En additionnant les résultats de plusieurs dés, il est possible d’approcher une distribution normale ; en éliminant les tirages les plus (ou les moins) élevés, de modifier ces distributions, etc. à l’aide de ces techniques, les jeux peuvent approcher avec suffisamment de variété les probabilités des événements qu’ils simulent.
L’équiprobabilité de ces dés (c’est-à-dire la probabilité égale d’obtenir n’importe laquelle de ses faces) est sujette à controverse ; les dés à 6 faces utilisés dans les casinos ont l’obligation légale d’être équiprobables. Les procédés de fabrication utilisés pour les autres types de dés n’ont aucune obligation de ce genre.
Des dés sphériques existent aussi. Leur fonction est identique à celle des dés à 6 faces, mais ils possèdent une cavité interne octaédrique dans laquelle un poids se déplace et provoque leur arrêt dans une direction parmi six. Ils nécessitent cependant une surface plane et horizontale pour fonctionner correctement.
Dés non cubiques courants
.jpg.webp)
Les formes les plus couramment utilisées, en dehors des dés cubiques à 6 faces, sont :
- le tétraèdre, un dé à 4 faces. Ces dés ne roulant quasiment pas, ils comportent trois nombres sur chaque face, chacun inscrit le long d’une arête, arrangés de telle façon que celui situé soit sur l’arête du bas soit sur le sommet des trois faces visibles soit le même ; ce nombre est celui pris en compte lors d’un lancer.
- l’octaèdre, un dé à 8 faces. Chaque face est triangulaire. La somme des faces opposées est généralement égale à 9.
- le trapézoèdre pentagonal, un dé à 10 faces. Le seul dé courant qui ne soit pas un solide platonicien. Il est utilisé le plus souvent par paire pour générer les nombres de 0 à 99, l’un figurant les dizaines (00, 10, 20… jusqu’à 90), l’autre les unités (de 0 à 9). La position des faces 00 et 0 représente 0 ou 100 selon le jeu.
- le dodécaèdre régulier, un dé à 12 faces. Chaque face est un pentagone régulier.
- l’icosaèdre, un dé à 20 faces.
Dans le domaine des wargames et des jeux de rôle, les dés sont notés en mettant le nombre de faces après : d4 (dé à quatre faces), d6, d8, d10, d12, d20 et d100 (ou d%, sous la forme de deux d10) sont les plus utilisés.
Dés particuliers
Il existe aussi des formes plus rares de dés non cubiques.
- 1 face : sphère où sont inscrits les chiffres de 1 à 6.
- 2 faces : cylindre. Il s’agit ni plus ni moins d’une pièce de monnaie possédant un 1 sur une face et un 2 sur l’autre. Lorsqu’un tel tirage est nécessaire, le tirage à pile ou face est traditionnellement employé.
- 3 faces : prisme triangulaire tronqué et arrondi, il est souvent remplacé par un dé à 6 faces dont le résultat est divisé par 2, arrondi à l’entier supérieur.
- 5 faces : prisme triangulaire.

- 7 faces : prisme pentagonal.
- 14 faces : bipyramide heptagonale.
- 16 faces : bipyramide octogonale.
- 24 faces : tétrakihexaèdre.
- 30 faces : triacontaèdre rhombique.
- 34 faces : heptadecagonal trapezohedron.
- 37 faces, pour remplacer une roulette de casino.
- 50 faces : bipyramide icosakaipentagonale.
- 60 faces : pentakidodécaèdre ou hexacontaèdre trapézoïdal.
- 100 faces : zocchièdre.
- 120 faces : hexaki icosaèdre.
 Dé à 2 faces (cylindre).
Dé à 2 faces (cylindre). Dé à 3 faces.
Dé à 3 faces. Dé à 5 faces.
Dé à 5 faces. Dé à 6 faces sphérique.
Dé à 6 faces sphérique. Dé 6 sphérique ouvert, montrant son mécanisme.
Dé 6 sphérique ouvert, montrant son mécanisme. Dé à 30 faces.
Dé à 30 faces. Dé à 34 faces.
Dé à 34 faces. Dé à 50 faces.
Dé à 50 faces. Dé à 60 faces.
Dé à 60 faces. Dé à 100 faces sphérique ou zocchièdre, ici de la marque Zocchihedron.
Dé à 100 faces sphérique ou zocchièdre, ici de la marque Zocchihedron. Dé à 120 faces.
Dé à 120 faces.
Numérotation
La plupart des faces des dés sont numérotées par une suite ininterrompue de nombres entiers, débutant par un (ou zéro), exprimés par des trous ou des chiffres. Des exceptions existent cependant :
- dé doubleur ou videau, utilisé entre autres au backgammon, portant les nombres 2, 4, 8, 16, 32 et 64 et symbolisant le coefficient multiplicatif actuel de la mise initiale. Ce dé n’est pas jeté et sert simplement à noter l’enjeu.
- dés pour le jeu de Poker d'as où les figures des cartes à jouer sont représentées : as, roi, dame, valet, dix et neuf.
- dé spécifique pour jouer au Mah-jong.
- dés colorés, chaque face portant une couleur différente.
- dés comportant des dessins sur les faces, utilisés par exemple pour déterminer certaines occurrences de jeux de figurines ou des positions dans un jeu érotique.
- dans le jeu de plateau Formule Dé, les dés représentent les vitesses de la voiture : leurs chiffres de départ vont croissant, de sorte qu’il faut beaucoup de chance pour doubler une voiture en 3e vitesse avec le dé de la 2e vitesse.
- les dés à 10 faces officiels du jeu Vampire : la Mascarade comportent une ankh au lieu du 1, pour rappeler la « vie éternelle » des vampires. Les dés de la première édition étaient assortis à la couverture du livre de base : verts, mouchetés gris et noir, avec une rose rose à la place du 1.
- les dés à 6 faces employés dans les trois extensions du jeu de plateau Talisman (3e édition) sont numérotés ainsi : 1, 1, 2, 2, 3, 4
- les dés à 20 faces compteur de points de vie de Magic: The Gathering ont le symbole de l'extension d’où provient le dés à la place du chiffre 20, et ont la particularité d'avoir leurs valeurs adjacentes qui se suivent
 Dé videau employé au backgammon.
Dé videau employé au backgammon. Dés « Fudge » issus du jeu de rôle Fudge.
Dés « Fudge » issus du jeu de rôle Fudge. Dés mathématiques.
Dés mathématiques. Dés chinois.
Dés chinois.
Probabilités
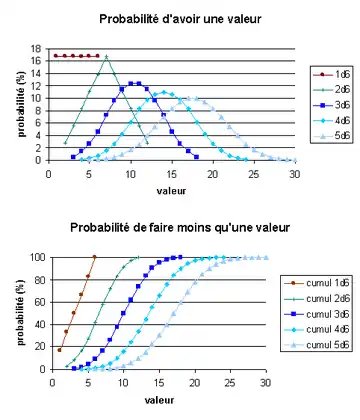
Méthode
Pour un simple lancer d’un seul dé à 6 faces équilibré, la probabilité d’obtenir n’importe quelle valeur 1 à 6 est exactement de 1⁄6. Le tirage suit donc une loi uniforme discrète. Le tirage de n dés suit une loi multinomiale dont les probabilités p1, p2, …, p6 sont toutes égales à 1⁄6, si le dé n’est pas pipé.
Si on jette deux dés et qu’on additionne les nombres obtenus sur les deux faces supérieures, les tirages ne sont plus distribués de façon uniforme mais suivent une distribution triangulaire :
| Total des dés | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probabilité | 1⁄36 | 2⁄36 | 3⁄36 | 4⁄36 | 5⁄36 | 6⁄36 | 5⁄36 | 4⁄36 | 3⁄36 | 2⁄36 | 1⁄36 |
Le tirage le plus probable est alors 7.
Avec trois dés ou plus, la distribution se rapproche d’une distribution normale avec l’ajout de chaque dé (conséquence du théorème central limite). La distribution de probabilité exacte Fi pour un nombre de dés peut être calculée par convolution répétée de la distribution de probabilité d’un dé simple avec elle-même :
- Fi(m ) = ∑n F1(n ) Fi-1(m - n ).
En s’inspirant de la toupie Sevivon, il est possible de construire des générateurs aléatoires de n’importe quelle valeur.
Déterminer si un dé est « pipé »
Un dé est dit « pipé » si la loi n’est plus uniforme. Lorsque c’est intentionnel, on s’arrange pour qu’un résultat sorte plus fréquemment, ou au contraire moins fréquemment, les autres faces ayant la même probabilité d’apparition entre elles. S’il s’agit d’un défaut non intentionnel, chaque face va avoir une probabilité propre.
Si l’on jette le dé plusieurs fois de suite, on ne va pas obtenir une alternance stricte de valeurs. Par exemple, si l’on tire un dé deux fois de suite, on a 6 chances sur 36, soit 16,66… % de chances, d’obtenir deux fois le même résultat (chaque doublon a 1⁄36 chances d’apparaître, et il y a 6 doublons) ; dans un cas sur six, on obtient deux fois le même lancer. La fréquence observée pour chaque événement va se voir s’approcher de la fréquence théorique sur un grand nombre de lancer, par exemple 100.
Si l’on fait n lancers, pour savoir si le dé est équilibré (c’est-à-dire si l’on a effectivement 1⁄6 de chances d’avoir chaque figure), il faut utiliser un test du χ² d’adéquation à cinq degrés de liberté (puisqu’il y a six résultats mais que leurs probabilités sont complémentaires). Le nombre de lancers minimal est de 30 (5 divisé par la fréquence théorique, 1⁄6 = 0,166…, cf. Test du χ² > Conditions du test). Si l’on appelle Oi le nombre de lancers donnant le chiffre i, on a le tableau de résultats suivant :
| Résultat | Nombre d’occurrences |
|---|---|
| 1 | O1 |
| 2 | O2 |
| 3 | O3 |
| 4 | O4 |
| 5 | O5 |
| 6 | O6 |
avec ∑i Oi = n
Le χ² est
| Fiabilité (p) |
99 % (p = 0,99) |
95 % (p = 0,95) |
90 % (p = 0,9) |
50 % (p = 0,5) |
10 % (p = 0,1) |
5 % (p = 0,05) |
1 % (p = 0,01) |
0,1 % (p = 0,001) |
|---|---|---|---|---|---|---|---|---|
| χ² | 0,55 | 1,15 | 1,61 | 4,35 | 9,24 | 11,07 | 15,09 | 20,52 |
Par exemple, si on fait un tirage avec un dé équilibré, le χ² est supérieur ou égal à 0,55 avec une probabilité de 0,99. Il est supérieur ou égal à 15,09 avec une probabilité de 0,01.
Expressions liées au dé

- « Les dés sont jetés », traduction littérale du latin alea jacta est (aussi traduite par « le sort en est jeté »)[alpha 1], phrase prononcée par Jules César après qu’il eut franchi le Rubicon.
- Cette phrase signifie qu’on a fait une action irréversible, et que l’avenir est entre les mains du hasard.
- « Un coup de dé », représente le hasard.
- Voici un exemple : cette opération s’est jouée sur un coup de dé. Cette phrase signifie qu’une partie importante de ladite opération s’est accomplie par la chance, par le hasard.
- Un autre exemple est la fameuse phrase de Stéphane Mallarmé : « Un coup de dé jamais n’abolira le hasard. »
- « Dieu ne joue pas aux dés » d’Albert Einstein lors de sa confrontation avec la physique quantique.
- Signifiant par là son sentiment (et ce pour quoi il va passer le reste de sa vie) d’un Univers prédictible.
- Ce qu’il expliquera également en disant que si l’on n'est pas capable d’appréhender l’ensemble de l’Univers, c’est tout simplement que l’on ne possède pas encore la totalité des lois qui régissent cet Univers ; mais qu’une fois qu’on les possède, il devient alors possible, en théorie, sans prendre en compte un temps hypothétique infini de calcul, de déterminer les caractéristiques passées, présentes et à venir de n’importe quel élément composant l’Univers.
- Cette idée de prédictibilité est contredite fondamentalement par le principe d'incertitude d'Heisenberg
- « Les dés sont pipés » signifie que quelqu’un ne joue pas le jeu. Par exemple, une personne qui avait les réponses lors d’un examen : les dés étaient pipés.
Notes et références
Notes
- On traduit aussi cette expression latine par « le sort en est jeté », car en latin le mot alea avait déjà, à côté du sens propre « dé », le sens figuré de « sort ».
Références
- « Casino Dice », sur www.dice-play.com (consulté le )
- Thierry Depaulis, « Les plus vieux dés du monde », Jeux et Stratégie, no 55, , p. 45.
- 2.3, 4.38, 6.118, 7.52, 7.109
- Une paire unique de dés d’ivoire conservée à la Bibliothèque Nationale de France, Paris.
- « Les Jeux de dés au XIIIe siècle », medieval-moyen-age.net, 27 juillet 2005.
- Jean-Louis Cazaux, Guide des échecs exotiques et insolites, Chiron éditeur, 2000.
Voir aussi
Articles connexes
- Table des caractères Unicode/U2600 : les symboles 2680 à 2685 (en hexadécimal) représentent les faces des dés traditionnels
⚀ ⚁ ⚂ ⚃ ⚄ ⚅ - Jeu de dés
- Dés non-transitifs
- Dés de Sicherman
- Polyèdre
- Tour à dés
- Système sénaire
Liens externes
- (en) Dice (Wolfram MathWorld, analyse des probabilités aux dés)
- (en) Fair Dice (étude des différents polyèdres conduisant à des dés équilibrés)
- « Une collection de 150 dés de tous genres et de toutes cultures »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)

