Groupe symétrique
En mathématiques, plus particulièrement en algèbre, le groupe symétrique d'un ensemble E est le groupe des permutations de E, c'est-à-dire des bijections de E sur lui-même. N'est traité dans le présent article, à la suite de la définition générale, que le cas E fini.
Définition
Soit E un ensemble. On appelle groupe symétrique de E l'ensemble des applications bijectives de E sur E muni de la composition d'applications (la loi ∘). On le note S(E) ou (ce caractère est un S gothique).
Un cas particulier courant est le cas où E est l'ensemble fini {1, 2, … , n}, n étant un entier naturel ; on note alors ou Sn[1] le groupe symétrique de cet ensemble. Les éléments de sont appelés permutations et est appelé groupe des permutations de degré n ou groupe symétrique d'indice n (un sous-groupe du groupe symétrique est appelé un groupe de permutations).
Si deux ensembles sont équipotents alors leurs groupes symétriques sont isomorphes. En effet, si f est une bijection de E dans F, alors l'application de S(E) dans S(F) qui à σ associe f∘σ∘f−1 est un isomorphisme. En particulier si E est un ensemble fini à n éléments, alors est isomorphe à . En conséquence, il suffit de connaître les propriétés du groupe pour en déduire celles du groupe . C'est pourquoi la suite de cet article ne portera que sur .
Exemple
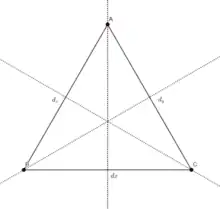
Les six isométries du groupe de symétrie d'un triangle équilatéral ABC sont les trois symétries par rapport aux médianes , et issues de respectivement les sommets A, B et C, deux rotations d'un tiers de tour dans le sens horaire ou anti-horaire et l'application identité. Elles se restreignent en six permutations des trois sommets, constituant le groupe S({A, B, C}) :
id, x = (B C), y = (A C), z = (A B), r = (A B C) et r−1 = (C B A).
La table de Cayley de ce groupe est :
| id | r | r−1 | x | y | z | |
|---|---|---|---|---|---|---|
| id | id | r | r−1 | x | y | z |
| r | r | r−1 | id | z | x | y |
| r−1 | r−1 | id | r | y | z | x |
| x | x | y | z | id | r | r−1 |
| y | y | z | x | r−1 | id | r |
| z | z | x | y | r | r−1 | id |
Origine et importance
Historiquement, l'étude du groupe des permutations des racines d'un polynôme par Évariste Galois est à l'origine du concept de groupe.
Un théorème de Cayley assure que tout groupe est isomorphe à un sous-groupe d'un groupe symétrique.
Propriétés
Générateurs du groupe symétrique
Une transposition est un 2-cycle, c'est-à-dire une permutation qui échange deux éléments et laisse les autres inchangés. On note (i, j) la transposition qui échange l'élément i avec l'élément j.
Il existe un algorithme permettant de décomposer une permutation en produit de transpositions. Ainsi l'ensemble des transpositions forme un système de générateurs de .
On peut se limiter aux transpositions de la forme τi = (i, i + 1) puisque, pour i < j, il est possible de décomposer
Ces n – 1 générateurs permettent de donner une présentation du groupe symétrique, avec les n(n + 1)2 relations[3] :
Il s'agit donc d'un cas particulier de groupe de Coxeter et même d'un groupe de réflexions (en) (ce qui, pour un groupe fini, est en fait équivalent).
Il est possible également de prendre n – 1 générateurs — les transpositions si = (i, n) pour i < n — et (n – 1)2 relations[4] :
Enfin, on peut se contenter de 2 générateurs — la transposition τ1 = (1, 2) et le cycle r = (1, 2, … , n) — et n + 1 relations[5] :
Signature
On suppose dans cette section que l'entier n est supérieur ou égal à 2.
Toute permutation se décompose en un produit de transpositions. Ce produit n'est pas unique, mais la parité du nombre de termes d'un tel produit ne dépend que de la permutation. On parle alors de permutation paire ou impaire.
La signature d'une permutation σ, notée sgn(σ) ou ε(σ), est définie par :
L'application signature est un morphisme de groupes de dans ({–1, 1}, ×). Le noyau de ce morphisme, c’est-à-dire l'ensemble des permutations paires, est appelé le groupe alterné de degré n, noté (ce caractère est un A gothique). est donc un sous-groupe normal de et le groupe quotient est isomorphe à l'image {–1, 1} du morphisme signature. Par conséquent, est d'indice 2 dans , donc d'ordre n!/2. (Ou plus concrètement : et son complémentaire dans sont de même cardinal car pour t transposition de , l'application σ ↦ t∘σ est une bijection de dans son complémentaire.)
De plus, la suite exacte courte
est scindée à droite, donc est un produit semi-direct de par le groupe cyclique à deux éléments.
Classes de conjugaison
La classe de conjugaison d'une permutation σ est l'ensemble de ses conjuguées :
Les conjuguées de σ sont les permutations dont la décomposition en produit de cycles à supports disjoints a la même structure que celle de σ : même nombre de cycles de chaque longueur[6].
- Exemple
- Si l'on considère dans les différentes classes de conjugaison, on trouve celle de l'identité, des transpositions (ab), les permutations composées de deux transpositions de supports disjoints (ab)(cd), les cycles d'ordre 3 (abc), les permutations composées d'un cycle d'ordre 3 et d'un d'ordre 2 : (abc)(de), puis les cycles d'ordres 4 : (abcd) et 5 : (abcde).
- Les permutations (1 2 3)(4 5) et (1 3 4)(2 5) sont dans la même classe de conjugaison contrairement à la permutation (1 3)(2 5).
Le nombre de classes de conjugaison est donc égal au nombre de « partages » de l'entier n, et si la décomposition d'une permutation contient k1 « 1-cycles » (les points fixes), k2 2-cycles, … , km m-cycles, alors le nombre de ses conjuguées vaut[7] :
(On voit apparaître un coefficient multinomial.)
Propriétés issues de l'étude du groupe alterné
Le résultat fondamental dans l'étude du groupe alterné est que celui-ci est un groupe simple pour n différent de 4.
D'autre part, le groupe dérivé de est [8]. Pour n ≥ 5, c'est là le seul sous-groupe distingué propre de .
est résoluble si et seulement si n ≤ 4, ce qui a d'importantes conséquences sur la résolubilité par radicaux des équations polynomiales.
Propriétés diverses
- Si n > 4, n'a aucun sous-groupe d'indice strictement compris entre 2 et n[9].
- Tout sous-groupe d'indice n de est isomorphe à [10]. Si n est différent de 6, un tel sous-groupe est forcément le stabilisateur d'un élément de {1, … , n}.
- En revanche, possède un sous-groupe d'indice 6 transitif donc sans point fixe[11].
- est complet pour tout n différent de 2 et de 6. En effet :
- le centre de est trivial si n ≠ 2 ;
- est le seul groupe symétrique dont le groupe d'automorphismes extérieurs est non trivial[12] : il est[13] d'ordre 2.
- se plonge dans , mais pas dans si n ≥ 2[14].
Notes et références
- R. Goblot, Algèbre linéaire, Paris, 2005, p. 58, utilise la notation Sn. Les auteurs anglo-saxons écrivent en général SE plutôt que et Sn plutôt que .
- La preuve standard figure dans « Permutation#Dénombrement des permutations ».
- (en) H. S. M. Coxeter et W. O. J. Moser (de), Generators and Relations for Discrete Groups, Springer, (réimpr. 2013), 3e éd. (1re éd. 1957), 164 p. (ISBN 978-3-662-21946-1, lire en ligne), p. 63 (6.22).
- Coxeter et Moser 1972, p. 64 (6.28).
- Coxeter et Moser 1972, p. 63 (6.21).
- Démontré par exemple dans .
- (en) William Fulton et Joe Harris, Representation Theory : A First Course [détail des éditions], p. 55, aperçu sur Google Livres.
- P. Tauvel, Algèbre, 2e édition, Paris, Dunod, 2010, p. 70. Voir aussi la dernière démonstration du .
- (en) G. A. Miller (en), H. F. Blichfeldt (en) et L. E. Dickson, Theory and Applications of Finite Groups, Applewood Books (en), (1re éd. 1916) (lire en ligne), p. 166-167.
- Démontré par exemple dans .
- Voir par exemple (en) Robert A. Wilson, The Finite Simple Groups, coll. « GTM » (no 251), (lire en ligne), p. 19, ou .
- Voir par exemple Wilson 2009, p. 18-19, ou les exercices corrigés 12 et 13 de .
- Wilson 2009, p. 19.
- (en) Joseph J. Rotman (en), An Introduction to the Theory of Groups [détail des éditions], p. 23, exercice 2.8.
Voir aussi
Articles connexes
- Automorphismes des groupes symétriques et alternés (en)
- Fonction de Landau
- Groupe symétrique généralisé (en)
- Groupe de tresses
- Matrice de permutation
- Permutation
- Permutation aléatoire
- Représentations du groupe symétrique
- Tableau de Young
Bibliographie
Daniel Perrin, Cours d'algèbre [détail des éditions]
























