Tableau de Young

Diagramme de Young de forme (5, 4, 1), notation anglaise

Diagramme de Young de forme (5, 4, 1), notation française

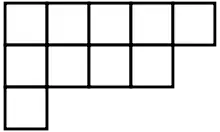
Un diagramme de Young (aussi appelé diagramme de Ferrers) est une collection finie de cases, ou cellules, organisée en lignes alignées à gauche, avec la propriété que les longueurs des lignes décroissent au sens large (chaque ligne est aussi longue ou plus longue que la précédente). La suite des longueurs des lignes donne une partition ${\displaystyle \lambda }$ de l'entier ${\displaystyle n}$ qui est le nombre total de cases du diagramme. L'image à droite montre le diagramme associé à la partition ${\displaystyle (5,4,1)}$. La partition ${\displaystyle \lambda }$ est appelée la forme du diagramme. L'inclusion d'un diagramme de Young dans un autre définit une structure de treillis connue sous le nom de treillis de Young. Si l'on énumère le nombre de cases d'un diagramme par colonnes, on obtient une autre partition, appelée la partition conjuguée ou transposée de ${\displaystyle \lambda }$.

Les cases d'un diagramme de Young sont généralement indicées par des paires d'entiers, le premier indice dénotant la ligne, le deuxième la colonne. Toutefois, il existe deux conventions pour représenter ces diagrammes, la première qui place chaque ligne en dessous de la précédente, la deuxième qui la place au-dessus. La première convention est principalement utilisée par les anglophones, la deuxième est souvent préférée par les francophones ; c'est pourquoi ces notations sont appelées notation anglaise et notation française[1]. La notation anglaise correspond aux matrices, la notation française aux coordonnées cartésiennes.

Le diagramme de Young associé à la partition 7=3+3+1 (notation française).

Un tableau de Young semi-standard de forme ${\displaystyle (3,3,1)}$ à valeurs dans ${\displaystyle [4]}$. Son poids est ${\displaystyle (1,3,1,2)}$.

Pour un entier naturel ${\displaystyle m}$, on note ${\displaystyle [m]}$ l'ensemble des entiers de ${\displaystyle 1}$ à ${\displaystyle m}$. Un tableau de Young est obtenu en remplissant les cellules d'un diagramme de Young avec des entiers. À l'origine, les entrées étaient des variables ${\displaystyle x_{1},x_{2},x_{3},\ldots }$; maintenant, on utilise des entiers. Dans leur application originale aux représentations du groupe symétrique, les tableaux de Young ont ${\displaystyle n}$ entrées distinctes, associées arbitrairement aux cellules du tableau. Un tableau de Young est standard quand les valeurs des entrées sont distinctes deux-à-deux, et sont les entiers de 1 jusqu'au nombre total de cellules, et tel que les entrées sont strictement croissantes dans les lignes et dans les colonnes. Un tableau est semi-standard quand les lignes sont croissantes au sens large, et les colonnes croissantes au sens strict, et quand tous les entiers de 1 à la valeur maximale sont présentes.

Le poids d'un tableau est une suite qui, pour chaque valeur présente dans un tableau de Young, indique le nombre de fois qu'elle y figure. Ainsi, un tableau de Young semi-standard est un tableau standard quand son poids est ${\displaystyle (1,1,\ldots ,1)}$.

Les cellules hachurées forment un diagramme de Young de forme gauche ${\displaystyle (5,4,4,1)/(4,3,2)}$, (notation française).

Tableau de Young gauche de forme ${\displaystyle (5,4,2,2)/(2,1)}$, (notation anglaise)

Une forme gauche est un couple ${\displaystyle (\lambda ,\mu )}$ de partitions tel que le diagramme de Young de la partition ${\displaystyle \lambda }$ contient le diagramme de Young de la partition ${\displaystyle \mu }$; ceci signifie que si ${\displaystyle \lambda =(\lambda _{1},\lambda _{2},\ldots )}$ et ${\displaystyle \mu =(\mu _{1},\mu _{2},\ldots )}$, alors ${\displaystyle \lambda _{i}\geq \mu _{i}}$ pour tout ${\displaystyle i}$. Une forme gauche est notée ${\displaystyle \lambda /\mu }$ ou ${\displaystyle \lambda \setminus \mu }$. Le diagramme gauche d'une forme gauche est la différence ensembliste des diagrammes de Young de ${\displaystyle \lambda }$ et de ${\displaystyle \mu }$ : il contient les cases qui sont dans le diagramme de ${\displaystyle \lambda }$ et pas dans le diagramme de ${\displaystyle \mu }$. Un tableau de Young gauche est obtenu en remplissant les cases du diagramme gauche correspondant. À nouveau, un tableau est semi-standard si les entrées sont strictement croissantes en colonne, et croissantes au sens large en ligne. Si de plus, tous les entiers de 1 au nombre de cellules apparaissent exactement une fois, le tableau est standard.

La forme gauche d'un diagramme de Young gauche ne peut pas toujours être déterminée à partir de l'ensemble de cellules du diagramme. Par exemple, si ${\displaystyle \lambda =(5,4,2,1)}$ et ${\displaystyle \mu =(5,3,2,1)}$, le diagramme gauche de forme ${\displaystyle \lambda /\mu }$ consiste en une seule cellule en position ${\displaystyle (2,4)}$. Mais cette cellule peut être obtenue d'une infinité d'autres façons, par exemple en allongeant la première ligne des deux formes, ou en ajoutant d'autres lignes identiques. De même, si un diagramme est composé de plusieurs parties non connexes, il peut être obtenue à partir de plusieurs formes différentes.

Tout tableau semi-standard gauche ${\displaystyle T}$ de forme ${\displaystyle \lambda /\mu }$ à entrées positives détermine une suite de partitions (ou de diagrammes de Young) comme suit : on commence avec ${\displaystyle \mu }$; à la ${\displaystyle i}$-ème étape, on prend comme partition celle dont le diagramme est obtenu à partir de ${\displaystyle \mu }$ en ajoutant toutes les cellules de ${\displaystyle T}$ qui contiennent une valeur ${\displaystyle \leq i}$; la partition finale est la partition ${\displaystyle \lambda }$. Toute paire consécutive de diagrammes de cette suite définit une forme gauche dont le diagramme contient au plus une entrée dans chaque colonne (parce que les entrées sont croissantes en colonne). De telles formes sont appelées bandes horizontales (horizontal strips en anglais). Cette suite de partitions détermine entièrement ${\displaystyle T}$[2].

Tableau de Young de forme (7, 6, 4, 2). Le mot correspondant est 6 845 562 233 571 112 000.

Au lieu de prendre les valeurs d'un tableau de Young dans les entiers, on les prend dans un alphabet quelconque, totalement ordonné[3]. Lorsque l'on lit successivement les lignes d'un tableau de Young semi-standard, on obtient une suite de mots croissants au sens large sur cet alphabet. Chaque mot ${\displaystyle x=x_{1}\cdots x_{r}}$ de cette suite domine le suivant ${\displaystyle y=y_{1}\cdots y_{s}}$ dans le sens que ${\displaystyle r\leq s}$ et de plus ${\displaystyle x_{i}<y_{i}}$ pour ${\displaystyle 1\leq i\leq r}$. Pour le diagramme de Young de la partition (3,3,1), les mots des lignes sont ${\displaystyle 4\,234\,122}$, et chacune domine la suivante. Le produit des mots de lignes est parfois lui-même appelé tableau[4]. Dans notre exemple, c'est le mot ${\displaystyle 4234122}$. La correspondance entre mots et tableau semi-standard est bijective : pour décoder le mot, il suffit à chaque fois de prendre le préfixe le plus long qui est croissant au sens large. Dans le tableau ci-contre de forme ${\displaystyle (7,6,4,2)}$, le mot-tableau ${\displaystyle 684556223357111444}$ se factorise en lignes dont chacune domine la suivante.

L'algorithme de Schensted est un algorithme qui permet d'insérer un entier dans un tableau semi-standard ou standard, de manière à obtenir un nouveau tableau du même type. Cet algorithme permet :

• de munir l'ensemble des tableaux d'une loi de composition interne, en insérant successivement les éléments d'un tableau dans un autre.
• d'établir une bijection entre permutations, et plus généralement suites d'entiers positifs et paires de tableaux de Young standard (resp. semi-standard) ${\displaystyle (P,Q)}$ de même forme, connue sous le nom de correspondance de Robinson-Schensted-Knuth.
• d'induire une relation d'équivalence sur l'ensemble des suites finies d'entiers positifs. Deux mots sont équivalents si dans la correspondance de Robinson-Schensted, ils ont même tableau P.

Une construction géométrique de la correspondance de Robinson-Schensted entre permutations et paires de tableaux de Young standard de même forme a été donnée par Viennot.

À partir de l'étude de cette relation d'équivalence sur les mots de longueur 3, Donald Knuth a défini des règles de réécriture sur l'ensemble des mots sur ${\displaystyle [m]}$. Ces règles de réécriture induisent également une relation d'équivalence, et Knuth a démontré qu'elle coïncide avec la relation de Schensted. Une conséquence importante de ce théorème est que la loi de composition qui découle de l'algorithme de Schensted possède toutes les propriétés requises pour donner à l'ensemble des tableaux une structure de monoïde : le monoïde plaxique.

Longueurs des équerres pour la partition de 10=5+4+1.

La formule des équerres (hook-length formula en anglais) est une formule qui permet de calculer le nombre de tableaux de Young standard de forme ${\displaystyle \lambda }$ donnée. Ce nombre est important, car le nombre de tableaux de Young standard de forme donnée est égal à la dimension de la représentation irréductible du groupe symétrique ${\displaystyle S_{n}}$ correspondant à une partition ${\displaystyle \lambda }$ de ${\displaystyle n}$.

L'équerre associée à une cellule ${\displaystyle x}$ du diagramme de Ferrers ${\displaystyle Y(\lambda )}$ de forme ${\displaystyle \lambda }$ est composé de cette cellule, et de toutes les cellules à droite et en dessous (dans la notation anglaise), respectivement à droite et au-dessus (dans la notation française) de la cellule ${\displaystyle x}$. La longueur de l'équerre ${\displaystyle h(x)}$ (en anglais hook-length) est le nombre de cellules composant l'équerre. Dans l'exemple de la partition ${\displaystyle \lambda =(5,4,1)}$, la cellule en haut à gauche a 5 cellules sur la même ligne et 3 sur la même colonne. Sa longueur d'équerre est donc 7.

On note ${\displaystyle f^{\lambda }}$ le nombre de tableaux de Young standard de forme ${\displaystyle \lambda }$, pour une partition de ${\displaystyle n}$.

La figure ci-contre donne les longueurs des équerres pour la partition ${\displaystyle \lambda =(5,4,1)}$. On obtient

${\displaystyle f^{\lambda }={\frac {10!}{7\cdot 5\cdot 4\cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot 1}}=288.}$

Il y a donc 288 tableaux de Young standard de cette forme, et la représentation irréductible du groupe symétrique S₁₀ correspondante à cette partition est donc de dimension 288.

La formule des équerres est aussi appelée le théorème de Frame-Robinson-Thrall d'après les auteurs d'une preuve[5]. Une preuve combinatoire, utilisant le jeu de taquin de Schützenberger a été donnée par Novelli, Pak et Stoyanovskii[6]. En fait, de nombreuses preuves ont été données, parmi lesquelles d'autres preuves par bijection. La preuve de Novelli, Pak et Stoyanovskii est considérée par Krattenthaler comme la plus naturelle : « The bijection presented in the paper under review must be considered as the natural hook bijection »[7]. Les livres de référence, comme Sagan 2001 ou Fulton 1997, contiennent des preuves. Une démonstration élémentaire et détaillée, par Jason Bandlow, existe en ligne[8].

Une formule proche de la formule des équerres est la suivante :

Par exemple, pour les partitions (3), (2,1) et (1,1,1) de l'entier 3, il y a respectivement 1, 2 et 1 tableau(x) de Young standard de cette forme, d'où le total 1+4+1=6=3!. Une démonstration de cette formule se fait bien au moyen des treillis de Young.

Si E est un ℂ-espace vectoriel de dimension m, et λ une partition, on définit le module de Schur E^λ comme étant le ℂ-espace vectoriel dont une base est formée par l'ensemble des tableaux de Young de forme λ et à valeur dans [m]. Sachant qu'il est possible d'identifier un tableau de Young à valeurs dans [m] à un polynôme de ℂ[X_i,j|1≤i,j≤m], il existe une action naturelle de GL(E) sur les tableaux de Young par simple multiplication matricielle. Les modules de Schur sont donc des représentations de GL(E). On peut montrer que toute représentation polynomiale irréductible de GL(E) est isomorphe à un unique module de Schur.

Les caractères des modules de Schur (en tant que représentations de GL(E)) sont des polynômes symétriques appelés polynômes de Schur, d'après le mathématicien russe Issai Schur. Les tableaux de Young fournissent un moyen élégant pour exprimer ces polynômes. Par ailleurs, il existe une règle purement combinatoire qui fait appel aux tableaux de Young, et qui permet de décomposer le produit de deux polynômes de Schur. Ceci implique en particulier que les tableaux permettent de décomposer le produit tensoriel de deux représentations irréductibles de GL(E) en somme directe de représentations irréductibles.