Treillis de Young
En mathématiques, et notamment en combinatoire, le treillis de Young est l'ensemble partiellement ordonné composé de toutes les partitions d'entiers. Cet ensemble est un treillis. Il est nommé ainsi d'après Alfred Young qui, dans une série d'articles intitulés On quantitative substitutional analysis a développé la théorie des représentations du groupe symétrique. Dans la théorie de Young, les objets appelés maintenant diagrammes de Young ou diagrammes de Ferrers et l'ordre partiels définis sur eux jouent un rôle central. Le treillis de Young occupe une place éminente en combinatoire algébrique, et est l'exemple le plus simple d'ensemble ordonné différentiel (en) au sens de Stanley 1988. Il est aussi étroitement lié à la base canonique[1] des algèbres de Lie affines.
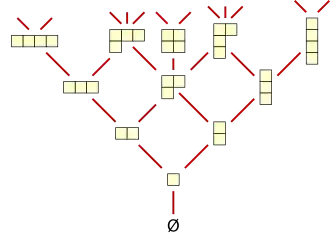
Définition
Le treillis de Young est l'ensemble partiellement ordonné formé de toutes les partitions d'entiers, ordonnées par l'inclusion de leur diagramme de Young (ou diagramme de Ferrers).
Signification
L'application traditionnelle du treillis de Young est la description des représentations irréductibles du groupe symétrique pour tout et de leurs propriétés de branchement en caractéristique zéro. Les classes d'équivalences de représentations irréductibles peuvent être paramétrées par des partitions ou diagrammes de Young. La restriction de à est sans multiplicité, et la représentation de avec partition est contenue dans la représentation de avec partition si et seulement si couvre dans le treillis de Young. En itérant cette procédure, on arrive à la base semi-canonique de Young dans la représentation de avec partition qui est indexée par les tableaux de Young standard de forme .
Propriétés
Soit l'ensemble ordonné de toutes les partitions.
- L'ensemble ordonné est un ensemble gradué : le plus petit élément est l'ensemble vide qui est l'unique partition du nombre zéro. Chaque partition a un rang. Les partitions de l'entier ont toutes rang . Ceci signifie que les rangs de deux partitions comparables sont ordonnés comme les partitions, et il existe au moins une partition intermédiaire pour tout rang intermédiaire.
- L'ensemble ordonné est un treillis. Les bornes inférieure et supérieure sont données par l’intersection et la réunion de leurs diagrammes de Young respectifs. Comme l'ensemble est un treillis dans lequel les bornes inférieures et supérieures sont représentées par des intersections et réunions, le treillis est distributif.
- Si une partition couvre[2] éléments du treillis de Young pour un certain , alors il est lui-même couvert par éléments. Les partitions couvertes par sont obtenues en supprimant une « coin » du diagramme, c'est-à-dire une cellule qui termine une ligne et une colonne. Toutes les partitions qui couvrent sont obtenues en ajoutant une cellule qui est un « coin dual » : c'est une cellule nouvelle qui est la première cellule nouvelle dans sa ligne ou et sa colonne. En fait, une telle cellule existe pour la première ligne, et pour tout autre coin dual, il existe un coin dans coin dans la ligne précédente, d'où la différence de 1 entre les partitions qui couvrent et les partitions couvertes. Par exemple, la partition (2,1,1) de l'entier 4 possède deux coins, l'un dans la première ligne et l'un dans la troisième, ce qui donne les deux partitions (1,1,1) et (2,1). La partition (2,1,1) elle-même possède trois coins duaux, dans la première, la deuxième et la quatrième ligne.
- Si deux partitions distinctes et couvrent chacune éléments de , alors ou , et et sont couvertes par éléments. Autrement dit : deux partitions ne peuvent couvrir qu'une seule même partition, car leurs diagrammes respectifs contiennent chacun exactement une cellule qui ne figure pas dans l’autre. Dans ce cas, il existe une quatrième partition qui couvre ces deux partitions et qui est la réunion de leur diagrammes.
- Les chaînes saturées (c'est-à-dire les suites de partitions dont chacune couvre la précédente) entre la partition vide et une partition sont en bijection naturelle avec les tableaux de Young standard de forme : les cellules du diagramme sont numérotées dans l'ordre dans lequel elles sont ajoutées. Plus généralement, les chaînes saturées entre et sont en bijection naturelle avec les tableaux de Young gauches de forme .
- La fonction de Möbius du treillis de Young prend les valeurs 0, +1, ou -1. Elle est donnée par la formule
Symétrie diédrale
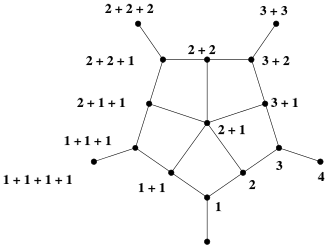
La représentation picturale usuelle du treillis de Young est un diagramme de Hasse où les éléments de même rank sont tracés à la même hauteur. Suter, en 2002[3], a montré qu'un dessin différent pouvait faire apparaître des symétries inattendues.
La partition
du e nombre triangulaire a un diagramme de Ferrers en escalier. Les plus grandes partitions contenues dans cette partition et dont le diagramme de Ferrers est un rectangle sont les suivantes :
Par exemple, pour , les éléments rectangulaires maximaux sont :
- 1 + 1 + 1 + 1
- 2 + 2 + 2
- 3 + 3
- 4
Les partitions rectangulaires ne couvrent qu'un seul élément, puisqu'elles possèdent un seul coin. Suter montre que l'ensemble des éléments en-dessous de ces partitions a non seulement une symétrie latérale à laquelle on s'attend dans le treillis de Young, mais aussi une symétrie de rotation : le groupe des rotations d'ordre agit sur cet ensemble. Comme il possède à la fois une symétrie axiale et une symétrie de rotation, il a une symétrie diédrale : le groupe diédral d'ordre opère fidèlement sur cet ensemble. La taille de cet ensemble est .
Dans le cas représenté dans la figure, c'est le groupe diédral qui opère fidèlement sur ce sous-ensemble du treillis de Young.
Formule de la somme des carrés
La considération du treillis de Young permet une démonstration simple d'une des formules étonnantes concernant les tableaux de Young, appelée parfois la « formule de la somme des carrés » (par exemple sum-of-squares formula chez Bruce Sagan[4]). Pour le diagramme de Ferrers d'une partition de donnée, notons le nombre de tableaux de Young de forme . D'après les propriétés du treillis de Young énoncées plus haut, est le nombre de chaînes de longueur de l'ensemble vide à . La formule annoncée est :
Pour établir cette formule[5], on considère l'espace vectoriel des combinaisons linéaires formelles d'éléments de , et on définit sur cet espace deux opérateurs et (pour down et up) qui correspondent à la descente et la montée dans le treillis de Young, par :
- ,
où resp. parcourt l'ensemble des éléments couverts par respectivement qui couvrent . Par exemple
et
Nous avons constaté qu'il y a un élément de plus qui couvre un diagramme donné que d'éléments couverts. Il en résulte la formule
où est l'opérateur identité. En effet, on a
- ,
où la somme est sur les éléments qui sont couverts par un élément qui couvre aussi , et est le nombre d'éléments couvrant . De même, , et en prenant la différence, on obtient la formule. Comme conséquence, on obtient pour :
- .
C'est la formule précédente pour n=1, et par récurrence on a
- .
Le nombre de chaînes de longueur reliant un élément donné à l'élément vide est . Il s'exprime par la formule
- .
Les éléments qu'on peut atteindre par des chaînes de longueur depuis l'élément vide est
- .
Il en résulte que
- .
Maintenant, on prouve que par récurrence sur . On a
- .
Ceci termine la démonstration.
Voir aussi
Notes et références
Notes
- Une base de cristal ou base canonique est une base d'une représentation telle que les générateurs d'un groupe quantique ou d'une algèbre de Lie semi-simple ont une action particulièrement simple sur elle.
- Un élément couvre un élément s'il est strictement plus grand que et qu'il n'y a pas d'élément intermédiaire entre eux.
- Suter 2002
- Sagan 2001, Chapitre 5.
- La démonstration suit Sagan 2001, p. 193-194.
Références
- Kailash C. Misra et Tetsuji Miwa, « Crystal base for the basic representation of », Communications in Mathematical Physics, vol. 134, no 1, , p. 79-88 (DOI 10.1007/BF02102090)
- Bruce Sagan, The Symmetric Group : Representations, Combinatorial Algorithms, and Symmetric Functions, New York/Berlin/Heidelberg etc., Springer, coll. « Graduate Texts in Mathematics » (no 203), , 2e éd., 238 p. (ISBN 0-387-95067-2, lire en ligne), « Section 5.1. Young's Lattice and Differential Posets »
- Richard P. Stanley, « Differential Posets », Journal of the American Mathematical Society, vol. 1, no 4, , p. 919 (DOI 10.2307/1990995)
- Ruedi Suter, « Young’s Lattice and Dihedral Symmetries », European Journal of Combinatorics, vol. 23, no 2, , p. 233-238 (DOI 10.1006/eujc.2001.0541)











![\mu (q,p)={\begin{cases}(-1)^{{|p|-|q|}}&{\text{si le diagramme gauche }}p/q{\text{ est l'union de cellules sans côté en commun}},\\[10pt]0&{\text{sinon}}.\end{cases}}](https://img.franco.wiki/i/70c4b4b1ca6925ad993f5adab7cfef7915d48a75.svg)































