Symétrie axiale
En géométrie euclidienne élémentaire, une symétrie axiale ou réflexion est une transformation géométrique du plan qui modélise un « pliage » ou un « effet miroir » : deux figures sont symétriques par rapport à une droite lorsqu'elles se superposent après pliage le long de cette droite. C'est un cas particulier de symétrie.

La symétrie axiale d'axe la droite d transforme tout point M en l'unique point M' tel que d soit la médiatrice du segment [MM']. Autrement dit : elle laisse tous les points de d invariants et transforme tout point M non situé sur d en le point M' tel que :
- la droite (MM') est perpendiculaire à l'axe de symétrie d ;
- le milieu du segment [MM'] appartient à l'axe de symétrie d.
Le point M' est alors appelé le symétrique de M par rapport à l'axe de symétrie d.
Par rapport à d, deux figures du plan sont dites symétriques lorsque l'une est l'image de l'autre par cette application, et une figure est dite symétrique lorsqu'elle est symétrique d'elle-même, c'est-à-dire globalement invariante par cette transformation. La droite d est alors dite axe de symétrie de la figure.
Propriétés
Involution
La symétrie axiale est — comme toute symétrie — une involution, c'est-à-dire qu'on retrouve le point ou la figure de départ si on l'applique deux fois. En particulier, c'est une bijection.
Conservation
La symétrie axiale est une isométrie affine ; elle conserve :
- l'alignement (la symétrique d'une droite est une droite),
- le parallélisme (les symétriques de deux droites parallèles sont parallèles),
- les distances,
- les angles géométriques (le symétrique d'un angle est un angle de même mesure),
- les périmètres (la symétrique d'une figure est une figure de même périmètre),
- les aires (la symétrique d'une figure est une figure de même aire).
Mais elle ne conserve pas l'orientation (ni, par conséquent, les angles orientés) : quand le point M tourne autour de O « dans le sens des aiguilles d'une montre », son symétrique M' tourne autour de O' dans le sens inverse.
Exemples
- Si une droite est sécante à l'axe de symétrie d en M, il en sera de même pour sa symétrique.
- Si une droite est parallèle à l'axe de symétrie d, il en sera de même pour sa symétrique.
- Si une droite est perpendiculaire à l'axe de symétrie d, elle est sa propre symétrique.
- Le symétrique par rapport à d d'un cercle de centre O est le cercle de même rayon et de centre O', le symétrique de O par rapport à d.
Construction du symétrique d'un point M par rapport à une droite d
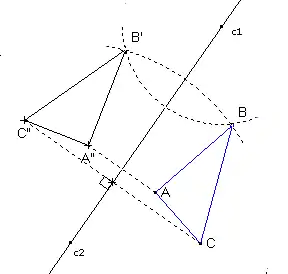
On suppose tracés un point M et une droite d ne passant pas par M.
À la règle graduée et à l'équerre
- Tracer la droite passant par M et perpendiculaire à la droite d et noter I le point d'intersection des deux droites.
- Placer sur la droite (MI) le point M' symétrique de M par rapport à la droite d tel que MI = IM'.
Au compas seul
- Placer deux points distincts A et B sur la droite d.
- Tracer l'arc de cercle de centre A et de rayon AM.
- Tracer l'arc de cercle de centre B et de rayon BM.
- Les deux arcs de cercle se recoupent en un point M' symétrique de M par rapport à d.
Notes et références
Voir aussi
Articles connexes
Liens externes
- Notice dans un dictionnaire ou une encyclopédie généraliste :