Droite sécante
En géométrie, une droite est sécante à un autre objet géométrique lorsqu'elle « coupe » cet autre objet.
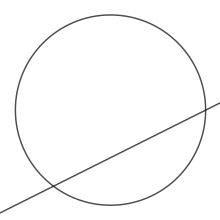
On dit que deux droites sont sécantes si elles ont un unique point commun.
Pour étudier une courbe au voisinage d'un de ses points P, il est utile de considérer les sécantes issues de P, c'est-à-dire les droites passant par P et un autre point Q de la courbe. C'est à partir de ces sécantes qu'est définie la notion de tangente à la courbe au point P : il s'agit de la limite, quand elle existe, des droites sécantes issues de P lorsque le deuxième point Q se rapproche de P le long de la courbe.
De ce fait, lorsque Q est suffisamment proche de P, la sécante peut être considérée comme une approximation de la tangente.
Dans le cas particulier de la courbe représentative d'une fonction numérique y = f(x), la pente de la tangente en un point de la courbe, est la limite de la pente des sécantes en ce point, ce qui donne une interprétation géométrique du nombre dérivé d’une fonction en un point (cf. dérivabilité).
Approximation par une sécante
Considérons la courbe d’équation y = f(x) dans un système de coordonnées cartésiennes, et considérons un point P de coordonnées (c, f(c)), et un autre point Q de coordonnées (c + Δx, f(c + Δx)). Alors la pente m de la droite sécante passant par P et Q est donnée par
Le membre de droite de l’équation précédente est le taux d'accroissement de f entre c et c + Δx. Sa limite lorsque Δx tend vers zéro, si elle existe, est appelée le nombre dérivé de f en c et notée f'(c).
Voir aussi
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Secant line » (voir la liste des auteurs).
