Limite (mathématiques)

Lorsque n est un très grand nombre (entier), son inverse ${\displaystyle {\frac {1}{n}}}$ est très proche de 0. Ce phénomène s’exprime par l’égalité ${\displaystyle \lim _{n\to \infty }{\frac {1}{n}}=0}$.

De même, on peut écrire ${\displaystyle \lim _{n\to \infty }{\sqrt {n}}=+\infty }$, car la racine carrée peut être rendue arbitrairement grande en prenant l’entier n suffisamment grand (par exemple, pour obtenir ${\displaystyle {\sqrt {n}}>1000}$, il suffit d’avoir n > 1 000 000).

A contrario, il n’existe pas de limite pour la suite périodique ${\displaystyle ((-1)^{n})_{n\in \mathbb {N} }}$, qui prend alternativement les valeurs 1 et −1, mais qui ne tend ni vers 1, ni vers −1, ni vers quoi que ce soit d’autre dans l’intervalle ]−1, 1[ ou en dehors. En tant que suite bornée, elle ne peut pas non plus tendre vers +∞ ou vers −∞.

La définition par Weierstrass de la convergence d’une suite réelle ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ vers une limite finie ${\displaystyle L\in \mathbb {R} }$ s’exprime par la formule[1]

${\displaystyle \forall \varepsilon >0\quad \exists n_{0}\in \mathbb {N} \quad \forall n\geq n_{0}\quad L-\varepsilon <x_{n}<L+\varepsilon }$

ou encore, par une formulation équivalente dans le cas des suites réelles, mais qui s’adapte au cas des suites à valeurs complexes,

${\displaystyle \forall \varepsilon >0\quad \exists n_{0}\in \mathbb {N} \quad \forall n\geq n_{0}\quad |{x_{n}-L}|<\varepsilon }$.

Cette définition s’étend encore aux suites dans un espace vectoriel normé en remplaçant la valeur absolue par la norme, et plus généralement aux suites dans un espace métrique avec la formulation

${\displaystyle \forall \varepsilon >0\quad \exists n_{0}\in \mathbb {N} \quad \forall n\geq n_{0}\quad \mathrm {d} (x_{n},L)<\varepsilon }$.

Dans chacun de ces cas, il ne peut y avoir deux limites différentes pour une même suite, ce qui permet d’exprimer la limite avec une égalité ${\displaystyle \lim _{n\to \infty }x_{n}=L}$. On trouve parfois aussi la notation ${\displaystyle x_{n}{\underset {n\to \infty }{\longrightarrow }}L}$.

On dit qu’une suite réelle ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ diverge vers +∞ dans le cas suivant :

${\displaystyle \lim _{n\to \infty }x_{n}=+\infty \iff \forall M\in \mathbb {R} \quad \exists n_{0}\in \mathbb {N} \quad \forall n\geq n_{0}\quad x_{n}>M}$.

Par analogie, elle diverge vers −∞ dans le cas

${\displaystyle \lim _{n\to \infty }x_{n}=-\infty \iff \forall M\in \mathbb {R} \quad \exists n_{0}\in \mathbb {N} \quad \forall n\geq n_{0}\quad x_{n}<M}$.

Les trois cas de limite (finie, infinie positive ou infinie négative) sont mutuellement exclusifs et ne recouvrent pas l’ensemble des suites réelles, puisque certaines n’ont pas de limite du tout. On dit alors qu’elles divergent sans limite.

Pour une suite ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ à valeurs dans un espace topologique E, on dit que la suite converge vers un élément L ∈ E si pour tout ouvert U contenant L, il existe un rang n₀ tel que pour tout n > n₀ on a x_n ∈ U. Mais l’unicité de la limite repose alors sur l’hypothèse que l’espace soit séparé.

Cette définition recouvre celles des limites de suites à valeurs réelles, complexes ou dans des espaces métriques, mais s’applique également à d’autres espaces non métrisables, comme des espaces fonctionnels non normés. Pour une même suite de fonctions, différentes normes ou topologies peuvent être prises en compte conduisant à l’existence ou non de limites (convergence simple, convergence uniforme, convergence en norme p ou au sens des distributions…)

Toute suite réelle croissante a une limite, qui est finie si et seulement si la suite est majorée. Dans ce cas, la limite de la suite est égale à la borne supérieure de ses valeurs.

De même, toute suite réelle décroissante a une limite qui est finie si et seulement si la suite est minorée, et dans ce cas la limite de la suite est égale à la borne inférieure de ses valeurs.

Ces propriétés découlent de la propriété de la borne supérieure dans l’ensemble des réels, et elles permettent de définir également la limite inférieure d’une suite minorée et la limite supérieure d’une suite majorée :

${\displaystyle \liminf x_{n}=\lim _{n_{0}\to \infty }\inf\{x_{n},n>n_{0}\}=\sup _{n_{0}\geq 0}\inf\{x_{n},n>n_{0}\}}$,

${\displaystyle \limsup x_{n}=\lim _{n_{0}\to \infty }\sup\{x_{n},n>n_{0}\}=\inf _{n_{0}\geq 0}\sup\{x_{n},n>n_{0}\}}$.

En particulier, une suite bornée converge si et seulement si sa limite inférieure est égale à sa limite supérieure, et dans ce cas la limite de la suite est cette valeur commune. Cette propriété se généralise avec l’étude des valeurs d’adhérence d’une suite à valeurs dans un espace compact.

Toute suite convergente est bornée mais une suite bornée n’est pas nécessairement convergente.

Deux suites adjacentes convergent toutes deux vers la même limite réelle.

Pour une suite ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ à valeurs réelles, complexes ou dans n’importe quel espace complet, la convergence est équivalente au critère de Cauchy :

${\displaystyle \forall \varepsilon >0\quad \exists n_{0}\in \mathbb {N} \quad \forall (n,p)\in \mathbb {N} ^{2},\quad n_{0}<n<p\Rightarrow \mathrm {d} (x_{n},x_{p})<\varepsilon }$.

Pour une suite récurrente (x_n) avec une fonction de récurrence f, si la suite converge vers un élément L en lequel la fonction f est continue, alors L est un point fixe de f.

Pour une suite ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ (à valeurs réelles complexes ou vectorielles), la série associée est aussi une suite, définie pour tout entier n ≥ 0 par ${\displaystyle S_{n}=\sum _{k=0}^{n}x_{k}}$, et si elle converge sa limite est la somme de la série, notée ${\displaystyle \sum _{k=0}^{+\infty }x_{k}}$.

La convergence de la série n’est alors possible que si la suite initiale tend vers 0. Dans le cas contraire, on dit que la série diverge grossièrement.

Dans le cas d’une suite réelle positive, la série est nécessairement croissante et admet toujours une limite finie ou infinie.

Dans le cas d’une série alternée s’écrivant ${\displaystyle S_{n}=\sum _{k=0}^{n}(-1)^{k}a_{k}}$ pour tout entier n ≥ 0, si la suite ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ est (positive) décroissante de limite nulle, la suite des termes de rang pair ${\displaystyle (S_{2p})_{p\in \mathbb {N} }}$ et la suite des termes de rang impair ${\displaystyle (S_{2p+1})_{p\in \mathbb {N} }}$ forment des suites adjacentes donc la série converge, et le reste ${\displaystyle R_{n}=\sum _{k=n+1}^{+\infty }(-1)^{k}a_{k}}$ est toujours inférieur en valeur absolue au premier terme négligé ${\displaystyle a_{n+1}}$.

Pour une fonction réelle ou complexe d’une variable réelle ou complexe, la formulation d’une limite finie en une valeur finie est semblable à celle de la limite d’une suite[2] :

${\displaystyle \lim _{x\to a}f(x)=L\iff \quad \forall \varepsilon \in \mathbb {R} _{+}^{*}\quad \exists \delta \in \mathbb {R} _{+}^{*}\quad \forall x\in {\mathcal {D}}_{f}\quad (|{x-a}|<\delta \Rightarrow |f(x)-L|<\varepsilon )}$

Cette définition moderne, cohérente avec la définition topologique générale (voir infra) et désormais en vigueur en France[3], supplante la définition historique de Weierstrass, appelée aussi « limite épointée » ou « limite par valeurs différentes »[4], enseignée encore parfois dans les universités françaises et dans d’autres pays[5] :

${\displaystyle \lim _{{x\to a} \atop {x\neq a}}f(x)=L\iff \quad \forall \varepsilon \in \mathbb {R} _{+}^{*}\quad \exists \delta \in \mathbb {R} _{+}^{*}\quad \forall x\in {\mathcal {D}}_{f}\setminus {\{a\}}\quad (|{x-a}|<\delta \Rightarrow |f(x)-L|<\varepsilon )}$.

Lorsque la fonction f est définie en un réel a, si elle admet une limite en a alors cette limite est nécessairement[6] - [7] égale à f(a). Plus précisément, la fonction admet une limite finie en un point a de son domaine de définition si et seulement si elle est continue en a. Cette condition peut aussi s’exprimer par l’égalité avec la limite épointée :

${\displaystyle f\ {\text{continue en}}\ a\iff \lim _{{x\to a} \atop {x\neq a}}f(x)=f(a)}$.

La définition de cette limite est particulièrement utile pour déterminer le nombre dérivé comme limite du taux d'accroissement.

Les limites aux bornes du domaine de la fonction inverse : ${\displaystyle \lim _{x\to -\infty }{\tfrac {1}{x}}=\lim _{x\to +\infty }{\tfrac {1}{x}}=0}$, ${\displaystyle \lim _{x\to 0^{-}}{\tfrac {1}{x}}=-\infty }$, ${\displaystyle \lim _{x\to 0^{+}}{\tfrac {1}{x}}=+\infty }$

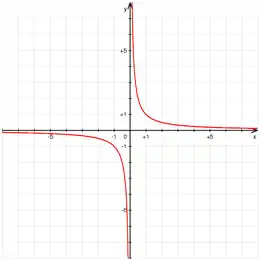
Pour une fonction f d’une variable réelle x, lorsque x se rapproche d’un réel a, il se peut que les valeurs f(x) soient très contrastées selon que la variable x soit inférieure ou supérieure à a, comme dans le cas particulier de la fonction inverse en 0, où l’on ne peut définir de limite cohérente. Dans ce cas, on peut définir une limite à gauche et une limite à droite éventuellement différentes.

La limite d’une fonction f à gauche en un réel a s’écrit ${\displaystyle \lim _{x\to a \atop x<a}f(x)}$ ou ${\displaystyle \lim _{x\to a^{-}}f(x)}$, voire f(a⁻) ou f_g(a). Sa limite à droite en a s’écrit ${\displaystyle \lim _{x\to a \atop x>a}f(x)}$ ou ${\displaystyle \lim _{x\to a^{+}}f(x)}$, voire f(a⁺) ou f_d(a).

Pour une fonction définie au voisinage à gauche et à droite d’un réel a, l’existence et l’égalité des limites à gauche et à droite est équivalente à l’existence d’une limite épointée (avec la même valeur).

Afin d’unifier les différentes formulations de limites, on recourt à la notion de voisinage, qui s’applique à tout réel (éventuellement à droite ou à gauche) et à l’infini (en +∞ ou en −∞). On utilise aussi la notation R = R ∪ {−∞, +∞} de la droite réelle achevée.

Soit f une fonction définie au voisinage[8] (éventuellement à gauche ou à droite) de a ∈ R et soit L ∈ R. On dit que la fonction f admet la limite L en a si pour tout voisinage V de L, il existe un voisinage U (à gauche ou à droite) de a tel que f(U) ⊂ V.

On démontre que le réel L de la définition, lorsqu'il existe, est unique et on l'appelle limite de f au point p. On le note :

${\displaystyle \lim _{x\to a}f(x)=L\quad {\text{ou}}\quad \lim _{a}f=L.}$

Critère séquentiel de la limite de fonction

La fonction f admet la limite L en a si et seulement si pour tout suite ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ dans ${\displaystyle {\mathcal {D}}_{f}}$ de limite a, la suite f(x_n) a pour limite L.

• La limite de x ↦ 1/x en l'infini est égale à 0 :${\displaystyle \lim _{x\to \infty }{\frac {1}{x}}=0.}$
• La limite de x ↦ 1/x en 0 n'existe pas. La limite à droite est +∞ :${\displaystyle \lim _{x\to 0+}{\frac {1}{x}}=+\infty \qquad \lim _{x\to 0-}{\frac {1}{x}}=-\infty .}$
• La limite de x ↦ x² en 3 est égale à 9 (dans ce cas la fonction est définie et continue en ce point et la valeur de la fonction est égale à la limite) :${\displaystyle \lim _{x\to 3}x^{2}=9.}$
• La limite de x ↦ x^x en 0 est égale à 1 :${\displaystyle \lim _{x\to 0}x^{x}=1.}$
• La limite de x ↦ ((a + x)² – a²)/x en 0 est égale à 2a :${\displaystyle \lim _{x\to 0}{\frac {(a+x)^{2}-a^{2}}{x}}=2a.}$
• La limite à droite de x ↦ |x|/x en 0 est égale à 1 et la limite à gauche est égale à –1 :${\displaystyle \lim _{x\to 0+}{\frac {|x|}{x}}=1,\qquad \lim _{x\to 0-}{\frac {|x|}{x}}=-1.}$
• La limite de x ↦ x sin(1/x) en +∞ est égale à 1 :${\displaystyle \lim _{x\to +\infty }x\sin {\frac {1}{x}}=1.}$
• La limite de x ↦ (cos(x) – 1)/x en 0 est égale à 0 :${\displaystyle \lim _{x\to 0}{\frac {\cos(x)-1}{x}}=0.}$

Le passage à la limite des fonctions est compatible avec les opérations algébriques :

Si

${\displaystyle \lim _{x\to p}f_{1}(x)=L_{1}\qquad {\text{et}}\qquad \lim _{x\to p}f_{2}(x)=L_{2}}$

alors

${\displaystyle \lim _{x\to p}(f_{1}(x)+f_{2}(x))=L_{1}+L_{2}\quad {\text{et}}\quad \lim _{x\to p}(f_{1}(x)\cdot f_{2}(x))=L_{1}\cdot L_{2}\quad {\text{et}}\quad \lim _{x\to p}\left({\frac {f_{1}(x)}{f_{2}(x)}}\right)={\frac {L_{1}}{L_{2}}}.}$

(La dernière propriété suppose que L₂ n'est pas nulle.)

Ces propriétés sont aussi valables pour les limites à droite et à gauche, pour le cas p = ±∞, et aussi pour les limites infinies en utilisant les règles suivantes :

• q + ∞ = ∞ pour q ≠ –∞ ;
• q × ∞ = ∞ si q > 0 ;
• q × ∞ = –∞ si q < 0 ;
• q / ∞ = 0 si q ≠ ±∞.

(Voir l'article « Droite réelle achevée ».)

Remarquons qu'il n'y a pas de règle générale pour le cas q / 0 : cela dépend de la façon dont on s'approche de 0. Certains cas, comme 0/0, 0×∞, ∞ – ∞ ou ∞/∞, ne sont pas non plus couverts par ces règles.

• Si une fonction f est positive ou nulle au voisinage de p, et si la limite de f en p existe, cette limite sera positive ou nulle.
• Si une fonction f est strictement positive au voisinage de p, et si la limite de f en p existe, cette limite sera positive ou nulle, mais on ne peut pas garantir que cette limite soit strictement positive.
• Si la limite de f en p est strictement positive (resp. négative) alors il existe un voisinage de p (épointé dans le cas de la limite épointée) dans lequel la fonction f est strictement positive (resp. négative). Par conséquent, si la limite de f en p est non nulle, il existe un voisinage de p (épointé dans le cas de la limite épointée) dans lequel la fonction ne s'annule pas.
• Si deux fonctions sont rangées dans un certain ordre au voisinage de p et si ces deux fonctions admettent des limites en p, ces limites sont rangées dans le même ordre que les fonctions.
• Théorème des gendarmes.

Il existe certaines formes de limite où il n'est pas possible de conclure directement en utilisant des opérations sur les limites, ce sont les formes dites « indéterminées » :

• 0/0 ;
• ∞/∞ ;
• ∞ – ∞ ;
• 0 × ±∞ ;
• 0⁰ ;
• +∞⁰ ;
• 1^±∞.

• Si z est un nombre complexe de module |z| < 1, alors la suite (1 ; z ; z² ; z³ ; …) de nombres complexes converge et a pour limite 0. Géométriquement, ces nombres se rapprochent de l'origine en suivant une spirale logarithmique.
• Dans l'espace métrique C([a ; b]) de toutes les fonctions continues définies sur l'intervalle [a ; b], muni de la distance de la convergence uniforme, tout élément peut être écrit comme limite d'une suite de fonctions polynomiales. C'est ce qu'affirme le théorème d'approximation de Weierstrass.

Toute sous-suite d'une suite convergente converge vers la même limite.

L'opération de passage à la limite est linéaire dans le sens suivant : si (x_n) et (y_n) sont des suites réelles convergentes et que lim x_n = L et lim y_n = P, alors la suite (x_n + y_n) est aussi convergente et a pour limite L + P. Si a est un nombre réel, alors la suite (a x_n) est convergente de limite aL. Ainsi, l'ensemble c de toutes les suites réelles convergentes est un espace vectoriel réel et l'opération de passage à la limite est une forme linéaire sur c à valeurs réelles.

Si (x_n) et (y_n) sont des suites réelles convergentes de limites respectives L et P, alors la suite (x_ny_n) est convergente de limite LP. Si ni P ni aucun des termes y_n n'est nul, alors la suite (x_n/y_n) est convergente de limite L/P.

Toute suite convergente est une suite de Cauchy et est ainsi bornée. Si (x_n) est une suite de réels, bornée et croissante (i. e. pour tout entier n, x_n ≤ x_n+1), alors elle est nécessairement convergente.

Une suite de nombres réels est convergente si et seulement si ses limites inférieure et supérieure sont finies et égales.

Toutes les notions de limite ci-dessus peuvent être unifiées et généralisées encore à des espaces topologiques M et N arbitraires : si A est une partie de M, p un élément de M adhérent à A, L un élément de N et f une application de A dans N, on dit que

• f admet L pour limite en p si pour tout voisinage V de L, il existe un voisinage W de p tel que ${\displaystyle \forall y\in W\cap A\quad f(y)\in V}$[11].

(On ne modifie pas cette caractérisation en remplaçant l'ensemble des voisinages de L (ou de p) par une base de voisinages de ce point[12], par exemple par l'ensemble des ouverts contenant ce point.)

Un espace N est séparé si et seulement si toute application f : A → N (pour tout espace M et toute partie A de M) possède, en tout point adhérent à A, au plus une limite.

La définition de limite d'une suite est un cas particulier de la définition précédente :

• Une suite ${\displaystyle (u_{n})_{n\in \mathbb {N} }}$ admet L pour limite si pour tout voisinage V de L, il existe un entier naturel N tel que ${\displaystyle \forall n\geq N\quad u_{n}\in V.}$

Si M est métrisable (ou plus généralement : héréditairement séquentiel), on dispose de la caractérisation séquentielle des limites de fonctions :

• Si M est héréditairement séquentiel alors ${\displaystyle f}$ admet ${\displaystyle L}$ pour limite en ${\displaystyle p}$ si (et seulement si) pour toute suite ${\displaystyle (x_{n})}$ dans ${\displaystyle A}$ de limite ${\displaystyle p}$, ${\displaystyle f(x_{n})\to L}$.

Si de plus N est T₁ (ou même seulement à unique limite séquentielle), ${\displaystyle f}$ admet une limite en ${\displaystyle p}$ si (et seulement si) pour toute suite ${\displaystyle (x_{n})}$ dans ${\displaystyle A}$ de limite ${\displaystyle p}$, la suite ${\displaystyle (f(x_{n}))}$ admet une limite.

D'autres généralisations de cette notion, permettant par exemple de parler de limites « à l'infini » pour un espace métrique quelconque, ou de dire qu'une intégrale est une limite de sommes de Riemann, ont été définies ; les plus puissantes utilisent la notion de filtre. On en trouvera des exemples aux divers articles traitant de convergence : convergence simple, convergence uniforme, convergence normale, convergence presque sûre, convergence en moyenne, etc.

Théorème d'interversion des limites

Christian Houzel, « Limite (notion de) », Dictionnaire de mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis et Albin Michel, Paris 1997