Espace euclidien
En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le plan ainsi que l'espace qui nous entoure. Un espace euclidien permet également de traiter les dimensions supérieures ; il est défini par la donnée d'un espace vectoriel sur le corps des réels, de dimension finie, muni d'un produit scalaire, qui permet de « mesurer » distances et angles.
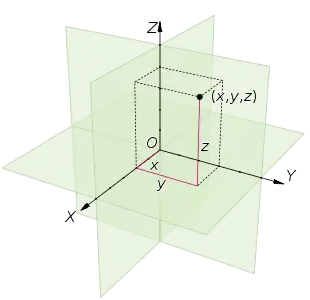
La donnée d'un produit scalaire permet par exemple de définir la notion de bases particulières dites orthonormales, d'établir une relation canonique entre l'espace et son dual, ou de préciser des familles d'endomorphismes faciles à réduire. Il permet aussi de définir une norme et par conséquent une distance donc une topologie, ce qui met à disposition les méthodes d'analyse.
Les espaces euclidiens possèdent une longue histoire ainsi que de nombreuses applications. Les relations entre cet outil et le reste des mathématiques sont multiples et variées, depuis la logique et l'algèbre jusqu'aux géométries non euclidiennes. Cet aspect est traité dans l'article « Géométrie euclidienne ».
Géométrie
Espace euclidien et bipoints
Dans le cadre de la construction des vecteurs à l'aide des classes d'équivalence de bipoints sur un espace affine, une première définition du produit scalaire peut être obtenue. La norme d'un vecteur correspond à la longueur d'un bipoint représentatif, l'angle de deux vecteurs correspond à celui de deux bipoints représentatifs de même origine. La formule donnant le produit scalaire est alors :
Dans de nombreux cas en physique classique ou en géométrie analytique, si la dimension de l'espace n'est pas trop élevée (typiquement 2 ou 3), cette définition est suffisante. Toutefois, dans le cas général, ce formalisme s'avère à la fois lourd et peu adapté pour, par exemple, l'étude des propriétés topologiques d'un espace euclidien. Une deuxième approche, purement algébrique et plus abstraite, existe, et permet d'établir plus facilement des résultats plus généraux[1].
Géométrie du triangle
Dans un espace euclidien, on peut définir — outre les distances — les angles, comme des classes d'équivalence de couples de vecteurs unitaires, deux tels couples (a, b) et (x, y) représentant le même angle s'il existe une rotation vectorielle qui envoie a sur x et b sur y.
Si E est de dimension strictement supérieure à 2, l'angle de (x, y) est toujours égal à celui de (y, x). Dans le plan, au contraire, les angles orientés forment un groupe, dans lequel les angles de (x, y) et (y, x) sont symétriques l'un de l'autre, et distincts sauf si y = ±x. On distingue alors une notion moins précise d'angle géométrique, commun à (x, y) et (y, x), et dont la mesure θ est donnée par la formule suivante :
Cette définition permet de formaliser un espace disposant de la même « géométrie du triangle », que celle fondée sur les célèbres postulats décrits les Éléments d'Euclide. Une telle géométrie vérifie les théorèmes de Thalès, de Pythagore, ou d'Al-Kashi.
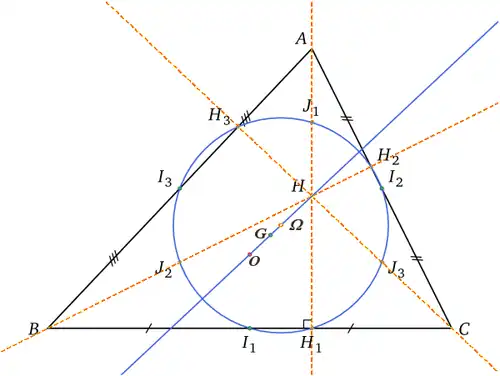
Un exemple classique est donné par le cercle d'Euler disposant de neuf points remarquables.
Formalisation et premières propriétés
Définitions
Les axiomes d'un espace vectoriel euclidien E concernent deux structures qui se combinent : la première est celle d'espace vectoriel de dimension finie sur le corps ℝ des réels ; la deuxième est la donnée d'une forme bilinéaire appelée « produit scalaire », possédant trois propriétés spécifiques (une forme bilinéaire sur E est une application de E×E dans ℝ, linéaire par rapport à chacune des deux variables).
Définitions —
- Un produit scalaire sur un espace vectoriel[2] réel[3] E est une forme bilinéaire 〈⋅, ⋅〉
- symétrique :
- définie :
- positive :
- symétrique :
- Un espace vectoriel euclidien est un espace vectoriel réel de dimension finie muni d'un produit scalaire[4].
- Un espace affine euclidien est un espace affine dont la direction est un espace vectoriel euclidien.
- La norme euclidienne, sur un espace vectoriel préhilbertien E, est la fonction de E dans ℝ+ qui à un vecteur x associe la racine carrée du produit scalaire de x par lui-même :
- La distance euclidienne associée est, entre deux vecteurs, la norme euclidienne de leur différence :
Dans le cas d'un espace affine, la distance entre deux points a et b est égale à la norme du vecteur d'extrémités a et b. Tout espace euclidien, vectoriel ou affine, est donc muni d'une structure d'espace métrique.
On dit que deux vecteurs sont orthogonaux si leur produit scalaire est nul. Le produit scalaire étant défini, il est non dégénéré : le vecteur nul est le seul vecteur orthogonal à lui-même et a fortiori le seul orthogonal à tout l'espace.
Exemples
- L'espace vectoriel ℝn, muni du produit scalaire canonique et de la norme associée, définis, pour x = (x1, … , xn) et y = (y1, … , yn), par
est un espace euclidien appelé espace euclidien canonique[5] de dimension n. - Sur l'espace vectoriel Mn(ℝ) des matrices carrées d'ordre n, identifié à ℝ(n2), le produit scalaire canonique se réécrit donc en termes de trace et de matrice transposée :
La norme associée est appelée « norme de Frobenius ». On retrouvera cette structure euclidienne sous une forme plus abstraite au § « Endomorphisme ». - L'espace vectoriel des polynômes réels de degré inférieur ou égal à n,
- muni du produit scalaire
est un espace euclidien, trivialement isomorphe à l'espace euclidien canonique de dimension n + 1. - muni d'un produit scalaire différent :
est aussi un espace euclidien. Ce produit scalaire est celui de l'espace de Hilbert L2([0, 1]) (de dimension infinie), restreint au sous-espace des fonctions polynomiales (identifiées à des polynômes) de degré inférieur ou égal à n. - muni du produit scalaire (différent des deux précédents) :
(où x0, …, xn sont n + 1 réels distincts) est isomorphe à l'espace euclidien canonique de dimension n + 1, par l'application P ↦ (P(x0), …, P(xn)).
- muni du produit scalaire
- L'espace ℂ des nombres complexes est un plan euclidien, le produit scalaire de deux complexes x et y étant la partie réelle du produit de x par le conjugué de y.
- De manière plus générale, tout espace hermitien de dimension n hérite d'une structure d'espace euclidien de dimension 2n, avec comme produit scalaire la partie réelle du produit scalaire d'origine.
Inégalités de Cauchy-Schwarz et de Minkowski
Deux majorations sont largement utilisées dans l'étude des espaces euclidiens.
L'égalité n'a lieu que si x et y sont colinéaires.
Inégalité de Minkowski —
La norme de la somme de deux vecteurs est majorée par la somme de leurs normes :L'égalité n'a lieu que si x et y sont colinéaires et de même sens. Cette majoration correspond au troisième axiome définissant une norme, dit de sous-additivité ou inégalité triangulaire.
Propriétés algébriques
Caractérisation par la forme polaire
Pour toute norme euclidienne ║∙║ sur un ℝ-espace vectoriel E (de dimension finie ou infinie), le carré ║∙║2 est une forme quadratique. Sa donnée suffit à reconstituer le produit scalaire dont dérive la norme ║∙║. On dispose pour cela de trois « formules de polarisation » ou « formes polaires ». Ces trois formules fournissent en outre trois critères pour qu'une norme soit euclidienne :
Identités de polarisation — Une norme ║∙║ sur E est euclidienne si et seulement si l'une des trois applications φ de E×E dans ℝ déduites de ║∙║ par les formules suivantes est bilinéaire. De plus, ces trois applications sont alors égales au produit scalaire dont dérive ║∙║.
On en déduit immédiatement la caractérisation suivante :
Caractérisation par une quadrique — La sphère unité d'un espace vectoriel euclidien est une quadrique compacte non dégénérée centrée en 0. Réciproquement, toute quadrique compacte de E non dégénérée et centrée en 0 est la sphère unité d'un unique produit scalaire sur E.
Il existe un quatrième critère, plus direct, pour déterminer si une norme est euclidienne, sans reconstituer son produit scalaire :
Base orthonormale
Dans un espace vectoriel euclidien, une famille de vecteurs est dite orthonormale si ses vecteurs sont unitaires et deux à deux orthogonaux. C'est alors une base dès qu'elle est génératrice, d'après la propriété suivante :
Orthogonalité et vecteurs libres — Toute famille de vecteurs non nuls et orthogonaux deux à deux est libre.
Si E est un espace euclidien de dimension n et B une base orthonormale de E alors, pour tous vecteurs u et v de E, de coordonnées x et y dans B, le produit scalaire 〈u, v〉 est égal au produit scalaire 〈x, y〉 dans l'espace euclidien canonique de dimension n. Autrement dit, la bijection linéaire de E dans ℝn qui associe à tout vecteur ses coordonnées dans B respecte les deux produits scalaires et constitue ainsi un isomorphisme d'espaces euclidiens.
Projeté orthogonal
Soient F un sous-espace vectoriel de E et x un vecteur de E. La preuve de l'inégalité de Bessel permet — en admettant provisoirement (cf. section suivante) l'existence de bases orthonormales pour tout espace euclidien — de construire[6] le projeté orthogonal de x sur F, c'est-à-dire le vecteur p(x) de F tel que x – p(x) soit orthogonal à F. On prouve ainsi l'existence d'un tel projeté, et son unicité est garantie par le fait que F et son orthogonal n'ont en commun que le vecteur nul. Par le théorème de Pythagore, la norme de p(x) est inférieure ou égale à celle de x :
Projeté orthogonal et inégalité de Bessel — Soit (fi) une base orthonormale de F. Pour tout vecteur x de E, le vecteur
est le projeté orthogonal de x sur F. Ses coordonnées 〈x, fi〉 sont appelées coefficients de Fourier, et la somme de leurs carrés est inférieure ou égale au carré de la norme de x.
Procédé de Gram-Schmidt
Le théorème précédent permet, si x n'appartient pas à F, de construire une base orthonormée de F ⊕ ℝx, en adjoignant à celle de F le vecteur non nul x – p(x) divisé par sa norme. On prouve ainsi l'existence de bases orthonormales pour un espace euclidien, par récurrence sur sa dimension. C'est le principe de l'algorithme de Gram-Schmidt, qui en calcule une explicitement, à partir de la donnée préalable d'une base ordinaire :
Existence d'une base orthonormale — Tout espace euclidien possède une base orthonormale.
Orthogonalité et convexité
Soient E, F et p comme ci-dessus. La projection orthogonale p est un projecteur sur F, c'est-à-dire une application linéaire et idempotente d'image F. Son noyau F⊥ est donc un supplémentaire de F :
Théorème du supplémentaire orthogonal — Dans un espace vectoriel euclidien, tout sous-espace et son orthogonal sont supplémentaires.
On pouvait d'ailleurs le prévoir en remarquant que la codimension de F⊥ est égale à la dimension de F (dans un espace préhilbertien de dimension infinie, ces arguments ne sont plus disponibles et sont remplacés par le théorème du supplémentaire orthogonal d'un sous-espace complet).
D'après le théorème de Pythagore, p(x) est l'élément de F le plus proche de x. On peut aussi construire p(x) via cette propriété de minimisation de la distance (puis en déduire sa première caractérisation), comme cas particulier du théorème suivant. (Ce théorème s'applique à F qui, comme tout sous-espace vectoriel de E, est fermé et convexe.)
Théorème de projection sur un convexe fermé — Soient C un convexe fermé non vide de E et x un vecteur de E. Il existe un unique vecteur PC(x) de C, dit projeté de x sur le convexe, tel que la distance de x à C soit égale à celle de x à PC(x).
Espace dual et forme bilinéaire
L'application φ de E dans son dual E*, qui à tout vecteur x de E associe la forme linéaire x* définie par :
est clairement linéaire, et de noyau nul donc injective. De l'égalité des dimensions de E et de E* il résulte que φ est aussi surjective. On a donc :
est un isomorphisme.
Lorsque E* est muni de la norme duale, cet isomorphisme est même une isométrie (d'après l'inégalité de Cauchy-Schwarz), ce qui prouve que cette norme est euclidienne, c'est-à-dire associée à un produit scalaire : celui importé de E par φ. (L'analogue de ces résultats pour un espace de Hilbert de dimension infinie est le théorème de représentation de Riesz.)
L'isomorphisme φ est très largement utilisé, en mathématiques comme en physique. Par exemple un champ scalaire, c'est-à-dire une application différentiable de E dans ℝ, possède comme différentielle une application de E dans l'ensemble des formes linéaires sur E. L'identification du dual et de E à l'aide de l'isomorphisme φ permet de représenter les formes linéaires sur E par des éléments de E. La différentielle prend alors le nom de gradient. En physique, la force est un élément du dual des vecteurs de l'espace géométrique. Elle est identifiée à un vecteur de l'espace, même si elle n'est pas de même nature. Cette technique permet une représentation plus intuitive ainsi qu'un calcul simple. Le travail de la force, une grandeur importante en physique, s'interprète comme le produit scalaire avec la force.
Pour tout espace vectoriel F, on déduit de φ un isomorphisme canonique a ↦ φ∘a, de L(F, E) dans L(F, E*), lui-même canoniquement isomorphe aux deux espaces de formes bilinéaires L2(F, E) et L2(E, F). Pour F = E, on obtient ainsi deux isomorphismes ψ1 et ψ2, de L(E) dans L2(E, E) :
Adjoint d'un endomorphisme
Sur un espace euclidien E, pour tout endomorphisme a, il existe un unique endomorphisme a* tel que
En effet, cette propriété équivaut à a* = (ψ2−1∘ψ1)(a), où ψ1 et ψ2 sont les deux isomorphismes ci-dessus.
Définitions et propriété — L'adjoint d'un endomorphisme a de E est l'endomorphisme a*. Les endomorphismes égaux (resp. opposés) à leur adjoint sont dits symétriques (resp. antisymétriques). L'automorphisme a ↦ a* de L(E) est involutif.
Cet automorphisme de L(E) est donc la symétrie par rapport au sous-espace des endomorphismes symétriques, par rapport à celui, supplémentaire, des antisymétriques.
La relation induite par le produit scalaire entre les formes bilinéaires et les endomorphismes possède de nombreuses applications, dans des domaines très divers (voir notamment l'article théorème spectral dans le cas où les formes et les endomorphismes sont symétriques).
Tout endomorphisme symétrique ou antisymétrique est normal, c'est-à-dire qu'il commute avec son adjoint.
Une autre famille importante d'endomorphismes normaux est celle des automorphismes orthogonaux, c'est-à-dire inverses de leur adjoint ou encore qui laissent invariant le produit scalaire, autrement dit : qui sont des isométries de E. Ces isométries forment un groupe appelé groupe orthogonal et noté O(E).
Construction d'espaces euclidiens
Comme fréquemment en algèbre, la donnée d'espaces euclidiens permet d'en construire de nouveaux.
Sous-espace, espace produit
Si F est un sous-espace vectoriel d'un espace euclidien, alors la restriction du produit scalaire induit une structure d'espace vectoriel euclidien sur F.
Si E1 et E2 sont deux espaces euclidiens, alors leur produit est naturellement muni d'un produit scalaire, défini par
Espace quotient
Tout espace vectoriel normé quotient E/F d'un espace euclidien E par un sous-espace vectoriel F est isomorphe au supplémentaire orthogonal F⊥, par l'isométrie qui à toute classe dans E/F associe son élément de norme minimum : le projeté orthogonal sur F⊥ commun à tous les éléments de cette classe. La norme sur E/F est donc euclidienne, c'est-à-dire associée à un produit scalaire : celui importé de F⊥ (sous-espace euclidien de E) par cette isométrie.
Produit tensoriel
Soient E1 et E2 deux espaces euclidiens. Le produit tensoriel 〈⋅, ⋅〉1⊗〈⋅, ⋅〉2 de leurs produits scalaires respectifs est une forme bilinéaire sur le produit tensoriel E1⊗E2, qui s'exprime sur les générateurs canoniques de cet espace vectoriel par :
Cette forme bilinéaire hérite donc de la symétrie des deux produits scalaires, et si (ei) est une base orthonormée de E1 et (fj) une base orthonormée de E2 alors la base (ei⊗fj) de E1⊗E2 est orthonormée pour cette forme, ce qui prouve que c'est un produit scalaire.
Si E1 et E2 sont égaux à un même espace euclidien F, la symétrie de E := F⊗F qui les échange est orthogonale pour ce produit scalaire. L'espace L2(F, F) est canoniquement isomorphe à E* donc hérite d'une structure euclidienne, transportée de celle de E par l'isomorphisme φ.
Endomorphisme
Pour tout espace euclidien E, l'espace L(E), canoniquement isomorphe à E*⊗E, hérite de même d'un produit scalaire, pour lequel les isomorphismes ψ1 et ψ2 sont des isométries.
Ce produit scalaire s'exprime de façon simple grâce aux notions d'adjoint et de trace :
Lorsque les endomorphismes sont représentés par des matrices dans une base orthonormée fixée, on retrouve ainsi le produit scalaire canonique sur Mn(ℝ).
Pour ce produit scalaire, la symétrie a ↦ a* est un automorphisme orthogonal de L(E).
Topologie
Caractérisation par le groupe orthogonal
Le groupe orthogonal O(E) d'un espace euclidien E est naturellement muni d'une structure de groupe topologique et même de groupe de Lie : pour tout espace vectoriel réel V de dimension finie, l'espace L(V) de ses endomorphismes est également de dimension finie donc muni d'une topologie canonique. Le groupe linéaire GL(V) des automorphismes de V, ouvert dans L(V), hérite ainsi d'une structure de groupe de Lie. Si E est un espace euclidien, O(E) est un groupe de Lie compact, comme sous-groupe compact de GL(E).
Fonctorialité du groupe orthogonal — Soient E et F deux espaces euclidiens. Tout morphisme d'espaces euclidiens de E dans F induit fonctoriellement un morphisme de groupes topologiques de O(E) dans O(F).
En effet, E s'identifie dans ce cas à un sous-espace de F, et O(E) au sous-groupe de O(F) constitué des automorphismes qui fixent chaque vecteur de l'orthogonal de E dans F.
Ainsi, tous les espaces euclidiens de dimension n ont le « même » groupe orthogonal que celui, noté O(n), de l'espace euclidien usuel ℝn. Ces groupes sont ipso facto isomorphes en tant que groupes de Lie (c'est-à-dire reliés par un isomorphisme de groupes qui est non seulement un homéomorphisme mais un difféomorphisme).
On peut reformuler l'« unicité » du groupe orthogonal pour chaque dimension en disant que pour tout espace vectoriel V de dimension n et tout sous-groupe G de GL(V), s'il existe sur V un produit scalaire dont G soit le groupe orthogonal, alors G est isomorphe (en tant que groupe topologique) à O(n). La réciproque est vraie :
Le groupe détermine le produit scalaire — Soient V un espace vectoriel réel de dimension n et G un sous-groupe de GL(V). Si G est isomorphe (en tant que groupe topologique) à O(n) alors il est le groupe orthogonal d'un produit scalaire sur V, unique à homothétie près.
L'unicité du produit scalaire n'est vraie qu'à homothétie près car si 〈⋅, ⋅〉 est un produit scalaire et si λ est un réel non nul, alors le groupe orthogonal du produit scalaire 〈λ⋅, λ⋅〉 est le même que celui de 〈⋅, ⋅〉.
Son existence est bien plus profonde. L'une des approches possibles pour la démontrer[7] puise son inspiration dans la théorie de la représentation des groupes de Lie. Elle est relativement générique (elle s'applique aux espaces affines euclidiens, aux géométries projectives ou encore symplectiques), mais dépasse le cadre de cet article.
Espaces vectoriels normés de dimension finie
Tout espace vectoriel euclidien est, en tant qu'espace vectoriel normé, un exemple d'espace vectoriel topologique séparé.
Les espaces vectoriels réels de dimension finie n'admettent qu'une telle topologie. Une conséquence est que la norme euclidienne est équivalente à toutes les normes, euclidiennes ou non. La structure topologique d'un espace vectoriel normé de dimension finie E possède de nombreuses propriétés :
- toute application linéaire de E dans un espace vectoriel normé est continue ;
- E est uniformément homéomorphe à ℝn ;
- tout sous-espace vectoriel de E est fermé ;
- E est complet ;
- les compacts de E sont ses fermés bornés (voir théorème de Borel-Lebesgue). Réciproquement, un espace vectoriel normé dans lequel toute boule fermée est compacte est de dimension finie (voir théorème de compacité de Riesz).
Généralisations
Il existe plusieurs généralisations des espaces euclidiens. En choisissant comme corps de base le corps des nombres complexes, on obtient la notion d'espace hermitien. De tels espaces admettent une théorie analogue, au prix d'adaptations naturelles : les résultats présentés dans cet article restent intégralement vérifiés pour ces espaces[8].
En dimension infinie, une définition analogue (existence d'un produit scalaire ou hermitien) amène d'abord à la notion de préhilbertien, dans le cas réel et dans le cas complexe. Le caractère complet n'est pas vérifié en général. Un espace préhilbertien, complet pour la topologie d'espace métrique induite par la norme préhilbertienne, est appelé espace de Hilbert. Les espaces de Hilbert font l'objet d'une riche théorie, et sont des objets de base en analyse fonctionnelle[9].
Une géométrie euclidienne est définie par un espace vectoriel et une forme bilinéaire particulière (définie positive). Travailler avec certaines autres formes bilinéaires permet d'obtenir d'autres géométries, par exemple la géométrie symplectique.
Pour d'autres corps de base que les réels ou les complexes, la notion de forme bilinéaire définie positive n'est en général pas pertinente, car le corps n'est pas ordonné. On remplace généralement cette hypothèse par le fait que la forme est non dégénérée, c'est-à-dire qu'il n'existe pas de vecteur non nul orthogonal à tout l'espace. Une telle structure est utilisée, par exemple pour la géométrie sur les groupes finis. Les groupes orthogonaux sur des espaces vectoriels de dimension finie sur les corps finis fournissent notamment des familles infinies de groupes simples[10].
Notes et références
- Une approche de cette nature se trouve dans : Y. Ladegaillerie, Géométrie pour le CAPES de mathématiques, Ellipses, 2002 (ISBN 2729811486).
- De dimension non nécessairement finie : cf. l'article « Espace préhilbertien ».
- Cette définition se généralise aux espaces vectoriels complexes : cf. l'article « Hermitien ».
- Monier 2007, p. 121.
- Le terme d'espace vectoriel canonique pour ℝn est largement utilisé, on peut citer : R. Godement, « Domaines fondamentaux des groupes arithmétiques », dans Séminaire Bourbaki, tome 8, 1962 à 1964, Exposé no 257.
- Cette technique possède des applications, par exemple, en statistique, et elle est le fondement de la méthode des moindres carrés.
- Pour une autre approche, voir Lemme d'unitarisation.
- Cette généralisation est traitée par exemple dans Serge Lang, Algèbre [détail des éditions].
- Cette généralisation est traitée par exemple dans : Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions], p. 78 à 116.
- Une référence standard mais technique : R. W. Carter, Simple Groups of Lie Type, Wiley & Sons, 1993 (ISBN 0-471-50683-4).
Voir aussi
Bibliographie
- Jean-Marie Monier, Cours de mathématiques : MPSI, PCSI, PTSI et MP, PSI, PC, PT : Algèbre et géométrie MP, t. 8, Paris, Dunod, , 5e éd., 331 p. (ISBN 978-2-10-051038-2, lire en ligne)
- Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques : Géométrie et cinématique, vol. 3 : Géométrie et cinématique, Dunod, , 733 p. (ISBN 978-2-10-005716-0)
- Edmond Ramis, Claude Deschamps et Jacques Odoux, Cours de mathématiques, vol. 5 : Applications de l'analyse à la géométrie, Dunod, , 2e éd. (ISBN 978-2-10-004178-7)
Liens externes
- Espaces euclidiens un cours niveau Maths PCSI par S. Gonnord
- Espaces euclidiens sur le site les-mathematiques.net, par C. Antonini et al., 2001
- Espace euclidien de Ross Moore de l'université Macquarie, traduit par Abderemane Morame de l'université de Nantes, 2006.

























