Isométrie
En géométrie, une isométrie est une transformation, qui conserve les longueurs et les mesures d’angles, délimités par deux demi‑droites ou bien deux demi‑plans. Autrement dit, une isométrie est une similitude particulière, qui reproduit n’importe quelle figure à l’échelle 1. Ce rapport 1 de longueurs s’appelle le rapport de la similitude.
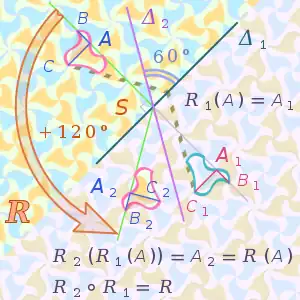
isométries indirectes, cette rotation de + 120°
est une isométrie directe.
Comme une similitude, une isométrie dite directe conserve l’orientation des figures, tandis qu’une isométrie indirecte inverse leur orientation. Par exemple, une translation est une isométrie directe. En géométrie plane une symétrie axiale, ou bien en géométrie dans l'espace une symétrie orthogonale par rapport à un plan est une isométrie indirecte.
Le terme isométrie est parfois un peu vague. Il peut renvoyer à deux termes distincts. Une isométrie peut désigner :
- une isométrie vectorielle, il sera alors plus prudent de parler de transformation unitaire ou, si l'espace de départ et d'arrivée sont égaux, d'automorphisme orthogonal ;
- une isométrie affine, c’est-à-dire une transformation bijective d'un espace affine euclidien dans un autre qui conserve les distances. On généralise cette notion aux transformations bijectives d'un espace métrique dans un autre qui conservent les distances.
Dans le cas particulier de l'espace de Minkowski, associé à la relativité restreinte, les isométries sont les transformations affines qui préservent la pseudo-métrique liée à l'intervalle d'espace-temps et forment le groupe de Poincaré.
Mathématiquement parlant, une application où est un espace vectoriel muni d'une (pseudo-)métrique est une isométrie si elle vérifie :
pour tous vecteurs de .
Les isométries sont les seules transformations à la fois absolument sous-identitaires et absolument sur-identitaires.




