Groupe diédral

Le groupe D_2n peut être défini par la suite exacte scindée suivante :

${\displaystyle 1\to C_{n}\to D_{2n}\to C_{2}\to 1}$

où C_n (également noté Z_n ou Z/nZ) est un groupe cyclique d'ordre n, C₂ est cyclique d'ordre 2, la section étant donnée par l'action d'un relevé σ du générateur de C₂, sur un générateur τ du groupe cyclique d'ordre n :

${\displaystyle \sigma \tau \sigma ^{-1}=\tau ^{-1}.}$

Ce groupe est donc produit semi-direct de C_n par C₂ suivant le morphisme ψ, où l'unité de C₂ agit sur C_n comme l'application identique et l'autre élément de C₂ agit sur C_n par inversion[3]. Explicitement :

${\displaystyle {\text{si }}\;C_{n}=\langle \tau \rangle ,\;C_{2}=\langle \sigma \rangle \;{\text{ alors }}\;\psi (1)(\tau ^{k})=\tau ^{k},\psi (\sigma )(\tau ^{k})=\tau ^{-k}\quad \forall k\in \{0,1,2,...,n-1\}.}$

Une présentation est alors :

${\displaystyle \left\langle \sigma ,\tau \mid \sigma ^{2},\tau ^{n},\sigma \tau \sigma ^{-1}\tau \right\rangle ,}$

c'est-à-dire que des générateurs sont σ, τ et les seules relations qu'ils vérifient sont celles résultant (par les axiomes sur une loi de groupe) de :

${\displaystyle \sigma ^{2}=1,\quad \tau ^{n}=1\quad {\text{et}}\quad \sigma \tau \sigma ^{-1}=\tau ^{-1}.}$

On peut ainsi dresser une liste complète des éléments du groupe :

${\displaystyle 1,\tau ,\tau ^{2},\dots ,\tau ^{n-1},\sigma ,\sigma \tau ,\sigma \tau ^{2},\dots ,\sigma \tau ^{n-1}}$

Une présentation alternative, où μ = τσ dans le système de générateurs de la présentation précédente, est :

${\displaystyle \left\langle \sigma ,\mu \mid \sigma ^{2},\mu ^{2},(\mu \sigma )^{n}\right\rangle ,}$

c'est-à-dire que des générateurs sont σ, μ et les seules relations qu'ils vérifient résultent de :

${\displaystyle \sigma ^{2}=1,\quad \mu ^{2}=1\quad {\text{et}}\quad (\mu \sigma )^{n}=1.}$

On voit ainsi que le groupe diédral admet un système de deux générateurs distincts tous deux d'ordre 2. Les groupes diédraux sont les seuls groupes finis possédant cette propriété[4].

Le groupe diédral d'ordre 2n peut aussi être vu comme le groupe des automorphismes du graphe constitué seulement d'un cycle avec n sommets (si n ≥ 3).

On peut définir de la façon suivante une représentation du groupe diédral D_2n :

${\displaystyle \varphi :D_{2n}\to \mathrm {GL} _{2}(\mathbb {R} )}$

${\displaystyle {\text{avec}}\quad \varphi (\tau )={\begin{pmatrix}\cos(2\pi /n)&-\sin(2\pi /n)\\\sin(2\pi /n)&\cos(2\pi /n)\end{pmatrix}}\quad {\text{et}}\quad \varphi (\sigma )={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.}$

Cette représentation est en fait à valeurs dans le groupe orthogonal O(2,R).

On reconnaît que la matrice φ(τ) est une matrice de rotation d'angle 2π/n et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant un polygone régulier centré en l'origine à n côtés.

Les sous-groupes finis de O(2,R) sont cycliques ou diédraux[5].

Les graphes de cycles de groupes diédraux sont constitués d'un cycle à n éléments et de cycles à 2 éléments. Le sommet sombre dans les graphes de cycle ci-dessous de divers groupes diédraux représente l'élément identité, et les autres sommets sont les autres éléments du groupe. Un cycle est constitué des puissances successives de l'un ou l'autre élément connecté à l'élément identité.

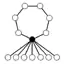D4	D6	D8	D10	D12	D14

Le sous-groupe ⟨τ⟩ = {1, τ, τ², …, τ^n–1} des rotations est normal et même, si n ≥ 3, caractéristique.

Certaines propriétés des groupes diédraux D_2n avec n ≥ 3 dépendent de la parité de n. Elles peuvent souvent facilement être déduites de la représentation géométrique de ce groupe.

• Le centre Z(D_2n) de D_2n est constitué seulement de l'identité si n est impair, mais si n est pair le centre a deux éléments : l'identité et l'élément τ^n/2, si bien que le groupe quotient D_2n/Z(D_2n) est isomorphe à D_2n si n est impair et à D_n si n est pair. Par conséquent, un groupe diédral est nilpotent si et seulement si son ordre est une puissance de deux[6], et la classe de nilpotence du groupe diédral d'ordre 2^r, avec r > 1, est égale à r – 1[7].
• Le sous-groupe dérivé de D_2n est ⟨[σ, τ]⟩ = ⟨τ²⟩ (égal à ⟨τ⟩ si n est impair)[8]. Le groupe D_2n est donc résoluble de classe ≤ 2 (de classe 2 si n ≥ 3 et de classe 1 si n = 1 ou 2). Les groupes diédraux illustrent ainsi le fait que la classe de nilpotence d'un groupe nilpotent ne peut pas être majorée en fonction de sa classe de résolubilité[9] (alors que sa classe de résolubilité peut être majorée en fonction de sa classe de nilpotence).
• Pour n impair, le groupe D_4n est isomorphe au produit direct de D_2n et d'un groupe cyclique d'ordre 2. Cet isomorphisme est donné par :${\displaystyle D_{4n}\to D_{2n}\times C_{2},\quad \sigma ^{h}\tau ^{k+\epsilon n}\mapsto (\sigma ^{h}\tau ^{k},\epsilon )}$h et ${\displaystyle \epsilon }$ étant définis modulo 2, et k modulo n. Les générateurs des groupes diédraux sont choisis comme dans la première partie de l'article.
• Dans D_2n, toutes les réflexions sont conjuguées les unes des autres dans le cas où n est impair, mais elles sont contenues dans deux classes de conjugaison si n est pair.
• Si m divise n, alors D_2n a n/m sous-groupes de type D_2m, et un sous-groupe cyclique C_m. Par conséquent, le nombre total de sous-groupes de D_2n (n ≥ 1), est égal à d (n) + σ (n), où d (n) est le nombre de diviseurs positifs de n et σ (n) est la somme des diviseurs positifs de n (voir liste des petits groupes pour les cas n ≤ 8).

Si n est impair, le groupe D_2n admet 2 représentations irréductibles complexes de degré 1 :

${\displaystyle \sigma \mapsto (-1)^{k}\;\tau \mapsto 1\;k\in \{0,1\}.}$

En revanche, si n est pair, il existe 4 représentations irréductibles de degré 1 :

${\displaystyle \sigma \mapsto (-1)^{k}\;\tau \mapsto (-1)^{h}\;k\in \{0,1\}\;h\in \{0,1\}.}$

Les autres représentations irréductibles sont toutes de degré 2 ; elles sont en nombre ${\displaystyle {\frac {n-1}{2}}}$ si n est impair, respectivement ${\displaystyle {\frac {n}{2}}-1}$ si n est pair. On peut les définir comme suit :

${\displaystyle \tau \mapsto {\begin{pmatrix}\omega ^{h}&0\\0&\omega ^{-h}\end{pmatrix}}\quad {\mbox{ et }}\quad \sigma \mapsto {\begin{pmatrix}0&-1\\-1&0\end{pmatrix}}}$

où ω désigne une racine primitive n-ième de l'unité, et h parcourt les entiers compris entre 1 et n – 1. On peut vérifier que deux telles représentations sont isomorphes seulement pour h₁ et h₂ vérifiant h₁ + h₂ = n. On obtient alors le nombre annoncé de représentations irréductibles de degré 2 non isomorphes, et donc toutes les représentations irréductibles du groupe diédral, par la formule liant le nombre de représentations irréductibles à l'ordre du groupe.

Le groupe des automorphismes de D₂ = Z₂ est trivial. Celui du groupe de Klein D₄ = Z₂ × Z₂ est le groupe non abélien d'ordre 6 : GL(2, F₂) ≃ S₃ ≃ D₆ (en).

Pour n ≥ 3, le groupe Aut(D_2n) des automorphismes de D_2n = Z_n⋊Z₂ est l'holomorphe Hol(Z_n) = Z_n⋊Aut(Z_n) ≃ Z_n⋊Z^×
_n du sous-groupe caractéristique Z_n. En effet, fixons un élément σ de D_2n\Z_n puis, pour tout automorphisme f de D_2n, notons h_f l'élément σ f(σ) et k_f la restriction de f à Z_n. On vérifie alors que l'application f ↦ (h_f, k_f) est un isomorphisme de Aut(D_2n) dans Z_n⋊Aut(Z_n)[10].

Pour n ≠ 2, le groupe Aut(D_2n) est donc d'ordre nφ(n), où φ est l'indicatrice d'Euler.

Le sous-groupe des automorphismes intérieurs est isomorphe à D_2n/Z(D_2n), donc (voir supra) à D_2n si n est impair et à D_n si n est pair.

Les seules valeurs de n pour lesquelles les deux groupes Aut(D_2n) et D_2n ont même ordre, c'est-à-dire pour lesquelles φ(n) = 2, sont n = 3, 4 et 6. Pour ces trois valeurs, Aut(D_2n) ≃ Z_n⋊Z^×
_n ≃ Z_n⋊Z₂ = D_2n[10].

Le groupe diédral infini (en)[11] D_∞ est défini comme le groupe diédral généralisé (voir infra) du groupe monogène infini C_∞ = Z :

${\displaystyle D_{\infty }:=Dih(\mathbb {Z} )=\mathbb {Z} \rtimes C_{2}=\mathrm {Hol} (\mathbb {Z} )=\left\langle \sigma ,\tau \mid \sigma ^{2},\sigma \tau \sigma ^{-1}\tau \right\rangle .}$

En posant μ = τσ, on voit qu'il est isomorphe au produit libre C₂ * C₂ :

${\displaystyle D_{\infty }=\left\langle \sigma ,\mu \mid \sigma ^{2},\mu ^{2}\right\rangle .}$

Son centre est trivial.

On peut interpréter D_∞ comme le groupe d'automorphismes du graphe constitué d'un chemin infini dans les deux sens. De façon équivalente, il s'agit du groupe des isométries de Z.

Aut(D_∞) est égal à D_∞⋊Z₂, où le sous-groupe normal D_∞ est constitué des automorphismes intérieurs et où l'action de Z₂ sur D_∞ = C₂ * C₂ consiste à échanger les deux facteurs. Par conséquent[10] :

${\displaystyle Aut(D_{\infty })=\left\langle \sigma ,\mu ,\nu \mid \sigma ^{2},\mu ^{2},\nu ^{2},\nu \sigma \nu \mu ^{-1}\right\rangle =\left\langle \sigma ,\nu \mid \sigma ^{2},\nu ^{2}\right\rangle \simeq D_{\infty }.}$

Pour tout groupe abélien H, le groupe diédral généralisé (en) de H, noté Dih(H), est le produit semi-direct de H par C₂, l'action de C₂ sur H étant l'inversion, i. e.

${\displaystyle \mathrm {Dih} (H)=H\rtimes _{\varphi }C_{2},}$

où φ(0) est l'application identité et φ(1) l'inversion des éléments.

On obtient ainsi, si H et C₂ sont tous deux notés additivement :

(h₁, 0) * (h₂, t₂) = (h₁ + h₂, t₂)

(h₁, 1) * (h₂, t₂) = (h₁ − h₂, 1 + t₂)

pour tous h₁, h₂ dans H et t₂ dans C₂.

(Si C₂ est noté multiplicativement, ces deux formules se résument en (h₁, t₁) * (h₂, t₂) = (h₁ + t₁h₂, t₁t₂) .)

Le sous-groupe de Dih(H) constitué des éléments de la forme (h, 0) est un sous-groupe normal d'indice 2, isomorphe à H. Quant aux éléments de la forme (h, 1), chacun est son propre inverse.

Les classes de conjugaison sont

• les ensembles {(h,0 ), (−h,0 )} ;
• les ensembles {(h + k + k, 1) | k dans H }.

Ainsi, pour tout sous-groupe M de H, les éléments correspondants (m,0) forment aussi un sous-groupe normal de Dih(H) isomorphe à M, et l'on a :

Exemples :

• D_2n = Dih(C_n).
  • Si n est pair, il y a deux ensembles de la forme {(h + k + k, 1) | k dans H }, et chacun d'eux engendre un sous-groupe normal isomorphe à D_n. Ce sont deux sous-groupes du groupe des isométries d'un n-gone régulier, isomorphes mais distincts : tous deux contiennent les mêmes rotations, mais dans l'un des deux sous-groupes, chaque réflexion fixe deux des sommets, tandis que dans l'autre, les réflexions ne fixent aucun sommet.
  • Si n est impair, il n'y a qu'un ensemble de la forme {(h + k + k, 1) | k dans H }.
• D_∞ = Dih(Z) ; il y a deux ensembles de la forme {(h + k + k, 1) | k dans H }, et chacun d'eux engendre un sous-groupe isomorphe à D_∞. Ce sont deux sous-groupes du groupe des isométries de Z, isomorphes mais distincts : tous deux contiennent les mêmes translations (par les entiers pairs), mais dans l'un des deux sous-groupes, chaque réflexion a un point fixe entier (son centre), tandis que dans l'autre, les réflexions sont sans point fixe entier (leurs centres sont des demi-entiers).
• Dih(S¹) est isomorphe au groupe orthogonal O(2,R) des isométries du plan euclidien qui fixent l'origine ou de façon équivalente, au groupe des isométries du cercle. Les rotations forment le groupe SO(2,R), isomorphe au groupe additif R/Z, et également isomorphe au groupe multiplicatif S¹ égal au cercle unité (constitué des nombres complexes de module 1). Dans ce dernier cas, l'une des réflexions (qui, avec les rotations, engendre tout le groupe), est la conjugaison complexe. Les sous-groupes normaux propres ne contiennent que des rotations. Les sous-groupes normaux discrets sont, pour chaque entier n, un sous-groupe cyclique d'ordre n, et les quotients sont isomorphes au même groupe Dih(S¹).
• Dih(Rⁿ ) est le groupe des translations et symétries centrales de Rⁿ (qui, si n > 1 n'épuisent pas toutes les isométries).
• Dih(H) pour n'importe quel sous-groupe de Rⁿ, par exemple un groupe discret ; dans ce cas, s'il agit dans les n directions, c'est un réseau.
  • Les sous-groupes discrets de Dih(R² ) qui contiennent des translations dans une seule direction sont les groupes de frise de types ∞∞ et 22∞.
  • Ceux qui contiennent des translations dans deux directions sont les groupes de papier peint de types p1 et p2.
  • Les sous-groupes discrets de Dih(R³ ) qui contiennent des translations dans trois directions sont les groupes d'espace de systèmes réticulaires tricliniques.

Dih(H) est abélien si et seulement si le produit semi-direct est direct, c'est-à-dire si et seulement si chaque élément de H est son propre inverse, i. e. H est un 2-groupe abélien élémentaire (en) : Dih(C₂^k) = C₂^k+1.