Algèbre linéaire et espace métrique
Dans cet article les lettres ℂ, ℝ, ℚ et ℤ désignent respectivement le corps des imaginaires encore appelés complexes, des nombres réels, des rationnels et l'anneau des nombres entiers et n un entier strictement positif. L'espace vectoriel ℝn désigne l'ensemble des n-uplets composés de n nombres réels dans un ordre donné. Géométriquement, on les imagine comme les coordonnées d'un point dans un espace muni d'un repère orthonormal. En dimension 2 ou 3, on obtient une représentation du monde physique, à la condition qu'il soit approximé par une géométrie euclidienne.
Définition
Définition[1] — Un réseau Λ de ℝn est un sous-groupe discret de ℝn pour l'addition, tel que le sous-espace vectoriel engendré par Λ soit égal à ℝn.
_hexagone.jpg.webp)
Fig. 2. L'
hexagone est une figure permettant de construire un réseau en dimension 2.
Une telle définition mérite quelques explications. Le choix de ℝn au lieu d'un espace vectoriel réel de dimension n n'est que de peu d'importance. Tout espace vectoriel réel de dimension n est une copie de ℝn et les résultats vrais dans ℝn le sont dans un espace réel de dimension n. On parle d'isomorphisme. Le fait que les points forment un groupe implique la régularité du réseau. Un polygone de sommets des points du réseau, translaté par un déplacement d'un point du réseau à un autre, possède toujours pour sommets des points du réseau. L'exemple de la figure 2 l'illustre. Les points du réseau correspondent à l'intersection du quadrillage, l'hexagone en violet, translaté possède toujours des sommets éléments du réseau. Dans le cadre spécifique d'une partie de ℝn, on peut expliquer le sens du mot discret par l'énoncé suivant :
Proposition — Une partie fermée de ℝn est discrète si et seulement si pour tout réel  , elle ne contient qu'un nombre fini de points à distance inférieure ou égale à
, elle ne contient qu'un nombre fini de points à distance inférieure ou égale à  de l'origine.
de l'origine.
Le groupe ℚn, constitué des points à coordonnées rationnelles, est un exemple de sous-groupe non discret.
La troisième propriété signifie qu'il n'existe pas de sous-espace vectoriel strict contenant le réseau. Si la dimension est égale à 3, alors aucun plan ne contient le réseau. Si un plan entier est couvert et s'il existe un unique point du réseau en dehors d'un plan, la stabilité de l'addition et de la soustraction montre que l'espace entier est couvert. Dire que l'espace est couvert signifie qu'il existe un rayon ρ tel que toute boule de rayon supérieur à ρ contient au moins un point du réseau, et ceci quel que soit son centre.
Tout espace vectoriel E de dimension n sur les nombres complexes est aussi un espace vectoriel réel de dimension 2n. Ainsi, si Λ est un groupe discret qui génère E, en tant qu'espace vectoriel réel, il est un réseau de dimension 2n. De même que ℤn est un réseau de ℝn, Gn est un réseau de ℂn. La lettre G désigne ici les entiers de Gauss, c'est-à-dire les nombres de la forme a + ib où a et b sont des éléments de ℤ.
Base
Existence d'une base — Soit Λ un réseau de ℝn, il existe une famille (bi) de n éléments du réseau, tel que tout élément s'exprime de manière unique comme combinaison linéaire de cette famille, à coefficients dans les nombres entiers. Une telle famille porte le nom de base.
- !(l_{i})\in \mathbb {Z} ^{n}\quad \lambda =\sum _{i=1}^{n}l_{i}b_{i}}
 .
.
_base.jpg.webp)
Fig. 4. Dans un réseau, il existe une famille, illustrée en rouge sur la figure, telle que tout point s'exprime comme
combinaison linéaire de manière unique, des points de la famille.
Il existe plusieurs manières de lire et de démontrer ce théorème. En termes de théorie des groupes, un réseau est un groupe abélien de type fini sans torsion, autrement dit un groupe abélien libre de rang fini.
_existence_d'une_base_dim_2.jpg.webp)
Fig. 3.
Une autre manière de voir les choses est de faire usage de l'algèbre linéaire. On considère le réseau comme un quasi espace vectoriel, à la différence que les scalaires ne sont pas tous inversibles. Les scalaires ici sont égaux aux nombres entiers. Une telle structure porte le nom de module. S'il existe une famille génératrice finie, si le ℤ-module forme un groupe additif sans torsion, le théorème des facteurs invariants est une manière de montrer le résultat.
Ces démonstrations sont bien peu géométriques et n'utilisent guère les outils associés aux réseaux. On peut imaginer une démonstration directe, guidée par l'intuition géométrique qu'apporte une telle structure. Le principe est illustré en dimension 2 sur la figure 3. On considère deux vecteurs libres du réseau, choisis de norme la plus petite possible. La norme est le terme mathématique technique désignant la longueur d'un vecteur. On appelle ces vecteurs α et β. Ils définissent un parallélogramme, en jaune sur la figure 3. La minimalité des normes de α et β permet de montrer que ce parallélogramme ne contient aucun point du réseau autre que ses sommets.
On considère un point λ quelconque du réseau, que l'on peut toujours exprimer comme une combinaison linéaire de α et β si la structure considérée est l'espace vectoriel ℝn. En retranchant à λ le vecteur de coordonnées les parties entières de celles de λ, on obtient un petit vecteur du réseau, à l'intérieur du parallélogramme jaune. Ce principe est un peu analogue à une division euclidienne. Le petit vecteur serait, avec cette analogie, le reste. Le fait qu'il soit dans le parallélogramme et dans le réseau, montre qu'il est nul. Le vecteur λ s'exprime donc comme une combinaison linéaire de α et β avec des coefficients entiers.
Cette démonstration, ainsi que sa généralisation en dimension quelconque est plus simple que les deux citées précédemment. L'usage de la géométrie simplifie l'approche. En revanche, la méthode proposée ici n'est pas effective, à la différence de celle des facteurs invariant, par exemple. Effective signifie que l'on peut, avec cette méthode, construire effectivement une base. Dans le cas général, il est difficile de trouver le vecteur non nul de plus petite norme.
Détails de la démonstration en dimension 2 et généralisation à une dimension quelconque
Le réseau n'est pas limité au vecteur nul, car il engendre l'espace vectoriel ℝn, il existe au moins un vecteur de norme non nul, soit b cette norme. Le disque de centre le vecteur nul et de rayon b intersecte le réseau en un autre point que l'origine et contient un nombre fini du points du réseau. Ce qui montre qu'il existe au moins un vecteur α non nul de plus petite norme dans le réseau. On considère maintenant le réseau diminué des multiples de α. L'ensemble est non vide car sinon le réseau n'engendrerait pas l'espace vectoriel ℝn, le même raisonnement que le précédent montre l'existence d'un vecteur β de longueur minimale, dans le réseau, à l'exception peut-être de quelques multiples de α, correspondant à la bande bleue sur la figure 3. Le gros point bleu est l'origine. Le vecteur α est bien un vecteur non nul de plus petite norme du réseau et vient ensuite β, dont la norme n'est minorée que par celle de α, son inverse et le vecteur nul.
Il n'existe au plus qu'une manière d'écrire un vecteur du réseau comme combinaison linéaire de α et β. En effet, cette propriété est une conséquence du fait que ces deux vecteurs sont libres dans l'espace vectoriel ℝn. Il n'existe qu'une manière d'écrire un vecteur quelconque de ℝn comme combinaison linéaire de α et β, ce qui est en particulier vrai pour les vecteurs du réseau.
Montrons maintenant que tout vecteur du réseau est combinaison linéaire de α et β, à coefficients entiers. Considérons le disque rouge, de centre α et de rayon la norme de β, un tel disque ne peut contenir comme point du réseau, en dehors de sa frontière, que quelques multiples de α dans la zone bleue sur la figure 3, d'après la définition de la norme de β. Le disque vert est de centre β et de rayon la norme de α. Le même raisonnement montre que l'intérieur de ce disque ne peut contenir aucun point du réseau. Le segment [0, α] ne peut contenir que ses extrémités comme point du réseau, il en est de même pour le segment [0, β]. Il en est aussi de même pour [α, β] et [β, α + β] car sinon, en soustrayant α ou β, on aurait une contradiction. En résumé, le parallélogramme, en jaune, de sommets 0, α, β et α + β ne contient aucun autre point du réseau que ses sommets. On remarque que ce parallélogramme est constitué des vecteurs de ℝn ayant deux coefficients compris entre 0 et 1 dans la base (α, β).
Considérons un élément quelconque λ du réseau. Il est nécessairement combinaison linéaire de la base (α, β) de ℝn, et λ = aα + bβ avec a et b réels. L'objectif est de montrer que a et b sont entiers. Soit pa (resp. pb) la partie entière de a (resp. b) et ra (resp. rb) sa partie fractionnaire. Comme α et β sont des éléments du réseau et que pa et pb sont des nombres entiers, paα + pbβ est un point du réseau au même titre que λ. Leur différence, égale à raα + rbβ, est donc dans le réseau. C'est aussi un point du parallélogramme jaune car ses deux coordonnées sont comprises entre 0 et 1. Il existe quatre points du réseau possible, comme une partie fractionnaire est toujours strictement plus petite que 1, la seule valeur possible est 0, ce qui montre que a est égal à pa et b à pb. Autrement dit, les coordonnées de λ dans la base sont entières, ce qui termine la démonstration.
_existence_d'une_base.jpg.webp)
Fig. 5.
Démontrons ce résultat par récurrence sur n. Pour les dimensions 1 et 2, une démonstration est déjà présentée. Supposons la propriété démontrée à l'ordre n − 1 et démontrons la à l'ordre n. Le réseau forme une famille génératrice de ℝn, de toute famille génératrice, il est possible d'extraire une base, il existe donc une sous-famille du réseau de cardinal n qui engendre l'espace entier. Soit (fi), pour i variant de 1 à n, une telle base. Elle n'est pas a priori celle recherchée car rien n'indique que les éléments du réseau s'expriment comme combinaison linéaire à coefficients entiers dans cette base. Soit S l'espace vectoriel engendré par (fi), pour i variant de 1 à n − 1. L'intersection du réseau et de S est un groupe discret engendrant S, il existe une base (bi), pour i variant de 1 à n − 1 de l'intersection du réseau et de S, par hypothèse de récurrence. L'hyperplan S est représenté sur la figure 5, couleur crème, le vecteur nul est le point bleu. La famille (bi) est un bon candidat pour la base recherchée, mais il manque encore un vecteur.
Soit φ une forme linéaire nulle sur S telle que l'image du réseau par φ ne soit pas réduite à 0. Une telle forme existe, sinon le réseau n'engendrerait que l'espace S et pas l'espace entier. L'objectif est de montrer que l'image par φ du réseau est un sous-groupe discret de ℝ, c'est-à-dire qu'il existe un réel strictement positif ε tel que si u est un élément du réseau, l'image du réseau par φ ne contient que la valeur φ(u) entre φ(u) − ε et φ(u) + ε. On remarque que l'on peut supposer u nul ; en effet, si l'image par φ du réseau n'est pas discret, quel que soit ε, il existe deux vecteurs u et v d'images distinctes par φ et dont la différence est, en valeur absolue, inférieure à ε, ce qui montre que l'image par φ de u − v est, en valeur absolue, inférieure à ε.
Pour montrer ce résultat, on va montrer qu'il n'existe qu'un nombre fini de valeurs atteintes par φ sur l'intervalle [−1, 1]. Tous les points du réseau ayant une image par φ dans cet intervalle se trouvent entre les hyperplans affines d'équation φ(x) = − 1 et φ(x) = 1, représentés en bleu sur la figure 5. Soit V le volume de ℝn composé des vecteurs compris entre les deux hyperplans et dont les coordonnées, dans la base (bi), de la projection orthogonale par p sur S, sont toutes comprises entre 0 et 1. Le volume V est représenté en vert sur la figure 5. On remarque que V est bien borné car il représente l'ensemble des vecteurs de ℝn ayant des coordonnées comprises entre 0 et 1 dans la base (bi, ,π). Ici π désigne le vecteur orthogonal à S et d'image égale à 1 par la forme φ. Si δ est un nombre réel, compris entre −1 et 1, et image du réseau par φ, δ possède un antécédent dans V. En effet, il existe un vecteur u du réseau compris entre les deux hyperplans et tel que φ(u) = δ. Le vecteur p(u) est dans S et se décompose sur la base (bi) ; soit (ui) les coordonnées de p(u) dans cette base. Si qi désigne la partie entière de ui et ri la partie fractionnaire :
 .
.
On remarque que q est un élément du réseau car combinaison linéaire de la famille (bi) à coefficients dans ℤ. Son image par φ est nulle car il est élément de S. Le point u − q est constitué de la différence de deux éléments du réseau et fait partie du réseau. L'image de q par φ est nulle et φ est linéaire. Le projeté orthogonal de u − q sur l'hyperplan engendré par S est égal à r, ce qui montre que u − q est bien un élément de V. Le volume V est borné, il ne contient qu'un nombre fini de points du réseau, car le réseau est discret. Il ne peut exister qu'un nombre fini de valeurs prises par l'image du réseau par la fonction φ entre −1 et 1, ce qui montre que la valeur 0 est bien isolée dans cette image.
Soit Δ une droite vectorielle de ℝn non contenue dans S et contenant un point non nul du réseau. L'image par φ de Δ est un groupe discret d'après la démonstration précédente, il existe un point bn de Δ et du réseau de plus petite image a strictement positive par φ ; ce point est représenté en rouge sur la figure 5. Soit enfin un élément λ quelconque du réseau, l'élément λ s'exprime comme une combinaison linéaire de (bi), car cette famille est une base de ℝn. Il faut alors montrer que les différents coefficients sont des entiers :
 .
.
L'image par φ de λ est égale à λna, qui est un élément de a.R, l'image de Δ par φ. On en déduit que λn est entier. Le vecteur λ − λnbn est élément du réseau et de S, ce qui montre que les coordonnées λi sont toutes entières. La famille (bi), pour i variant de 1 à n de ℝn est génératrice du réseau. Le fait qu'elle soit de cardinal n termine la démonstration.
Domaine fondamental
Une zone particulière a été utilisée, dans la démonstration précédente, elle correspond à la zone illustrée en jaune dans la figure 3 pour la dimension 2. Elle correspond à la définition suivante :
Définition[1] — Le domaine fondamental par rapport à une base B, si B est une base (bi) du réseau est l'ensemble des points P :

_domaine_fondamental.jpg.webp)
Fig. 6. Deux domaines fondamentaux ont même volume.
La zone rouge de la figure 6 est un exemple de domaine fondamental. La définition d'un domaine fondamental s'obtient à partir d'une base. Pour les réseaux, comme pour les espaces vectoriels, il existe plusieurs bases et, en conséquence plusieurs domaines fondamentaux. À part en dimension 1, où il n'en existe que deux, ayant la même géométrie, il en existe dans tous les autres cas une infinité. Pour s'en rendre compte il suffit de remplacer le deuxième vecteur de la base par la somme de k fois le premier vecteur et le deuxième. Si k désigne un entier, on a là un moyen de construire une infinité de bases aux géométries différentes. Sur la figure 6, la zone verte est un autre domaine fondamental.
Il existe un invariant associé au réseau. Le covolume d'un réseau est le volume du domaine fondamental. Sur la figure 6, les volumes définis par les parallélépipèdes vert et rouge sont égaux.
Invariance du covolume — Le covolume est indépendant de la base qui définit le domaine fondamental.
En effet[2], le covolume de Λ est par définition la valeur absolue du déterminant, dans la base canonique de ℝn, d'une base de Λ, et la matrice de passage d'une base de Λ à une autre appartient au groupe GLn(ℤ) des matrices à coefficients entiers de déterminant ±1.

Fig. 7.
Il existe une manière intrinsèque de définir le domaine fondamental, elle fait appel à des concepts plus avancés. Le groupe de Lie ℝn/Λ dispose d'une mesure canonique. Pour tout point p de ℝn/Λ, il existe un ouvert de p tel que la projection canonique de ℝn dans ℝn/Λ soit un difféomorphisme. Ces difféomorphismes permettent de définir une mesure. Le groupe de Lie est compact ; sa mesure totale peut être choisie égale au covolume du réseau.
Une manière simple de voir les choses est de se limiter à la dimension 2. Les points de première coordonnée égale à un entier sont identifiés avec les points de première coordonnée égale à 0. Cela revient à enrouler l'espace pour obtenir un cylindre où tous les points de première coordonnée entière sont superposés. On identifie alors les points de deuxième coordonnée égale à un entier aux points de deuxième coordonnée égale à 0. Cela revient à enrouler le cylindre pour obtenir un tore, illustré sur la figure 7.
La représentation est, en termes de mesure, imparfaite. Les cercles horizontaux du tore correspondent aux points de deuxième coordonnée constante. Tous ces cercles ont une circonférence égale à 1. Dans la représentation, selon que le cercle est plus ou moins choisi à l'intérieur du tore, la circonférence varie. À ce détail près, la représentation par une forme s'approchant d'une bouée est un bon support pour l'intuition de la géométrie du domaine fondamental d'un réseau.
Groupe orthogonal

Fig. 8. À tout
pavage régulier de l'espace correspond un réseau. Les figures du pavage respectent le
groupe orthogonal.
Le groupe orthogonal d'un espace euclidien est l'ensemble des applications linéaires qui transforment l'espace en lui-même, tout en conservant la distance et les angles. Ces applications sont appelées isométrie. Le groupe orthogonal contient un sous-groupe, appelé groupe spécial orthogonal, composé des transformations de déterminants positifs, nécessairement égaux à 1. En dimension 2, le groupe spécial orthogonal est composé des rotations. Les autres isométries sont les réflexions correspondant à l'image que donne le plan à travers un miroir, qui passe par le point origine. Munis de la loi de composition des applications, le groupe orthogonal est un groupe, ce qui signifie que l'élément neutre, qui laisse les éléments à l'identique, est une isométrie. Si une application est une isométrie, sa réciproque, encore appelé inverse, est encore une isométrie. Enfin, la composition d'isométries est associative.
Définition — Le groupe orthogonal d'un réseau Λ de ℝn est le groupe des applications linéaires du réseau telles que la norme de l'image d'un point λ du réseau soit celle du point λ.
Le terme de norme désigne la norme de la restriction du produit scalaire euclidien au réseau Λ.
Dans le cas d'un réseau, le groupe orthogonal est un groupe fini. Pour s'en rendre compte, il suffit de considérer l'image d'un vecteur d'une base par une isométrie, c'est un vecteur de même norme et il n'en existe qu'un nombre fini. Pour déterminer le groupe orthogonal d'un réseau, on dispose de trois théories différentes.
L'algèbre linéaire classique offre d'autres outils, un élément du groupe orthogonal d'un réseau peut en effet, être prolongé en une isométrie de ℝn, ce qui ramène l'étude à une situation connue. Enfin, une isométrie respecte les distances et les angles, la géométrie euclidienne offre des théorèmes utilisables.
Une manière de visualiser ce groupe orthogonal est d'étudier un pavage régulier de l'espace. Dire que le pavage est régulier revient à dire, dans l'exemple illustré à la figure 8, que les points au centre de chaque étoile forment un réseau. Si l'on regarde un bloc composé des étoiles qui se trouvent à la même distance qu'une étoile donnée, on trouve un hexagone. À la couleur près, réaliser une rotation de centre, celui d'une étoile et d'angle un sixième de tour, laisse invariant le motif illustré sur la figure et par conséquent le réseau associé. La rotation d'un sixième de tour est élément du groupe orthogonal du réseau. L'analyse géométrique proposée ici ne tient pas compte de la couleur.
Cristallographie
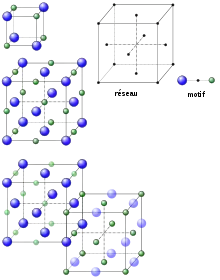
Fig. 9. La
matière solide a tendance à s'organiser en
cristal. Un cristal est un agencement régulier d'
atomes ou d'
ions. Il se caractérise par un réseau et un motif.

Fig. 10. Comprendre la géométrie d'un flocon de
neige impose l'étude d'un
groupe orthogonal d'un réseau de dimension 3
Le groupe orthogonal d'un réseau possède des applications dans les sciences de la nature. À l'état solide, il est fréquent que la matière s'organise autour de la structure d'un réseau. Si ce n'est pas le cas, on parle alors de matière amorphe ou de verre, l'étude devient plus complexe et n'est pas l'objet de cet article.
La matière solide se compose de briques élémentaires, qui peuvent être des atomes, des ions ou des molécules. Ces briques élémentaires disposent de points d'accroches à certains endroits tout à fait précis. Ces briques élémentaires sont en général les mêmes, si la matière est regardée à la bonne échelle. Elles ont tendance à s'assembler de manière régulière, un peu à la manière d'une construction en Lego à partir d'une unique pièce[3]. Cet état est modélisé par un réseau et un motif. Le motif correspond à la géométrie de la brique élémentaire, le réseau indique les points où ces différentes briques se positionnent. Une géométrie de cette nature est illustrée sur la figure 9. Une molécule, composée de deux atomes forme la brique élémentaire, représentée, en haut à droite, par une association d'une bille bleue et d'une verte. Les mêmes molécules s'assemblent selon une géométrie illustrée en haut à gauche. Les points d'accroches forment un angle orthogonal, on obtient un réseau que les cristallographes appellent cubique à faces centrées.
Le groupe orthogonal est source de nombreuses propriétés de cet état de la matière. Il est responsable, par exemple de la forme si caractéristique d'un flocon de neige (figure 10). La régularité du réseau est à l'origine de l'existence de plans de symétries privilégiés, ce qui favorise des tailles particulières pour une pierre précieuse. Cette géométrie détermine aussi son indice de réfraction et partiellement sa couleur[4]. Les propriétés électriques d'un cristal s'expliquent en grande partie à l'aide de cette géométrie[5].
Les cristallographes utilisent un vocabulaire différent de celui des mathématiciens. Il s'explique à la fois par des raisons historiques et par une manière de voir qui n'est pas toujours la même. Un mathématicien parle de structure de groupe pour décrire les propriétés de régularité du réseau. Pour lui, la stabilité de l'addition et de la soustraction est la raison même de cette régularité. Le cristallographe voit une répétition d'un motif à intervalles réguliers. Pour décrire la même propriété, il utilise le terme de périodicité. Le vocable réseau devient réseau de Bravais, groupe orthogonal : groupe ponctuel de symétrie, domaine fondamental maille primitive. Les noms des différents groupes sont aussi modifiés, le terme de groupe de Klein devient : groupe ponctuel orthorhombique et le groupe cyclique d'ordre 2 : groupe ponctuel monoclinique.
Dimension 2
Le cas de la dimension 2, reste encore simple, aucun outil sophistiqué n'est nécessaire pour l'analyser. Uniquement quatre groupes orthogonaux existent :
_sym%C3%A9trie_hexagonale.jpg.webp)
Fig. 11. Il n'existe, à une rotation et une homothétie près, qu'un réseau à symétrie hexagonale.
_sym%C3%A9trie_tetragonale.jpg.webp)
Fig. 12. Si le réseau possède un domaine fondamental carré, le groupe orthogonal est une copie du
groupe diédral D
8.
Classification des réseaux de dimension 2 — Le groupe orthogonal d'un réseau de dimension 2 est isomorphe à l'un des quatre groupes suivants : un groupe diédral D12, D8, D4 ou D2 = C2.
Le plus gros est appelé groupe diédral d'ordre 12 et est noté D12, que les cristallographes le dénomment groupe ponctuel hexagonal. Il est composé de 6 rotations d'un angle de la forme kπ/3 où k désigne un entier, et de 6 réflexions d'axe passant par l'origine et, soit un vecteur non nul du réseau de norme minimale, soit le milieu de deux vecteurs de cette nature. Il n'existe qu'une géométrie pour un réseau correspondant à ce groupe orthogonal. Cela signifie que si deux réseaux ont ce groupe orthogonal, il est possible de passer de l'un à l'autre à l'aide d'une rotation et d'une homothétie. Un réseau de cette nature est illustré sur la figure 11. Il correspond à l'ensemble des combinaisons linéaires à coefficients entiers de deux vecteurs, notés α et β sur l'illustration, de même norme et formant un angle de π/3.
Une configuration analogue présente un groupe orthogonal diédral d'ordre 8, noté D8, que les cristallographes appellent groupe ponctuel tétragonal ou groupe ponctuel quadratique. Le groupe orthogonal contient 4 rotations d'un angle de la forme kπ/4 où k désigne un entier, et de 4 réflexions d'axe passant par l'origine et, soit un vecteur non nul du réseau de norme minimale, soit le milieu de deux vecteurs de cette nature. Un réseau de cette nature est illustré sur la figure 12. Comme précédemment, il est engendré par les combinaisons linéaires à coefficients entiers de deux vecteurs, notés α et β sur l'illustration, de même norme et formant un angle de π/2.
_sym%C3%A9trie_orthorombique.jpg.webp)
Fig. 14. Réseau orthorhombique centré.
_sym%C3%A9trie_orthorombique_(2).jpg.webp)
Fig. 13. Réseau orthorhombique primitif.
Ces deux groupes orthogonaux sont les seuls à ne pas être commutatifs. Le plus vaste des groupes commutatif contient quatre éléments. Si ce groupe peut être vu comme un groupe diédral d'ordre 4, on l'appelle plus souvent le groupe de Klein. Il correspond au groupe à 4 éléments dont chacun est son propre inverse et la somme de deux éléments non nuls est toujours égale au troisième, la table est ainsi facile à bâtir.
Cette fois-ci, il n'existe pas une, mais deux configurations de réseau possibles, illustrés sur les figures 13 et 14. Celle de la figure 13 est obtenue par deux vecteurs, toujours notés α et β, qui sont nécessairement de normes différentes et qui forment un angle de π/2. L'autre solution, illustrée à la figure 14 correspond à deux vecteurs non alignés, de même norme, mais formant un angle nécessairement différent de π/2. Les cristallographes remarquent que l'on passe de la configuration de gauche à celle de droite en ajoutant un point au centre du rectangle de côtés α et β. Ils appellent ces réseaux orthorhombique primitif et orthorhombique centré. Le groupe orthogonal est formé des deux réflexions de centre l'origine et d'axe parallèle à l'un des côtés du rectangle, les deux derniers éléments sont l'identité, qui fait partie du réseau, et la rotation de π.
Le dernier groupe est celui obtenu si aucune des configurations précédentes n'est présente. Le groupe contient deux symétries, l'identité et la rotation de π. La rotation de π transforme un point en son opposé, il laisse stable le réseau et fait toujours partie du groupe orthogonal. Ce groupe est appelé cyclique d'ordre 2 par les mathématiciens et monoclinique par les cristallographes.
Recherche des groupes orthogonaux d'un réseau de dimension 2
Aucun outil sophistiqué n'est nécessaire pour élucider les différentes configurations. On peut s'en tenir aux techniques élémentaires de l'algèbre linéaire et de la géométrie. C'est ainsi que procéda Auguste Bravais[6] pour établir les différentes structures en dimension 2 et 3, au milieu du XIXe siècle, bien avant l'apparition de la définition formelle d'une structure de groupe.
- Groupe diédral d'ordre 12 :
- Le groupe orthogonal contient un sous-groupe commutatif composé des rotations :
- Pour s'en rendre compte, il suffit de remarquer que la composition de deux rotations est encore une rotation et qu'en dimension 2, les rotations commutent. Le groupe orthogonal contient toujours deux rotations, l'identité d'angle 0 et l'application qui à un vecteur associe son opposé, correspondant à la rotation d'un demi tour. Ce qui montre que l'ensemble des rotations n'est jamais vide. Enfin, si une rotation laisse le réseau stable, la rotation inverse laisse aussi nécessairement le réseau stable.
Dans un premier temps, on ne cherche qu'à établir ce sous-groupe encore appelé groupe spécial orthogonal. Il n'existe en fait pas beaucoup de rotations candidates à être dans un tel sous-groupe :
- Si une rotation Θ est dans un groupe orthogonal d'un réseau de dimension 2, son angle est de la forme k.π/3 ou k.π/2, ici k désigne un nombre entier :
- Pour le démontrer, commençons par remarquer que si Θ est une rotation dans le réseau, alors elle transforme une base du réseau en une base composée de vecteurs de même longueur et formant le même angle orienté. Ceci suffit à montrer que Θ peut aussi être vue comme une rotation du plan ℝn.
- On écrit la matrice de la rotation Θ dans une base orthonormale directe, c'est-à-dire composée de deux vecteurs de norme 1 et faisant, un angle orienté de π/4. Dans une telle base, la matrice M de Θ prend la forme suivante, si θ désigne l'angle de la rotation :

- On utilise une astuce, la trace d'une application linéaire, c'est-à-dire la somme des deux coefficients diagonaux dans notre cas, n'est pas modifiée si la base dans laquelle est exprimée l'application linéaire est modifiée. Si l'on choisit une base dans le réseau, la matrice est à coefficients entiers, la trace est donc un nombre entier, ce qui montre que 2cos(θ) est un nombre entier, ou encore que cos(θ) est égal à −1, −1/2, 0, 1/2 ou 1. On trouve bien les valeurs annoncées pour l'angle de la rotation.
Intuitivement, on peut s'en rendre compte en remarquant qu'il est possible de paver l'espace avec des triangles équilatéraux, des carrés ou des hexagones, ce que l'on voit graphiquement dans l'exemple de réseau illustré dans le paragraphe Définition. Un petit dessin montre que c'est impossible avec des pentagones et, pour les polygones réguliers, dès que l'on atteint ou dépasse 7 sommets, on est alors trop proche du cercle pour pouvoir espérer paver l'espace.
- S'il existe une rotation dans le groupe orthogonal d'angle π/3, 2π/3, 4π/3 ou 5π/3 alors le groupe orthogonal contient exactement les six rotations d'angle kπ/3, avec k variant de 0 à 5 :
- Montrons dans un premier temps que la rotation, notée ici Θ, d'angle π/3 est dans le groupe. Soit λ un élément quelconque du réseau, il faut montrer que son image par Θ est bien dans le réseau. La figure de l'hexagone correspondant à ce cas va nous aider. Si la rotation présente dans le groupe, est d'angle π/3, il n'y a rien à démontrer. Si c'est celle d'angle 2π/3, il suffit d'appliquer deux fois à λ la rotation Θ. L'opposé de ce résultat est égal à Θ(λ), ce qui montre que cette valeur est bien dans le réseau et donc que Θ est dans le groupe orthogonal. Si la rotation laissant stable le réseau est celle d'angle 4π/3, il suffit de l'appliquer quatre fois à λ et de remarquer que son opposé est égal à Θ(λ). Enfin, si c'est la rotation d'angle 5π/3, il suffit de l'appliquer cinq fois à λ pour obtenir le résultat voulu.
- Puisque la rotation Θ laisse stable le réseau, l'application deux fois de cette rotation, c'est-à-dire la rotation d'angle 2π/3 est aussi dans le groupe orthogonal. En appliquant cinq fois ce raisonnement, on trouve bien que les six rotations de l'énoncé laissent stable le réseau.
- Il reste à démontrer qu'il n'en existe pas d'autre. D'après un résultat précédent, cela ne pourrait être qu'une rotation d'un quart de tour. Or une rotation d'un quart de tour puis une rotation d'un sixième de tour est une rotation, soit d'un douzième de tour, soit de cinq douzièmes de tour. Aucune de ces deux rotations ne peut faire partie du groupe orthogonal, une rotation d'un quart de tour, dans ce contexte ne peut donc faire partie du groupe orthogonal. La proposition est bien démontrée.
Nous connaissons maintenant toutes les rotations du groupe orthogonal. Pour aller plus loin, on a besoin du vecteur α des illustrations, c'est-à-dire un vecteur du réseau, non nul et de plus petite norme. On utilise aussi β, son image par la rotation d'un sixième de tour. Il est temps de montrer que la configuration du réseau est bien celle de la première figure du paragraphe.
- Tout point du réseau est combinaison linéaire de α et β à coefficients entiers :
- On connaît déjà la configuration du réseau sur le disque de rayon la norme de α et de centre le vecteur nul. Elle correspond exactement à celle de la figure. À l'intérieur du disque, on ne trouve que le vecteur nul car il n'existe pas d'autre vecteur du réseau de norme strictement plus petite que celle de α. Sur la frontière du disque, on trouve les six images de α par les six rotations, à l'image de l'illustration.
- Pour élucider la situation hors du disque, on fait appel à la même astuce que celle utilisée pour démontrer l'existence d'une base en dimension 2. On remarque que le couple (α, β − α) est une base de ℝn, un vecteur λ s'exprime dans cette base. Il ne reste plus qu'à montrer que les deux coordonnées a et b de λ dans cette base sont des entiers. On décompose a = qa + ra et b = qb + rb. Le vecteur qaα + qb(β − α) est combinaison linéaire à coefficients entiers de deux points du réseau, c'est un point du réseau. La différence entre λ et ce vecteur est aussi un point du réseau, égal à raα + rb(β − α). Comme ses coordonnées sont strictement plus petites que 1, cette différence se trouve à être dans le parallélogramme de sommets 0, α, β − α et β. On remarque que ce parallélogramme se trouve à l'intérieur du disque de rayon la norme de α et de centre le vecteur nul. Comme ra et rb sont strictement inférieurs à 1, le seul point du réseau dans cette zone est le vecteur nul. Ceci montre que ra et rb sont nuls et que λ est bien combinaison linéaire de α et β − α à coefficient entiers. Cette propriété est équivalente à celle de la proposition à démontrer.
La détermination est presque terminée. Les rotations ainsi que les points du réseau sont connus, il ne reste plus qu'à déterminer les éléments du groupe orthogonal qui ne sont pas des rotations. Dans un plan, une isométrie vectorielle qui n'est pas une rotation est une réflexion, cette première remarque va nous aider. Une deuxième est utile : la composée de deux réflexions est une rotation et la composée d'une rotation et d'une réflexion est une réflexion. La dernière remarque est que la composée d'une réflexion avec elle-même est l'application identique, on parle d'application involutive :
- Le groupe orthogonal contient exactement 12 éléments et est une copie du groupe diédral D12 :
- Commençons par construire une réflexion, L'application linéaire Γ, qui laisse α stable et qui transforme β en α − β est une réflexion, car elle conserve les distances et les angles d'une base et elle possède une droite invariante et n'est pas l'identité. Si l'on considère les six applications composées de Γ avec Θk pour k variant de 0 à 5, on obtient six réflexions. Le symbole Θk désigne l'application Θ appliquée k fois ou encore la rotation d'angle kπ/3. Les réflexions sont toutes différentes ; pour s'en rendre compte, il suffit d'appliquer ces réflexions puis la réflexion Γ : on obtient six applications différentes, ce qui serait impossible si deux des applications de type Γ.Θk étaient égales. Il ne reste plus qu'à montrer qu'une réflexion Γ est toujours l'une des 6 trouvées. On applique d'abord Γ1 puis deux fois Γ ; on trouve Γ1 car appliquer deux fois Γ revient à ne rien faire. On remarque que Γ.Γ1 est une rotation ; il existe donc une valeur k tel que Γ.Γ1 est égale à Θk. On ré-applique Γ pour obtenir à nouveau Γ1 et l'on trouve que Γ1 est égale à Γ.Θk, l'une des 6 déjà comptabilisées.
- On remarque que Γ et Θ ne commutent pas ; Γ.Θ est la réflexion d'axe dirigé par 2α − β alors que Θ.Γ est la réflexion d'axe dirigé par α + β. Le groupe orthogonal contient 12 éléments dont un d'ordre 6 et est non commutatif. Seules les copies du groupe diédral D12 vérifient toutes ces propriétés.
- Groupe diédral d'ordre 8 :
Il suffit d'appliquer exactement le même raisonnement que pour D4. On trouve que s'il existe une rotation d'un quart de tour, le groupe orthogonal est composé de quatre rotations et de quatre réflexions et que le réseau est engendré par deux vecteurs de plus petites normes α et β, qu'ils ont la même norme et qu'ils forment un angle d'un quart de tour.
On suppose dans toute la suite des démonstrations que la configuration n'est pas l'une de celles déjà traités. Les seules rotations du groupe orthogonal sont l'identité, qui ne bouge aucun vecteur et le demi tour, qui à un vecteur associe son opposé. Il devient utile d'étudier les réflexions un peu plus précisément :
- Il ne peut exister plus de deux réflexions différentes :
- Supposons qu'il existe deux réflexions distinctes Γ1 et Γ2. La rotation Γ1.Γ2 est égale soit à l'identité, soit à son opposée, car ce sont les seules rotations du groupe orthogonal. Si Γ1.Γ2 est égale à l'identité, en appliquant à nouveau Γ1, on trouverait que Γ1 et Γ2 sont égaux, ce qui est contraire à l'hypothèse. On en déduit que Γ1.Γ2 est égale à l'opposé de l'identité et, en appliquant ensuite Γ1, on trouve que Γ2 est égale à −Γ1. Il ne peut en exister une troisième, elle serait aussi égale à −Γ1, donc à Γ2.
- Il n'existe qu'une structure possible pour un groupe orthogonal de plus de deux éléments, le groupe de Klein :
- Le groupe ne contient que deux rotations. Les autres éléments sont des réflexions et il ne peut y en avoir que deux, une notée Γ et son opposé −Γ. Le groupe orthogonal est alors constitué de quatre éléments, chacun étant involutif, c'est-à-dire que l'élément, composé avec lui-même, est égal à l'identité. Il n'existe qu'une structure de groupe composée de 4 éléments étant chacun son propre inverse : le groupe de Klein.
Encore une fois, α désigne un vecteur du réseau non nul et de plus petite norme.
- La structure du groupe orthogonal est celle de Klein s'il existe un vecteur β tel que α et β forment une base du réseau et que, soit β est de même norme que α, soit β est orthogonal à α, mais pas les deux :
- On sait déjà que β ne peut être les deux, le groupe orthogonal serait alors diédral d'ordre 8. On suppose que le groupe orthogonal est de Klein. Il existe quatre isométries involutives. Comme il n'existe que deux rotations involutives, l'identité et son opposé, il existe aussi une réflexion dans le groupe orthogonal. L'image de α par cette réflexion est de même norme que α.
- Si cette image est −α ou α, on note Γ la réflexion qui envoie α sur −α. Elle correspond soit à la réflexion considérée, soit à son opposée. On note β le vecteur du réseau de plus petite norme parmi ceux non colinéaires à α. Le point γ désigne un vecteur colinéaire à l'axe de la réflexion Γ. On va montrer que β est dans l'axe de réflexion de Γ ce qui revient à dire qu'il est perpendiculaire à α. Le couple (α, γ) est une base de ℝn ; on peut exprimer le vecteur β dans cette base : β = aα + cγ ; la coordonnée a est, en valeur absolue, strictement plus petite que 1/2. En effet, si elle était plus grande, le vecteur β − α serait de norme plus petite que celle de β et si a était plus petit que −1/2, le vecteur β + α serait de norme plus petite que celle de β. Le vecteur Γ(β) est un élément du réseau, égal à −aα + cγ, ce qui montre que β − Γ(β), égal à 2aα, est un point du réseau et que 2a est un nombre entier. Comme a est strictement plus petit que 1/2 en valeur absolue et que 2a est un nombre entier, a est nul et β est proportionnel à γ ; c'est un élément de l'axe de la réflexion. Le couple (α, β) est formé d'un vecteur non nul du réseau de plus petite norme et d'un vecteur du réseau non élément de l'axe dirigé par α et de plus petite norme. D'après la démonstration de l'existence d'une base en dimension 2, ces deux vecteurs forment une base du réseau. On a bien trouvé deux vecteurs satisfaisant les hypothèses de la proposition.
- Si l'image β de α par une réflexion n'est ni α, ni −α, le vecteur β est de même norme que α et donc de plus petite norme dans le réseau, à l'exception du vecteur nul. Le point β ne peut être égal à α ou à −α par hypothèse, même si ces points sont de même norme. Ils ne peuvent donc pas être proportionnels. On a montré l'existence de deux vecteurs de norme minimale, à l'exception du vecteur nul, dans le réseau et non colinéaire. Ils forment une base satisfaisant aux hypothèses de l'énoncé.
Il reste encore à démontrer la réciproque :
- La structure du groupe orthogonal est celle de Klein seulement s'il existe un vecteur β tel que α et β forment une base du réseau et que, soit β est de même norme que α, soit β est orthogonal à α, mais pas les deux :
- On suppose que la base (α, β) existe. Le groupe orthogonal contient uniquement deux rotations. Il suffit de montrer qu'il existe une réflexion pour établir la proposition. Si α et β sont de même norme, l'application linaire Γ, qui à α associe β et à β associe α, respecte sur la base (α, β), à la fois la distance et l'angle, c'est une isométrie. Le vecteur α + β est invariant par Γ et Γ n'est pas l'application identité, car l'image de α n'est pas α. L'application Γ est donc une réflexion. Les images de α et β par cette réflexion sont éléments du réseau, donc toute combinaison linéaire à coefficients entiers de ces deux vecteurs est encore élément du réseau. Ceci revient à dire que Γ est une isométrie qui laisse stable le réseau, c'est la définition d'un élément du groupe orthogonal. Le groupe orthogonal contient une réflexion, on a vu que cela signifie que ce groupe est de Klein.
- Si maintenant β est orthogonal à α, l'application linéaire Γ, qui à α associe −α et à β associe β est une réflexion. Le même raisonnement que le précédent permet de conclure.
Il n'existe plus qu'un cas à traiter :
- Groupe cyclique d'ordre 2 :
Si aucune des configurations déjà étudiées n'est présente, le groupe orthogonal contient exactement deux rotations, l'identité et son opposé et aucune réflexion. C'est un groupe à deux éléments, qui est nécessairement le groupe cyclique d'ordre 2, car il n'existe pas d'autre groupe à deux éléments.
Dimension 3
La dimension 3 est de nature analogue à la dimension 2. On trouve cette fois-ci 7 groupes et 14 réseaux de types différents[7].
Classification des réseaux de dimension 3 — Le groupe orthogonal d'un réseau de dimension 3 est isomorphe à l'un des sept groupes suivants : le groupe du cube, isomorphe à S4 × C2, le groupe ponctuel hexagonal D12 × C2, trigonal D12, tétragonal D8 × C2, orthorhombique K × C2, monoclinique K et triclinique C2.
Ici, D2n désigne le groupe diédral d'ordre 2n, Sn désigne le groupe symétrique d'indice n et d'ordre n!, K le groupe de Klein (d'ordre 4) et C2 le groupe cyclique d'ordre 2. On trouve quatre groupes non abéliens d'ordres 48, 24, 16 et 12 puis trois groupes abéliens, d'ordres 8, 4 et 2 et qui ne contiennent que des éléments involutifs.
Trois géométries différentes de réseau présentent une symétrie cubique, illustrées dans la figure 15 ci-dessous. La première, correspondant à l'image de droite, est isomorphe au réseau ℤ3, c'est-à-dire qu'il existe une rotation et une homothétie qui envoie le réseau sur ℤ3. On parle, en cristallographie de réseau cubique primitif. Il existe un domaine fondamental cubique, globalement invariant par toute isométrie du groupe orthogonal. Le deuxième cas est illustré au centre de la figure 15. Il possède comme figure caractéristique, en vert, un cube dont les centres des faces sont occupés par un point. On parle de réseau cubique à faces centrées. Le domaine fondamental illustré n'est plus cubique. Le troisième cas est illustré dans l'image de gauche de la figure 15. Une figure répétitive apparaissant dans le réseau est celui d'un cube dont le centre est aussi élément du réseau, les cristallographes parlent de réseau cubique centré.
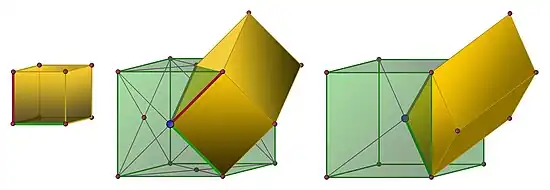
Fig. 15. Il existe trois géométries cubiques pour un réseau. Le cube invariant est illustré en vert, un domaine fondamental en orange.

Fig. 16. Il n'existe qu'une géométrie pour obtenir une structure de réseau hexagonale.
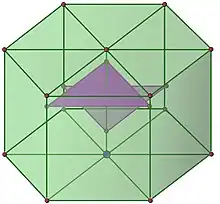
Fig. 17. Ajouter 3 points dessinant un triangle équilatéral bien choisi, forme un réseau de structure trigonale.
Deux géométries contiennent des rotations d'un tiers de tour. La figure 16 correspond à la réplication du réseau hexagonal bidimensionnelle. L'axe orthogonal à un plan contenant le réseau hexagonal de dimension 2, est un axe de symétrie contenant le troisième vecteur δ d'un domaine fondamental. Les isométries trouvées dans le cas de la dimension 2 prolongés sur δ par l'identité sont toutes dans le groupe orthogonal. La symétrie laissant le plan de l'hexagone invariant et transformant δ en −δ est aussi une isométrie laissant invariant le réseau. Le groupe orthogonal est isomorphe à D12 × C2, le produit direct des isométries D12 du réseau hexagonal de dimension deux par le groupe C2 engendré par la symétrie orthogonale transformant δ en −δ.
La figure 17 illustre un réseau contenant un groupe orthogonal plus petit. Le réseau est obtenu par l'adjonction de 6 points supplémentaires à partir de la figure 16. Si δ désigne le plus petit vecteur du réseau orthogonal au plan de l'hexagone, 3 points se trouvent à une hauteur de δ/3 et les trois autres à 2δ/3. Les 3 points à une hauteur de δ/3 forment un triangle équilatéral de même géométrie que ceux qui constituent l'hexagone. Le centre de gravité de ce triangle est à la verticale du centre d'un hexagone et la projection parallèlement à δ, de chaque point du triangle correspond au centre de gravité d'un des triangles de l'hexagone. Les trois derniers points forment un autre triangle, obtenu par rotation d'axe dirigé par δ et d'un demi tour.
Il existe une unique manière de prolonger à tout le réseau une isométrie du groupe orthogonal du réseau hexagonal de dimension 2. Pour la moitié des éléments du groupe, sur δ ce prolongement est l'identité. Pour l'autre moitié, ce prolongement est l'homothétie de rapport −1. Le groupe orthogonal est isomorphe à D12. Avec les rotations du cube, ces deux géométries sont les seules à contenir une rotation d'un tiers de tour. Aucun de ces deux groupes n'est commutatif.

Fig. 18. Il existe deux structures de réseaux tétragonaux : le réseau primitif et celui centré.
Les réseaux tétragonaux ont bien des analogies avec le cas précédent. Il correspond au passage à la dimension 3 du groupe du carré. Pour que les symétries du carré puissent se prolonger en dimension 3, il est nécessaire de placer le dernier point définissant le réseau, sur un axe perpendiculaire au carré et passant, soit par l'un des points du carré soit par son milieu.
Chaque symétrie du carré peut être prolongé par une rotation en dimension 3. Il est possible ensuite de composer l'isométrie par l'homothétie de rapport −1. Ainsi, à chaque isométrie du carré correspond deux prolongements dans la dimension 3. Comme l'homothétie de rapport −1 commute avec toutes les isométries, le nouveau groupe orthogonal est le produit direct de celui de dimension 2 avec C2 qui peut se voir comme l'identité et l'homothétie de rapport −1 dans ℝ3. Ce groupe est le dernier non commutatif.
Une part de convention entre dans la définition des types de réseaux de Bravais. Ainsi, on identifie, pour les groupes ponctuels tétragonaux, les réseaux centrés et ceux à faces centrées. Si l'on considère un réseau centré et que l'on choisit comme figure du carré horizontal, celui formé par deux diagonales, on obtient une figure à face centrée. Cette remarque est aussi vraie pour les réseaux cubiques.

Fig. 19. Les structures orthorhombiques sont au nombre de quatre.
Les autres groupes orthogonaux sont tous commutatifs. Ils se caractérisent pas le fait de ne comporter que des isométries involutives, c'est-à-dire que si on les applique deux fois, on retrouve l'identité. Le plus vaste des groupes de cette nature contient 8 éléments. Il correspond au groupe parfois noté K4 ou encore au produit du groupe de Klein et du groupe cyclique d'ordre 2.
Il existe 4 types de réseaux différents, même s'ils se ressemblent tous. Ils sont construits à partir de 4 vecteurs orthogonaux dont aucun n'a la même taille. Le réseau primitif est un parallélépipède de cette nature. Il existe ensuite trois manières de centrer des points supplémentaires, soit au milieu du parallélépipède, soit au centre de chaque face, soit au centre de deux faces opposées (fig. 19).
S'il existe un axe orthogonal à un plan du réseau, mais que le plan ne contient pas d'axes de symétries, le groupe ne possède plus 8 mais 4 éléments. On trouve alors une structure analogue à celle de la dimension 2 et le groupe ponctuel est de Klein. Elle est composée de deux réflexions opposées, de l'identité et de l'homothétie de rapport −1. Deux types de réseaux distincts, illustrés à la figure 18 possèdent ce groupe orthogonal.
Enfin, si aucune des configurations précédentes n'apparaît, alors il ne reste que deux isométries dans le groupe, l'identité et l'homothétie de rapport −1.
Représentations d'un groupe fini
Si la situation, en dimension 3 est de même nature que celle de la dimension 2, les démonstrations se compliquent un peu. Plusieurs facteurs différenciant la dimension 2 et 3 ne simplifient pas la tâche. Le plus important est probablement le fait que le groupe spécial orthogonal n'a plus de raison d'être abélien, deux rotations ne commutent pas toujours. Ensuite, les groupes sont plus vastes, le plus gros contient 48 éléments en dimension 3, contre 12 en dimension 2. Il est toujours possible d'utiliser les rudiments de l'algèbre linéaire et de la géométrie. La méthode devient plus longue et surtout plus périlleuse. La première classification[8] de Frankenheim (en), datant de 1842, était imprécise. Il a fallu six ans pour que les erreurs soient corrigées par Bravais.
Il est possible d'enrichir l'attirail d'outils plus puissants. Une théorie, à cheval sur celle des groupes et de l'algèbre linéaire est particulièrement adaptée. Elle a pour objet l'étude des morphismes d'un groupe G dans le groupe linéaire d'un espace vectoriel E de dimension finie, qui est choisi complexe et équipé d'un produit hermitien tel que l'ensemble d'arrivée ne contienne que des isométries. On utilise ici quatre résultats. Toute représentation se décompose en une somme directe de représentations irréductibles, résultat connu sous le nom de théorème de Maschke. C'est-à-dire qu'il est possible de décomposer E en une somme directe de sous-espaces orthogonaux entre eux et stables par toutes isométries de la représentation. La restriction de la représentation à un sous-espace stable ne contient aucun sous-espace stable pour chaque isométrie de la représentation, à l'exception des sous-espaces triviaux. Une représentation de cette nature est dite irréductible. Le caractère χφ d'une représentation φ est l'application de G dans ℂ, qui à un élément h de G associe la trace de φ(h). Si g désigne l'ordre du groupe G et φ, ψ deux représentations, on associe aux caractères le produit hermitien suivant :
 .
.
Une représentation est irréductible si, et seulement si, la norme de son caractère est égale à 1. Si deux représentations irréductibles ne sont pas isomorphes, alors le produit hermitien de leurs deux caractères est égal à 0, autrement dit les deux caractères sont orthogonaux. Il existe exactement autant de représentations irréductibles que le nombre de classes de conjugaison du groupe. Enfin, il existe une représentation particulière dite représentation régulière. Pour la construire, on considère que la famille (hi) des éléments du groupe est une base orthonormale d'un espace vectoriel. À h un élément du groupe, on associe l'isométrie qui transforme la base (hi) en la base (h.hi). Une représentation régulière contient autant de copies d'une représentation irréductible que le degré de cette représentation irréductible.
Ordre d'un groupe spécial orthogonal
Dans cette boite déroulante, le terme de groupe orthogonal désigne les isométries d'un réseau de dimension 3, le terme de groupe spécial orthogonal désigne le sous-groupe des isométries de déterminant égal à 1. Commençons par une proposition d'ordre général :
- Toute isométrie du groupe orthogonal est d'ordre 1, 2, 3, 4 ou 6 :
- Soit φ un élément du groupe orthogonal. Sa matrice M, à la puissance l'ordre du groupe est égale à l'identité, d'après le théorème de Lagrange. Ceci montre que M est diagonalisable. L'endomorphisme φ admet aussi une matrice à coefficients entiers ; on en déduit qu'il existe un nombre complexe ω tel que la matrice M est semblable à Mω, avec :

- La trace de Mω est un nombre entier ; on en déduit que la somme de ω et de son conjugué est un nombre entier, ce qui montre le résultat.
Le théorème de Cauchy, conséquence directe d'un théorème de Sylow, montre que si n est un nombre premier facteur de l'ordre du groupe, alors il existe un élément du groupe d'ordre n. On en déduit que l'ordre du groupe orthogonal est de la forme 2p.3q, où p et q sont des entiers positifs. Dans un premier temps, on cherche à déterminer la structure d'un groupe spécial orthogonal, c'est-à-dire des isométries du réseau de déterminant égal à 1. Son ordre ne possède que 2 ou 3 comme facteur premier. On peut être plus précis :
- Tout groupe spécial orthogonal est d'ordre un diviseur de 24 :
- L'exposant de 3 de l'ordre d'un groupe spécial orthogonal d'un réseau de R3 ne peut être strictement supérieur à 1 :
- C'est une conséquence assez directe des théorèmes de Sylow. Ces théorèmes nous apprennent que tout groupe d'ordre 3p.b, où p et b désignent des entiers positifs et tel que b est un nombre premier, contient un groupe d'ordre 3p, appelé 3-sous-groupe maximal. Un tel groupe est un 3-groupe et possède des propriétés bien particulières. Son centre c'est-à-dire le sous-groupe des éléments qui commutent avec tous les éléments du 3-groupe n'est pas trivial.
- Considérons un 3-groupe G de plus de 3 éléments. Nous allons montrer qu'il contient un sous-groupe abélien de 9 éléments. Soit son centre contient strictement plus que 3 éléments, soit il existe un élément g, qui n'est pas dans le centre et le groupe engendré par le centre et g est un groupe abélien de strictement plus de trois éléments. On peut toujours extraire de ce sous-groupe un nouveau sous-groupe d'exactement 9 éléments.
- Le groupe spécial orthogonal ne peut contenir de sous-groupe abélien à 9 éléments. Un tel sous-groupe est soit isomorphe à C9 — le groupe cyclique à 9 éléments — mais aucun élément du groupe spécial orthogonal n'est d'ordre 9. Sinon il contient une copie du groupe C3 × C3. Or la théorie des représentations des groupes finis nous apprend qu'il n'existe pas de représentation fidèle, c'est-à-dire injective, d'un tel groupe en dimension 3. Le lemme, et le fait que le groupe spécial orthogonal ne puisse pas contenir un tel sous-groupe montre la proposition.
Recherchons maintenant le 2-groupe maximal d'un groupe spécial orthogonal.
- L'exposant de 2 de l'ordre d'un groupe spécial orthogonal ne peut être strictement supérieur à 3 :
- Le cas des groupes abéliens est relativement simple. Soit G un 2-sous-groupe abélien, sa décomposition en représentations irréductibles montre que la dimension nécessaire pour représenter C2 est 1 et qu'elle est égale à 2 pour Cn si n est strictement supérieur à 2. La valeur n ne peut dépasser 4 dans notre cas, car aucun élément du groupe spécial orthogonal ne possède un ordre supérieur à 4. G peut être isomorphe à C2, C2 × C2, C4 × C2 et C2 × C2 × C2 n'est pas possible car certains éléments seraient de déterminant −1. Le plus grand sous-groupe abélien est au maximum d'ordre 8 et si tel est son ordre, il est isomorphe à C4 × C2.
- Pour le cas non abélien, considérons son caractère, les seules valeurs possibles des images sont : soit 3, obtenu pour ω égal à 1, soit 1 obtenu pour ω égal à i ou −i. La valeur 3 ne peut être obtenue qu'une fois, la valeur 1 l'est nécessairement 2p − 1, si 2p désigne l'ordre de G. Une telle représentation ne peut être irréductible, le carré de la norme du caractère est en effet égal à 1/2p(9 + 2p − 1) qui ne peut être égal à 1 alors que c'est toujours le cas pour une représentation irréductible. Cette représentation est la somme directe de deux représentations irréductibles, l'une notée χ1 de degré 1, l'autre, χ2 de degré 2. Si χ2 n'était pas irréductible, la représentation se décomposerait en représentations irréductibles de degré 1, ce qui impose la commutativité du groupe, ce qui n'est pas le cas étudié. On remarque que les caractères χ1 et χ2 sont nécessairement à valeurs réelles car leur somme l'est, en effet :

- S'ils ne l'étaient pas, on aurait une combinaison linéaire nulle entre 4 caractères irréductibles distincts, ce qui ne se peut pas car les caractères irréductibles forment une famille libre (et même une base de l'espace des fonctions centrales).
- Le caractère χ2 est à valeurs réelles, mais les endomorphismes associés, maintenant sur un espace de dimension 2, ne sont pas nécessairement à déterminant positif. Cette fois ci, les valeurs possibles sont 2, −2 et 0. La trace 2 est nécessairement celle de l'identité et −2 celle de l'homothétie de rapport −1 car les valeurs propres d'un endomorphisme du groupe sont nécessairement de module égal à 1. On en déduit que les valeurs 2 et −2 ne sont atteintes qu'une unique fois. Le carré de la norme du caractère est maintenant égal à 1/2p(22 + 22) = 1. On en déduit que p est égal à 3 et l'ordre du groupe à 8. Le seul groupe non commutatif d'ordre 8 est le groupe diédral D8, dont on reconnaît le caractère d'une représentation irréductible et fidèle. Le terme fidèle signifie que la représentation est injective.
On a démontré que les plus larges 2-groupes sont les 2-groupes C4 × C2 et D8, deux groupes d'ordre 8 susceptibles d'être contenus dans un groupe spécial orthogonal d'un réseau de dimension 3. Le plus large 3-groupe est C3 et il n'existe pas d'autre p-groupe, ce qui démontre la proposition.
Représentations irréductibles de degré 3
Le principe de la démarche consiste à étudier dans un premier temps les groupes orthogonaux admettant une représentation irréductible, puis ceux ayant une représentation de degré 2, enfin ceux n'ayant que des représentations de degré 1. Pour plus de simplicité, on recherche d'abord uniquement le groupe spécial orthogonal et l'on se limite aux groupes n'ayant pas d'éléments d'ordre 6. Cette démarche met en évidence le groupe du cube. On pourrait utiliser uniquement les outils de l'algèbre linéaire, mais, pour autant d'effort, on ne trouverait que des résultats plus partiels[9].
Le groupe orthogonal possède une représentation naturelle. Un élément d'un tel groupe est une isométrie d'un réseau, qui se prolonge naturellement en une isométrie de ℝ3. On peut aussi le considérer comme une isométrie de ℂ3. Il existe deux manières de le faire. Soit on considère sa matrice dans la base canonique, elle peut aussi être vue comme la matrice d'une isométrie de ℂ3 exprimée dans la base canonique. Soit on étudie le produit tensoriel de ℂ par
ℝ3, qui est un ℂ-espace vectoriel de dimension 3 sur lequel s'étend naturellement l'isométrie du groupe orthogonal. On sait qu'une telle représentation est fidèle, c'est-à-dire qu'elle est injective. En effet, à une matrice donnée dans une base donnée, ne correspond qu'une application linéaire.
- Les seuls sous-groupes d'un groupe spécial orthogonal n'ayant pas d'élément d'ordre 6 et ayant une représentation irréductible de degré 3 sont S4 et A4 :
Ici A4 désigne le groupe alterné d'indice 4 à 12 éléments. Il correspond aux permutations d'un ensemble à 4 éléments ayant une signature positive. Le groupe A4 n'est jamais un groupe spécial orthogonal, ce que nous montrerons un peu plus loin.
- Si un sous-groupe d'un groupe spécial orthogonal admet une représentation irréductible de degré 3, son ordre est soit 12, soit 24 :
- Soit G le groupe étudié, g son ordre et φ une représentation irréductible de G. Les seules valeurs possibles de la trace des images de φ sont 3, 1, 0 et −1. En effet, les images de φ sont des rotations d'un angle particulier égal à kπ/3 ou kπ/4 avec k entier. L'angle nul correspond à l'identité, élément du groupe de trace 3. Les rotations d'angles π/3 et 4π/3 sont impossibles car le groupe n'a pas d'élément d'ordre 6. Les rotations d'angles 2π/3 et 4π/3 donnent pour trace 0. Celles d'un demi tour −1 et celle d'un quart de tour 1. Soit p1 (resp. p0 et p−1) le nombre d'isométries du groupe ayant une trace égale à 1 (resp. 0 et −1), il n'existe qu'un unique endomorphisme ayant une trace égale à 3, l'identité.
- On cherche une représentation irréductible φ ; cela impose comme contrainte que le carré de la norme de son caractère χφ soit égal à 1, soit encore : 9 + p1 + p−1 = g, l'ordre du groupe recherché. On sait aussi que g = 1 + p1 + p−1 + p0 et que le caractère χφ est orthogonal au caractère trivial χt, qui associe 1 à chaque élément, et donc 3 + p1 − p−1 = 0. On en déduit que p0 est égal à 8, p−1 au moins à 3. Enfin, on sait de g est un diviseur de 24.
- Ces différentes équations n'ont que deux solutions, soit p1 est égal à 6, p−1 à 9 et p0 à 8, soit p1 est égal à 0, p−1 à 3 et p0 à 8. Ce qui démontre bien la proposition, en effet dans le premier cas g = 1 + 9 + 8 + 6 = 24 et dans le deuxième g = 1 + 8 + 3 = 12.
En fait, la démonstration nous apporte plus d'informations. La signature 3 impose un élément d'ordre 1, le groupe ne contient qu'une unité (ce qui n'est pas étonnant, cette propriété est vraie pour tous les groupes), 9 isométries de trace −1 impose qu'il existe 9 éléments d'ordre 2, la trace 0 indique 8 éléments d'ordre 3 et la trace 1, 6 éléments d'ordre 4. Ces résultats s'appliquent pour le groupe à 24 éléments.
On se concentre maintenant sur un groupe G à 24 éléments ; l'objectif est de montrer que ce groupe est nécessairement celui du cube :
- Le groupe G contient un sous-groupe distingué d'ordre 12 :
- La représentation régulière de G est de degré 24 ; elle contient 3 copies de la représentation étudiée, qui occupent 9 dimensions et la représentation triviale, qui en occupe une. Il en reste 14, qui peuvent être utilisées par des représentations de degré 1, 2 ou 3. Analysons celles de degré 1 ; elles sont nécessairement associées à des sous-groupes cycliques, les seules valeurs possibles pour la longueur du cycle sont 2, 3 et 4. La valeur 3 est impossible, en effet, si 3 était une valeur possible, il existerait un morphisme du groupe G surjectif dans C3 et G serait le produit semi-direct d'un sous-groupe d'ordre 8 et de C3. Les seuls morphismes de C3 dans le groupe des automorphismes d'un groupe d'ordre 8 sont les morphismes triviaux, le produit serait donc direct. Comme G n'est pas abélien — car il dispose d'une représentation irréductible de degré 3 — la seule valeur du groupe possible est D8, le seul groupe non commutatif d'ordre 8, or le produit direct de D8 et C3 contient un élément d'ordre 12, ce que ne contient pas G.
- Une analyse de dimension montre que G ne contient pas les représentations de C4. En effet, s'il les contenait, ces représentations occuperaient, en plus de la représentation triviale, trois dimensions, il resterait alors 11 dimensions à remplir avec des représentations d'ordre 2 qui occupent 4 dimensions chacune et celles d'ordre 3 qui en occupent 9, ce qui est impossible. Il ne reste comme choix que l'usage de la deuxième représentation σ de C2, différente de la triviale. Les représentations d'ordre 1 : la triviale et σ, occupent deux dimensions, une de degré 2 porte à 6 les dimensions occupées et deux représentations de degré 3 prennent les 18 restantes.
- On en déduit qu'il existe une représentation non triviale et de dimension 1, associée au groupe cyclique d'ordre 2. Elle représente la signature, le noyau de cette représentation est d'ordre 12 et est distingué.
Nous ne sommes plus très loin de pouvoir identifier G à S4. Nous pouvons identifier les 4 classes de conjugaison de G, la classe de l'unité, celle d'éléments d'ordre 2, d'ordre 3 et d'ordre 4 ou 2. Il en existe en fait 5. De plus nous connaissons 3 représentations irréductibles, la triviale t, la signature σ et une irréductible φ, dont les déterminants sont tous égaux à 1.
- Il n'existe qu'un groupe à 24 éléments susceptible d'être un groupe spécial orthogonal, S4, dont la table des caractères est la suivante :
| Car. irr. | 1 | (ab) | (abc) | (ab)(cd) | (abcd) |
| Nb d'él | 1 | 6 | 8 | 3 | 6 |
| χt | 1 | 1 | 1 | 1 | 1 |
| χσ | 1 | −1 | 1 | 1 | −1 |
| χθ | 2 | 0 | −1 | 2 | 0 |
| χφ | 3 | 1 | 0 | −1 | −1 |
| χφσ | 3 | -1 | 0 | −1 | 1 |
|
Les valeurs de la table ne sont pas données sur les éléments mais sur les classes de conjugaison dont le cardinal est donné en deuxième ligne. En effet, un caractère est toujours constant sur une classe de conjugaison. La représentation φσ correspond à celle qui, à un élément h du groupe, associe l'isométrie (−1)σ(h) φ(h). La représentation θ reste à déterminer.
- Les éléments de G ayant une image égale 0 ou 3 par χφ sont d'ordre impairs, respectivement 1 et 3, il suffit de multiplier par elles-mêmes leurs matrices pour s'en rendre compte. La représentation associée à σ est égale à 1 pour ces valeurs. La valeur 1 est encore atteinte 3 fois et la valeur −1, 12 fois pour les éléments de G qui ont 1 et −1 comme image par χφ. On sait en effet qu'il existe 12 images de valeur 1 et 12 de valeur −1. On note p (resp. q) le nombre des éléments du groupe ayant pour image par χφ 1 et par χσ 1 et (resp. −1). De même, on note r (resp. s) le nombre des éléments du groupe ayant pour image par χφ −1 et par χσ 1 et (resp. −1). On obtient les égalités :
 .
.
- Ces quatre équations sont liées ; la somme des deux premières est égale à celle des deux dernières, ce qui ne permet pas une résolution directe. Néanmoins, l'analyse conduisant à l'existence d'un sous-groupe d'ordre 12 montre qu'il existe 5 représentations irréductibles, donc 5 classes de conjugaison. Or l'image réciproque de −1 par χφ contient des éléments d'ordre 2 et 4, elle contient donc deux classes. On en déduit que, soit p, soit q est nul et que l'autre valeur est égale à 6. L'égalité p + r = 3 montre que la seule solution positive du système est p = 0, on en déduit q = 6, r = 3 et s = 6. En multipliant χφ par χσ, on obtient un nouveau caractère irréductible, soit maintenant 4 sur les cinq recherchés. La combinaison linéaire des caractères irréductibles avec comme coefficients leur dimension donne le caractère de la représentation régulière, ce qui permet de trouver le dernier caractère, noté ici χθ.
- Il est temps de conclure. Le groupe G recherché possède pour table des caractères celle de S4, ce qui montre que les deux groupes sont isomorphes.
Les isométries du groupe G correspondent à la représentation φ, car la représentation φσ possède des isométries de déterminants négatifs. Nous connaissons ainsi exactement les éléments du groupe spécial orthogonal. Ce groupe ne peut en effet être un sous-groupe, car nous savons déjà qu'il ne peut exister de groupe orthogonal d'ordre strictement supérieur à celui de G.
Analysons maintenant le deuxième cas, celui où le groupe G contient 12 éléments.
- Le seul sous-groupe d'un groupe spécial orthogonal, d'ordre 12 et admettant une représentation irréductible de degré 3, est isomorphe à A4 :
Il possède, comme table des caractères :
| Car. irr. | 1 | (ab)(cd) | (abc)1 | (abc)2 |
| Nb d'él | 1 | 3 | 4 | 4 |
| χt | 1 | 1 | 1 | 1 |
| χj | 1 | 1 | j | j |
| χj | 1 | 1 | j | j |
| χψ | 3 | −1 | 0 | 0 |
|
- Le groupe G est maintenant d'ordre 12, et le caractère de la représentation associée au groupe spécial orthogonal ψ prend 1 fois la valeur 3, 8 fois la valeur 0 et 3 fois à valeur −1. En plus du caractère trivial χt, il ne reste que deux dimensions à trouver pour comprendre la représentation régulière de G. Ces deux dimensions ne peuvent correspondre qu'à des représentations de dimension 1, car une représentation de dimension 2 prend déjà 4 dimensions. Le seul sous-groupe cyclique offrant deux dimensions supplémentaires est C3 ; les deux caractères manquants prennent donc les valeurs j et son conjugué. On connaît maintenant une partition du groupe en 3 sous-ensembles, il en faut 4 pour connaître toutes les classes de conjugaison. La seule solution pour préserver l'orthogonalité des caractères est de diviser en deux parties égales l'image réciproque de 0 par χφ. On obtient la table des caractères attendue, correspondant au groupe alterné d'indice 4[10]. On sait maintenant qu'un groupe spécial orthogonal ayant une représentation irréductible de dimension 3 sans élément d'ordre 6 est soit le groupe S4, soit le groupe A4.
Il reste encore 3 étapes à franchir pour terminer l'étude des groupes orthogonaux de cette nature. Montrer que ni les groupes contenant un éléments d'ordre 6 ni A4 ne sont susceptibles n'être des groupes spéciaux orthogonaux, déterminer le groupe orthogonal d'un réseau ayant pour groupe spécial orthogonal S4 et caractériser les géométries d'un réseau ayant ce groupe pour ensemble d'isométries. On va procéder dans l'ordre inverse. Tout d'abord déterminer la géométrie d'un réseau contenant comme isométries directes (de déterminant 1) un groupe isomorphe à S4 et trouver trois solutions qui ont toutes S4 × C2 comme groupe orthogonal, à un isomorphisme près. Il sera alors temps de traiter le cas de l'existence d'un élément d'ordre 6.
- Il n'existe, à un isomorphisme près, que trois réseaux ayant un groupe orthogonal contenant un sous-groupe isomorphe à A4. Ils ont tous un groupe spécial orthogonal isomorphe à S4 :
Cette proposition permet de faire d'une pierre deux coups. Une fois les trois géométries explicitées, il sera fort simple de montrer que le groupe orthogonal est toujours celui des isométries du cube, d'ordre 48. Il n'existe qu'une représentation fidèle de dimension 3 du groupe A4 ; on en conclut que l'on connaît, à une isométrie près, exactement ces éléments du groupe orthogonal. Quitte à appliquer une rotation, il est toujours possible de choisir comme axes principaux de symétries ceux dirigés par i, j et k, la base canonique de ℝ3. Le groupe est engendré par les isométries composées des permutations des trois éléments de la base, sans en laisser aucun invariant, par les isométries qui changent de signe les coordonnées. Les seules isométries présentes dans le groupe A4 sont celles de déterminant 1. On peut les construire à l'aide des générateurs proposés dans l'article Représentations du groupe symétrique ; les isométries correspondent à la représentation notée φ1. Le groupe alterné est composé des isométries de cette représentation ayant une signature positive. On dispose ainsi de la représentation matricielle dans la base canonique.
- Un réseau ayant un groupe orthogonal contenant un sous-groupe isomorphe à A4 est l'image par la composée d'une rotation et d'une homothétie d'un sous-réseau de ℤ3 :
- Chaque axe principal contient des éléments du réseau. Montrons-le pour l'axe dirigé par i ; la démonstration serait la même pour j et k. Remarquons dans un premier temps que la rotation, d'axe dirigé par i et d'un demi tour, est un élément de A4. Pour s'en persuader, il est possible de calculer la matrice de la représentation de la permutation (ab)(cd). Soit α un élément non nul du réseau ayant pour coordonnées dans la base canonique (x, y, z), le point (x, −y, −z) est élément du réseau car image de α par la rotation d'un demi tour. La somme de ces deux points est encore un élément du réseau, ayant une composante nulle sur j et k.
- Il est temps de trouver le réseau contenant λ. Soit a la plus petite valeur strictement positive touchée par la forme linéaire définie par le produit scalaire associé à i. L'existence d'une telle valeur est établie dans la démonstration de l'existence d'une base dans le cas général. Il suffit de remarquer qu'il existe un sous-réseau de dimension 2 dans le plan dirigé par j et k. Les rotations images de A4 assurent que les coefficients définis de la même manière pour les axes j et k sont égaux à a. Il suffit pour s'en rendre compte de construire la matrice associée à la composée des permutations (ab) et (bc). Au signe près, elle transforme a.i en a.j puis en a.k. Considérons le réseau des points de ℝ3 de coordonnées des multiples de a, à coefficients dans ℤ, dans la base canonique. Ce réseau contient nécessairement λ et, à une homothétie de rapport a−1 près, est égal à ℤ3.
- On remarque que ℤ3 est stable par les rotations d'un tiers de tour et d'axes ceux dirigés par ±i ± j ± k. Comme l'image de A4 par la représentation est engendrée par ces huit rotations, le réseau est bien stable par l'action de la représentation du groupe A4. Ce qui termine la démonstration.
On dispose maintenant d'au moins un réseau ayant un sous-groupe isomorphe à A4 dans le groupe orthogonal. Il reste encore un peu de travail pour trouver les autres, s'assurer de l'exhaustivité de la liste et montrer que le groupe orthogonal est toujours égal à celui du cube.
La démonstration précédente nous simplifie la vie. Il ne devient nécessaire que d'étudier les sous-réseaux de ℤ3. À un isomorphisme près, ce sont les seuls qui contiennent une représentation irréductible de dimension 3, au détail près des groupes orthogonaux contenant un élément d'ordre 6, qui n'est toujours pas traité. L'étape suivante consiste à établir la liste des sous-réseaux stables par le sous-groupe isomorphe à A4 dans ℤ3. Pour ce faire, on considère un point non nul du réseau et on le note (a, b, c), sachant que les coordonnées sont entières. On fait agir le sous-groupe isomorphe à A4 sur cet élément, c'est-à-dire que l'on applique à cet élément différentes isométries du sous-groupe. En utilisant la stabilité de l'addition et de la soustraction du groupe, on obtient, à une homothétie près, trois familles de réseau.
Si on allait un peu plus loin, on montrerait que le réseau engendré par (1,1,0) est isomorphe à celui engendré par (1,1,1). La séparation de ces deux réseaux est donc un peu conventionnelle. Elle existe car elle a du sens en cristallographie.
- Tout sous-réseau de ℤ3 et de groupe orthogonal contenant un sous-groupe isomorphe à A4, est homothétique à l'un des trois réseaux, engendrés soit par (1,0,0), soit par (1,1,0) soit par (1,1,1) :
- On a vu que le changement de signe d'une coordonnée ne modifie pas l'appartenance au réseau d'un point. On doit donc supposer a, b et c positifs. S'ils sont tous trois égaux, le sous-réseau est engendré par a.(1,1,1) et la proposition est démontré. Il en est de même si deux coordonnées sont égales et que la troisième est nulle ou si deux coordonnées sont nulles. On suppose que l'on est dans le dernier cas, les trois coordonnées sont distinctes deux à deux et différentes de 0. Pour fixer les idées, on suppose que a est la plus grande et c la plus petite.
- Les calculs du paragraphe précédent montrent que le point (0, 0, 2c), puis (2c, 0, 0) puis enfin (|a − 2c|, b, c) sont encore des points du sous-réseau. On a pu strictement réduire la plus grande coordonnée. On peut réitérer cet algorithme jusqu'à ce que la première coordonnée soit égale à la dernière ou soit nulle.
- On peut ainsi supposer que le point s'écrit (c, b, c) ou (0, b, c), s'il n'est pas l'image par une homothétie d'un des trois points cités dans l'énoncé. On réitère le même algorithme, cette fois sur b et c. On obtient un point de la forme c(1, 1, 1) ou c (0, 1, 1) ou encore c(0, 0, 1). Il est ensuite possible de permuter l'unique 1 (resp. 0) ou en première (resp. dernière) position pour les deux derniers cas. On a bien 3 réseaux, à une homothétie de rapport c−1 près.
Nous sommes passés de l'étude de tous les réseaux dont le groupe orthogonal contient un sous-groupe isomorphe à A4, à ceux de ℤ3 puis à trois cas particuliers. Il suffit de déterminer le groupe orthogonal de ces trois réseaux pour conclure le cas où il n'existe pas d'éléments d'ordre 6 dans le groupe.
- Tout réseau de groupe orthogonal contenant un sous-groupe isomorphe à A4 possède un groupe orthogonal isomorphe au groupe S4 × C2 :
- Le cas le plus simple est celui contenant i = (1, 0, 0) ; il existe dans le groupe isomorphe à A4 une isométrie dont l'image de i est −k et l'image de −k est j ce qui montre que le réseau est égal à ℤ3, Il est simple de vérifier que ce réseau est stable par les trois générateurs du groupe correspondant aux rotations image de (abcd), (adbc) et (acdb). Le réseau est stable par trois isométries générant tout le groupe S4, le groupe orthogonal contient donc S4. On raisonne exactement de même pour les trois autres cas pour trouver un résultat analogue.
- Ce groupe est le noyau du morphisme de groupes qui à un élément associe son déterminant. Il existe au moins un élément du groupe de déterminant égal à −1, l'opposé de l'identité. Le morphisme divise le groupe en deux classes, le noyau et une autre contenant l'opposé de l'identité. Deux classes de cette nature ont nécessairement le même cardinal, le groupe orthogonal est d'ordre 48. Considérons maintenant le morphisme de S4 × C2 qui à (h, ε ) associe ε.φ(h). La valeur ε est égale à ±1 et φ désigne la représentation de S4 à valeurs dans le groupe spécial orthogonal. Cette application est clairement injective : un élément du noyau est composé d'un membre h du groupe ayant une image égale à plus ou moins l'identité or le caractère de la représentation montre qu'il n'existe qu'un élément de cette nature, l'identité. Le morphisme considéré étant injectif et entre deux groupes ayant même cardinal, il est nécessairement bijectif, ce qui termine la démonstration.
Il ne reste plus qu'un cas à traiter :
- Aucun groupe orthogonal contenant un élément d'ordre 6 ne possède de représentation irréductible de degré 3 :
.jpg.webp)
Fig. 20.
.jpg.webp)
Fig. 21.
- On utilise ici une technique géométrique. On cherche un plan Δ le plus invariant possible par les isométries du groupe orthogonal G. Soit Θ une rotation d'ordre 6, c'est-à-dire d'un angle de π/3. Une telle rotation existe, il existe un élément d'ordre 6, soit cet élément, soit son opposé est une rotation et ces deux isométries sont dans G. La rotation Θ laisse un unique plan invariant, on suppose donc que Δ est celui-là. Soit α un point non nul du réseau dans le plan Δ et de norme minimale. La même technique ayant servi à montrer que tout plan invariant par le groupe orthogonal contient un sous-réseau de dimension 2, permet de montrer que le plan Δ contient un sous-réseau de dimension 2 et que α existe bien. Les images de α par les itérés de Θ forment un hexagone, comme sur la figure 20. On note β l'image de α par Θ. L'objectif est de montrer que Δ est bien stable par tous les éléments de G. Pour cela on considère Σ une rotation qui ne laisse pas le plan invariant. Soit l'image de α par Σ, soit celle de β n'est pas dans Δ. Quitte à modifier les notations d'un sixième de tour, on peut toujours supposer que le point γ, égal à Σ(α), n'est pas dans le plan.
- Si le point γ est orthogonal à Δ, alors Σ n'est pas dans le groupe orthogonal. La figure 20 explique tout. La rotation Σ possède un axe orthogonal à α et γ. C'est une rotation d'un quart de tour. Considérons les coordonnées du point Σ(β). Si Σ était dans le groupe orthogonal, le triplet (α, β, γ) formerait une base du réseau car ils sont de normes minimales et forment une famille libre. Le point Σ(β) serait élément du réseau et aurait donc des coordonnées entières dans la base précédente. Or sa coordonnée sur le vecteur γ est égale à 1/2, qui n'est pas un entier.
- Si le point γ est n'est pas orthogonal à Δ, alors Σ n'est pas dans le groupe orthogonal. Cette fois-ci, la figure 21 explique tout. Le point γ n'est pas dans Δ, sa projection orthogonale sur ce plan est de norme strictement plus petite que celle de α. Considérons maintenant la différence δ entre γ et Θ(γ). Cette différence δ, de norme égale à la projection orthogonale de γ sur Δ est strictement plus petite que celle de α, elle ne peut appartenir au réseau. En effet, sur Δ il n'existe pas d'autre vecteur que le vecteur nul, à la fois élément du réseau et de norme strictement plus petite que celle de α. Or si Σ était dans le groupe orthogonal, δ serait un point du réseau et de Δ.
- En résumé, toutes les rotations du groupe orthogonal laissent Δ globalement invariant. Toutes les isométries laissent ce plan invariant, car si une isométrie n'est pas une rotation, son opposé l'est et si son opposé ne laisse pas le plan invariant, l'isométrie ne le laisse pas non plus. Le théorème de Maschke montre que cela impose à la représentation de ne pas être irréductible.
On peut maintenant énoncer le théorème de cette boite de dialogue.
- Le seul groupe orthogonal ayant une représentation irréductible de dimension 3 est isomorphe au groupe du cube S4 × C2. Il s'obtient avec trois types de réseau, tous sous-réseaux de ℤ3, ces sous réseaux sont engendrés respectivement par (1, 0, 0), (1, 1, 0) et (1, 1, 1) :
Les représentations d'un groupe fini ont été bien utiles. Montrer l'existence d'un réseau ayant un groupe orthogonal isomorphe à celui du cube devient plus rapide et plus simple, ce que l'on peut vérifier avec la référence qui procède autrement. Mais ce n'est pas là que réside la réelle difficulté. Elle tient à l'exhaustivité de l'analyse. On cherche tous les groupes orthogonaux. Le fait que l'on sache que les autres groupes n'ont pas de représentation irréductible de degré 3 et donc qu'il existe plan invariant par toutes les isométries du groupe orthogonal, ramène essentiellement la suite de l'étude à celle des groupes orthogonaux de réseaux de dimension 2. Or cette étude est déjà faite.
Autres représentations
On suppose maintenant que le groupe orthogonal G admet une représentation irréductible de dimension 2, mais pas de dimension 3, le cas étant déjà traité. Le groupe n'est pas abélien car les seules représentations irréductibles d'un groupe abélien sont de dimension 1. Les représentations sont, en effet, considérées sur les complexes. Le groupe G est une représentation de lui-même, cette représentation admet nécessairement un espace stable de dimension 2, qui est peut-être complexe. Son orthogonal est aussi un sous-espace stable pour tous les éléments de G, cette fois de dimension 1. Le caractère, correspondant au rapport de l'homothétie qu'est la restriction d'une isométrie de G sur cet espace de dimension 1, est toujours réel. Cette propriété est démontrée dans l'étude sur l'ordre du groupe. Le sous-espace de dimension 1 est donc réel et par voie de conséquence celui de dimension 2 aussi. Nous savons maintenant qu'il existe un plan Δ de ℝ3 stable par toute isométrie de G et que son orthogonal est aussi stable et donc est composé de vecteurs propres pour tout élément de G. La seule valeur propre pour une isométrie réelle est ±1. Comme toute isométrie de G a son opposé aussi dans G, on en déduit que 1 est valeur propre sur l'orthogonal de Δ pour la moitié des éléments de G et −1 pour l'autre. Une autre remarque simplifie les démonstrations :
- L'intersection de Δ et du réseau est un sous-réseau de dimension 2 :
- Soit Σ une isométrie de G de valeur propre 1 sur l'orthogonal de Δ et λ un élément du réseau tel que Σ(λ) soit différent de λ. Les projections orthogonales de Σ(λ) et de λ sur l'orthogonal de Δ sont égales ; on en déduit que Σ(λ) − λ est un élément de Δ. Un élément de Δ ne peut être vecteur propre pour toutes les isométries de G, sinon l'espace vectoriel engendré par cet élément et l'orthogonal de Δ seraient deux espaces stables de ℝ3 par tout élément de G. L'orthogonal de ces deux espaces en serait un troisième et toutes les isométries de G seraient diagonalisables dans une même base, ce qui implique la commutativité du groupe G, contraire aux hypothèses. L'image de Σ(λ) − λ par une isométrie de G n'ayant pas ce vecteur pour vecteur propre fournit un deuxième vecteur non colinéaire à Σ(λ) − λ et aussi dans Δ. Ces deux vecteurs engendrent un sous-réseau de dimension 2 à l'intérieur de Δ.
La structure des réseaux ayant un groupe orthogonal non commutatif commence à se dessiner. Le réseau contient un sous-réseau Δ de dimension 2 tel que le groupe orthogonal de ce sous-réseau soit non commutatif. Sur l'orthogonal de Δ, la moitié du groupe se comporte comme l'identité et l'autre moitié comme son opposé. Une dernière remarque est utile : un groupe ne comportant que des éléments d'ordre 2 (sauf l'élément neutre) est commutatif.
On peut maintenant lister les différents groupes orthogonaux non commutatifs. On peut les diviser en deux parties, ceux qui contiennent un élément d'ordre 3 et ceux qui contiennent un élément d'ordre 4.
- Il existe trois groupes orthogonaux non commutatifs et différents du groupe du cube : D12 × C2, D12 et D8 × C2 :
Commençons par l'ordre 3.
- À l'exception du groupe du cube, il existe exactement deux groupes orthogonaux contenant un élément d'ordre 3 : D12 × C2 et D12 :
- Considérons une rotation d'ordre 3 ; son axe est nécessairement l'orthogonal de Δ car cette rotation n'a pas d'autre droite propre. Soit α un élément non nul de Δ et de plus petite norme ; l'étude du réseau hexagonal en dimension 2 montre que les images de α par toutes les rotations d'un angle kπ/3 sont dans Δ. Comme précédemment, on note β l'image de α par la rotation d'angle π/3. Il ne reste plus qu'à déterminer γ, un point non nul du réseau, de norme minimale et en dehors de Δ, pour connaître exactement la structure du réseau et son groupe orthogonal G. Comme γ est de norme minimale, sa projection orthogonale sur Δ est à l'intérieur de l'hexagone de rayon la moitié de la norme de α. Sinon, en retranchant soit ±α, soit ±β, on obtiendrait un élément du réseau hors de Δ et de norme strictement plus petite que celle de γ.
- Si le groupe contient une rotation Θ d'ordre 6, G est isomorphe à A2 × C2 et γ est orthogonal au plan Δ. En effet, le raisonnement utilisé pour montrer qu'aucune représentation irréductible de degré 3 ne contient d'élément d'ordre 6 montre que le vecteur γ − Θ(γ) est un élément de Δ de norme strictement plus petite que celle de α. Il n'en existe qu'un : le vecteur nul. Dire que le vecteur γ − Θ(γ) est nul revient à dire que γ fait partie des vecteurs propres de Θ, qui sont tous sur l'axe orthogonal à Δ. Le groupe orthogonal du réseau Δ est isomorphe à D12 d'après les résultats précédents. Les seuls prolongements de ces isométries sont ceux obtenus en donnant, pour image de γ, ±γ. On obtient bien un groupe isomorphe à D12 × C2.
_sym%C3%A9trie_hexagonale_(2).jpg.webp)
Fig. 22. Il n'existe qu'une position possible, pour le point σ, à un angle de π/3 près.
- Si le groupe ne contient pas de rotation Θ d'ordre 6, il contient au moins Θ2 une rotation d'angle 2π/3, car, par hypothèse, il existe un élément d'ordre 3. Pour comprendre la géométrie du réseau, il est nécessaire de localiser γ. On note δ un vecteur non nul du réseau de norme minimale et orthogonal au plan Δ. Il existe bien ; en effet, soit λ un élément du réseau en dehors de Δ, le vecteur λ + Θ2(λ) + Θ4(λ) du réseau est non nul et orthogonal au plan Δ. La famille (α, β, δ) forme une base de l'espace vectoriel ℝ3, soit (a, b, c) les coordonnées de γ dans cette base. La projection orthogonale σ de γ dans Δ est dans l'un des six triangles équilatéraux du réseau dont l'un des sommets est l'origine et dont les côtés sont d'une longueur égale à la norme de α. Quitte à modifier le choix de l'un des six vecteurs de norme minimale que l'on a appelé α, on peut supposer que σ est dans le triangle équilatéral de sommet l'origine, α et β, ce qui signifie que a et b sont positifs et inférieurs à 1. On sait par ailleurs que a et b sont inférieurs à 1/2. L'image Θ2(σ) est un point qui se trouve dans le triangle de sommets : l'origine, −α et β − α. Cette situation est illustrée sur la figure 22. Comme γ − σ est dans l'axe de la rotation Θ, le point σ − Θ2(σ) est un point du réseau. Comme les coordonnées de σ dans la base (α, β) sont inférieures à 1/2, la seule valeur possible pour cette différence est α, ce qui se conçoit aisément sur la figure 22. L'équation Θ2(σ) = σ − α n'admet qu'une unique solution, donnée par σ = 1/3(α + β). On en déduit qu'un vecteur non nul de plus petite norme, élément de l'axe orthogonal à Δ, est 3γ − α − β et le coefficient c est égal à 1/3. Autrement dit, γ = 1/3(α + β + δ).
- Une fois la géométrie du réseau établie, il est temps d'analyser son groupe orthogonal. Chaque élément du groupe orthogonal du réseau du plan Δ peut être prolongé de deux manières différentes en une isométrie de ℝ3 : celle qui transforme δ en δ et l'autre dont l'image de δ est −δ. Il est nécessaire vérifier s'il existe des prolongements laissant invariant le réseau. Ce travail n'est nécessaire uniquement sur des générateurs du groupe orthogonal du plan, on en considère deux, Θ et Σ la réflexion laissant invariant α. Le projeté orthogonal de γ sur Δ a pour image par Θ le point Θ(σ), encore égal à −Θ4(σ), c'est-à-dire le projeté orthogonal de β − γ. Il existe un unique prolongement de Θ en une isométrie laissant invariant le réseau de dimension 3 : celui qui à γ associe β − γ. L'image par Σ du projeté orthogonal de γ sur Δ est égale à Θ−1(σ) ou encore à −Θ2(σ), c'est-à-dire au projeté orthogonal de α − γ. Il existe un unique prolongement de Σ en une isométrie laissant invariant le réseau de dimension 3. Le groupe orthogonal contient au moins autant d'éléments que son équivalent du réseau de dimension 2. Réciproquement, la restriction d'une isométrie de G au plan Δ est un élément du groupe orthogonal du réseau de dimension 2, car Δ est stable par toutes les isométries de G. Il y a donc au moins autant d'éléments dans le groupe orthogonal du réseau de dimension 2 que dans G. L'application de G dans le groupe orthogonal du réseau de Δ est un isomorphisme de groupes. On sait donc que G est isomorphe à D12.
- À l'exception du groupe du cube, il existe un unique groupe orthogonal contenant un élément d'ordre 4 : D8 × C2 :
- L'analyse commence comme la précédente ; Δ est le plan orthogonal à l'axe de Θ, une rotation d'ordre 4. Le point α non nul du réseau et de Δ est de norme minimale et β est égal à Θ(α). Enfin, γ est un vecteur du réseau hors de Δ et de plus petite norme. Comme précédemment, si γ est orthogonal à Δ, le groupe G est isomorphe au produit du groupe orthogonal du réseau de Δ et de C2. Les résultats précédents montrent que ce groupe est isomorphe à D8 × C2.
- On suppose maintenant que γ n'est pas dans l'orthogonal de Δ et l'on trouve que son projeté σ est égal à (α + β)/2 pour que la rotation Θ laisse stable le réseau. Si δ désigne le vecteur non nul du réseau, orthogonal à Δ, de norme minimale et de même sens que γ, on trouve que γ = (α + β + δ)/2. Cette fois-ci, la réflexion de γ sur le plan Δ est égale à (α + β − δ)/2 soit encore α + β − γ. La réflexion est élément du groupe orthogonal G. Même dans cette configuration, il existe deux manières de prolonger une isométrie laissant invariant l'intersection du réseau et de Δ. Le groupe G est encore isomorphe à D8 × C2.
Il reste encore à traiter le cas des groupes orthogonaux abéliens. Il est particulièrement aisé, sachant que les groupes non encore traités ne contiennent que des isométries involutives. Comme un groupe ne contenant que les isométries involutives est nécessairement abélien, sa structure s'établit de manière immédiate.
- Il existe trois groupes orthogonaux abéliens : C2 × C2 × C2, C2 × C2 et C2 :
Le groupe orthogonal est isomorphe à C2 × C2 × C2 si, et seulement si, il existe trois droites propres communes à tous les éléments de G. Un tel groupe s'obtient s'il existe une base orthogonale du réseau. Les autres géométries s'obtiennent en généralisant l'analyse menée en dimension 2 sur le groupe de Klein.
Le groupe orthogonal est isomorphe à C2 × C2 si, et seulement si, le réseau ne répond à aucune des géométries précédentes et qu'il existe une droite propre commune à tous les éléments du groupe orthogonal. Il s'obtient, par exemple, s'il existe une base dont l'un des vecteurs est orthogonal aux deux autres. Les autres géométries s'obtiennent à l'aide d'une démarche analogue à la précédente.
Si aucune des géométries précédentes ne correspond à celle du réseau, son groupe orthogonal ne contient que l'identité et son opposé, il est alors isomorphe à C2.
Dimensions supérieures
Plus la dimension grandit, plus la question s'avère délicate. On peut encore traiter le cas de la dimension 4 avec les mêmes outils que ceux de la dimension 3. Ensuite, si les méthodes sont essentiellement issues de la théorie des représentations d'un groupe fini, d'autres théorèmes s'avèrent de plus en plus nécessaires.
Ces groupes orthogonaux sont étudiés car, pour d'autres branches du savoir, ils ne manquent pas d'attraits. Ils permettent de représenter certains groupes finis et offrent de nombreuses méthodes pour les étudier. C'est ainsi que J. H. Conway trouve 3 parmi les derniers groupes manquants pour une classification complète des groupes finis[11]. Le réseau utilisé est de dimension 24 et porte le nom de Leech. Un autre cas célèbre est celui du groupe Monstre, le plus gros des 26 groupes sporadiques. Son existence était annoncée depuis une dizaine d'années avant sa construction[12]. Elle devait découler d'une représentation de degré 196 883, conjecturé et explicité sans l'aide d'ordinateur. Elle devrait clore la classification des groupes finis simples. Un réseau est utilisé.
D'autres branches des mathématiques font usage d'un réseau. L'étude des courbes elliptiques, développée au XIXe siècle demande l'analyse de réseau de dimension 2. Cette étude se généralise en dimension supérieure par la théorie des fonctions abéliennes.
Usages
Covolume
Une illustration de l'intérêt de la notion provient de la théorie algébrique des nombres, et plus spécifiquement de la géométrie arithmétique. Si K est une extension finie de degré n du corps ℚ, il est possible d'identifier l'anneau de ses entiers algébriques à un ℤ-module libre de dimension n. Une extension finie de ℚ est un ℚ-espace vectoriel de dimension finie et peut être vue comme un sous-corps de ℂ. Un entier algébrique est un nombre qui est racine d'un polynôme unitaire à coefficients dans ℤ. Un exemple simple est le corps des rationnels de Gauss, c'est-à-dire des nombres de la forme a + ib, où a et b sont des éléments de ℚ et i l'unité imaginaire. Les entiers algébriques de ce corps, appelés entiers de Gauss, sont les nombres de la forme a + ib où, cette fois-ci, a et b sont des éléments de ℤ. Les points du réseau sont représentés sur la figure 23 par les intersections du quadrillage bleu foncé.
Cette vision permet d'interpréter géométriquement de nombreuses situations d'arithmétique. On peut interpréter, par exemple, le fait que le quotient de l'anneau A par un sous-réseau M de même dimension (comme un idéal non nul), est fini et égal à la valeur absolue du déterminant d'une base de M dans une base de A. Cette propriété, valable pour n'importe quel anneau des entiers algébriques d'un corps quadratique ou plus généralement d'un corps de nombres, se démontre par un calcul élémentaire. Son interprétation géométrique consiste à dire que le nombre de points du réseau qui appartiennent à un domaine fondamental du sous-réseau est égal au volume de ce domaine fondamental, lorsqu'on considère une base de A comme orthonormée.

Fig. 24. Illustration de l'anneau A = ℤ[3√2] en tant que réseau.
La figure 23 illustre cette interprétation lorsque M est l'idéal principal engendré par l'entier algébrique α = 2 + i dans les entiers de Gauss, c'est-à-dire que les points du sous-réseau sont les produits de α par un entier de Gauss quelconque. Une base du réseau A étant B = (1, i), une base du sous-réseau M = αA est αB = (α, αi) = (2 + i, –1 + 2i). Ce sous-réseau est représenté par les points verts sur la figure. Une classe d'équivalence de l'anneau quotient est géométriquement représentée par un décalage du réseau vert et qui contient un point du quadrillage, par exemple une classe est illustrée par les points bleus. Chaque classe contient un représentant dans la zone rouge des vecteurs de coordonnées comprises dans l'intervalle [0, 1[ dans la base (2 + i, –1 + 2i). Le nombre d'entiers de Gauss (réseau représenté par le quadrillage bleu foncé) qui se trouvent dans ce domaine fondamental est égal à la valeur absolue du déterminant de la base αB de M dans la base B de A. Ce déterminant (toujours positif dans l'exemple des entiers de Gauss, mais parfois négatif dans d'autres anneaux d'entiers algébriques) est appelé la norme arithmétique de α. Un rapide calcul montre que la norme arithmétique d'un entier de Gauss a + ib est égale à a2 + b2. Dans l'exemple choisi, le nombre d'entiers de Gauss qui se trouvent dans le domaine fondamental est bien égal à 5, la norme de 2 + i.
La figure 24 illustre un exemple similaire en dimension 3. L'anneau (dont les points sont représentés par les petites billes) est ici ℤ[3√2], de base B = (1, 3√2, 3√4) considérée comme orthonormée, et l'idéal principal M (dont les points sont en rouge) est engendré par α = 2. Le domaine fondamental du sous-réseau M est le cube rouge, constitué des points dont les coordonnées dans la base 2B de M appartiennent à [0, 1[ (c'est-à-dire dont les coordonnées dans B appartiennent à [0, 2[). Son volume, égal à la norme de α, soit 23 = 8 (déterminant de l'homothétie de rapport 2 en dimension 3), est bien égal au nombre de points du réseau appartenant au cube rouge. Chaque classe du quotient A/M = A/(2A) est représentée par l'un de ces 8 points : si β est un point quelconque de A, il est congru, modulo 2A, au point dont les coordonnées sont les restes (0 ou 1) des divisions euclidiennes par 2 de celles de β.
Ce résultat est à rapprocher du théorème de Pick qui indique, en dimension 2, la relation entre le nombre de points du réseau contenu dans un polytope P dont les sommets sont des éléments du réseau et la surface du polytope. La généralisation en dimension n est obtenue à l'aide du polynôme d'Ehrhart.
Ensemble convexe
Fig. 26. Exemple de convexe traité par le théorème de Minkowski.
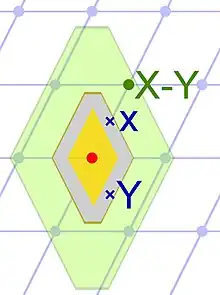
Fig. 25.
Le théorème de Minkowski indique qu'un convexe symétrique par rapport à l'origine et de volume supérieur à 2nV de ℝn rencontre nécessairement un point non nul du réseau de covolume V. La figure 26 représente, pour n = 3, un convexe symétrique par rapport à l'origine, son volume est donc inférieur à 8 fois le covolume, car il ne rencontre le réseau qu'au point d'origine.
L'article détaillé propose plusieurs démonstrations, dont l'une peut s'interpréter en termes de la représentation du domaine fondamental sous forme de tore. Le convexe C pour n = 2, illustré en vert sur la figure 25, est de volume supérieur à 4V ; l'image de ce convexe par une homothétie de rapport 1/2 est de volume supérieur à celui du tore. Cette configuration est illustrée sur la figure 25. La restriction du morphisme canonique de ℝn dans ℝn/Λ ne peut être injective, car sinon ℝn/Λ contiendrait un volume dont la mesure serait strictement supérieure à la sienne. Il existe donc deux points X et Y ayant même image par le morphisme, ou encore X – Y est élément de Λ. Or X et –Y sont éléments de (1/2)C et (X – Y)/2 l'est aussi, donc X – Y est élément de C. La zone où le morphisme n'est pas bijectif est indiquée en gris sur la figure 25. Son image par le morphisme est la zone grise du tore illustré dans le paragraphe (voir supra) sur le domaine fondamental.
Ce théorème est utilisé par exemple pour établir le théorème des unités de Dirichlet, élucidant la structure du groupe des unités d'un anneau d'entiers algébriques.
.jpg.webp)
_hexagone.jpg.webp)
_base.jpg.webp)
_existence_d'une_base_dim_2.jpg.webp)
_domaine_fondamental.jpg.webp)




_sym%C3%A9trie_hexagonale.jpg.webp)
_sym%C3%A9trie_tetragonale.jpg.webp)
_sym%C3%A9trie_orthorombique.jpg.webp)
_sym%C3%A9trie_orthorombique_(2).jpg.webp)





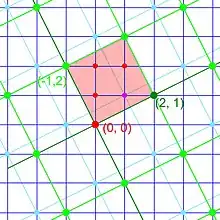





_existence_d'une_base.jpg.webp)








.jpg.webp)
.jpg.webp)
_sym%C3%A9trie_hexagonale_(2).jpg.webp)