NP-difficile

Un problème NP-difficile est, en théorie de la complexité, un problème appartenant à la classe NP-difficile, ce qui revient à dire qu'il est au moins aussi difficile que les problèmes les plus difficiles de la classe NP.

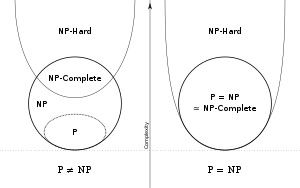
Mise en évidence d'un problème NP-difficile si Problème P ≟ NP.

Ainsi, un problème H est NP-difficile, si tout problème L de la classe NP peut être réduit en temps polynomial à H[1].

Si un problème NP-difficile est dans NP, alors c'est un problème NP-complet. Donc tous les problèmes NP-complets sont NP-difficiles.

Références

D. E. Knuth, « Postscript about NP-hard problems », ACM SIGACT News, vol. 6, n^o 2,‎ 1^er avril 1974, p. 15–16 (ISSN 0163-5700, DOI 10.1145/1008304.1008305, lire en ligne, consulté le 6 mars 2023)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.