Théorie de la complexité (informatique théorique)
La théorie de la complexité est le domaine des mathématiques, et plus précisément de l'informatique théorique, qui étudie formellement le temps de calcul, l'espace mémoire (et plus marginalement la taille d'un circuit, le nombre de processeurs, l'énergie consommée …) requis par un algorithme pour résoudre un problème algorithmique. Il s'agit donc d'étudier la difficulté intrinsèque des problèmes, de les organiser par classes de complexité et d'étudier les relations entre les classes de complexité.
Problèmes algorithmiques

Considérons l'exemple du problème du voyageur de commerce. La donnée du problème est un ensemble de villes et de distances séparant ces villes. L'objectif du problème est de trouver un plus court circuit qui passe une et une seule fois par toutes les villes. Il existe un problème de décision associé : étant donné un ensemble de villes, les distances entre villes et un entier k, déterminer s'il existe un circuit qui passe une et une seule fois par toutes les villes de longueur inférieure à k. Ainsi, on distingue deux types de problèmes.
- Les problèmes de décision posent une question dont la réponse est oui ou non ; dans le cas du problème du voyageur de commerce : existe-il oui ou non un circuit de longueur inférieure à k ?
- Les problèmes de recherche d'une solution comportent une question ou plutôt une injonction de la forme « renvoyer un élément tel que… » dont la réponse consiste à fournir un tel élément; dans le cas du problème du voyageur de commerce, exhiber un circuit de longueur minimale. Il s'agit donc d'un problème fonctionnel, et il sera donc catégorisé dans une classe fonctionnelle, par exemple FP si la solution est calculée en temps polynomial.
La théorie de la complexité étudie principalement (mais pas uniquement) les problèmes de décision.
Quelques exemples de problèmes de décision
Un exemple de problème de décision est :
« Étant donné un entier n, est-il premier ? » (PRIME)
Instances
Dans le cadre de la théorie de la complexité, la donnée d'un problème s'appelle une instance. Une instance du problème du voyageur de commerce est la donnée de villes et de distances séparant les villes. Comme on mesure la complexité en fonction de la taille d'une instance, la représentation (le codage) d'une instance joue un rôle important. Par exemple, un entier comme 13 peut être représenté en unaire (IIIIIIIIIIIII) ou en binaire (1101). En unaire, la taille de l'instance 13 est 13 et en binaire, la taille de l'instance est 4 (car il y a quatre chiffres dans 1101).
De la recherche à la décision
Un problème de recherche peut parfois être transformé en un problème de décision équivalent. Par exemple, le problème du voyageur de commerce qui cherche, dans un graphe dont les arêtes sont étiquetées par des coûts, à trouver un cycle de coût minimum, passant une fois par chaque sommet, peut s'énoncer en un problème de décision comme suit : Existe-t-il un cycle hamiltonien (passant une fois par chaque sommet) de coût inférieur à k (donné dans l'instance) ? L'équivalence de ces deux problèmes doit être démontrée, elle montre que la démonstration d'existence repose sur un argument constructif[1], c'est-à-dire, par exemple, dans le cas du voyageur de commerce, fournissant effectivement un cycle. Ceci n'est pas vrai en général : par exemple le problème PRIME ci-dessus est soluble en temps polynomial, mais aucune solution (algorithme) polynomiale n'est connue pour le problème de recherche associé : la factorisation, fournir les facteurs d'un nombre naturel.
Le problème de rechercher un cycle de coût minimum est équivalent au problème du voyageur de commerce, au sens où si l'on sait résoudre efficacement l'un, on sait aussi résoudre efficacement l'autre. Dans la suite de cet article, nous ne parlerons que de problèmes de décision, mais il existe une branche de la complexité dédiée aux problèmes fonctionnels.
Représentation d'un problème de décision
Si toute entrée est acceptée, autrement dit si le problème n'a pas de précondition, un problème de décision peut être vu comme l'ensemble des instances positives, c'est-à-dire les instances pour lesquelles la réponse est "oui". Par exemple, pour le problème de primalité, le problème de décision est l'ensemble des nombres premiers. Étant donné un codage des instances par des mots, on peut voir un problème de décision comme un langage formel : l'ensemble des mots qui représentent les instances positives.
Réponse algorithmique
Considérons à présent un algorithme qui résout le problème du voyageur de commerce. L'algorithme exécute des étapes élémentaires de calcul et le nombre d'étapes dépend de la taille de l'entrée. Pour le problème du voyageur de commerce, la taille de l'entrée est la quantité de mémoire nécessaire pour représenter les villes et les distances qui les séparent. Pour mesurer le temps d'exécution d'un algorithme, on définit la complexité en temps qui représente le nombre d'étapes qui sont nécessaires pour résoudre le problème pour une entrée de taille donnée.
Bien sûr, il existe de nombreux algorithmes qui résolvent le même problème. La théorie de la complexité s'attache à connaître la difficulté (ou la complexité) intrinsèque d'un problème algorithmique, c'est-à-dire celle de l'algorithme le plus efficace pour ce problème. On classifie les problèmes (et non pas les algorithmes) en termes de classes de complexité.
Dans chaque catégorie de problèmes ci-dessus, on dit qu'un problème a une réponse algorithmique si sa réponse peut être fournie par un algorithme. Un problème de décision — donc un problème dont la réponse est soit « oui » soit « non » — est décidable si sa réponse peut être fournie par un algorithme. De la même façon, on dit qu'un problème fonctionnel est calculable si l'élément solution peut être calculé par un algorithme. Il existe aussi des classes de complexité pour les problèmes non-décidables, comme celles de la hiérarchie arithmétique.
Pour les problèmes décidables, on cherche à évaluer les ressources – temps et espace mémoire – mobilisées pour obtenir algorithmiquement la réponse.
Complexité d'un problème algorithmique
La théorie de la complexité vise à savoir si la réponse à un problème peut être donnée très efficacement, efficacement ou au contraire être inatteignable en pratique, avec des niveaux intermédiaires de difficulté entre les deux extrêmes ; pour cela, elle se fonde sur une estimation — théorique — des temps de calcul et des besoins en mémoire informatique. Dans le but de mieux comprendre comment les problèmes se placent les uns par rapport aux autres, la théorie de la complexité établit des hiérarchies de difficulté entre les problèmes algorithmiques, dont les niveaux sont appelés des « classes de complexité ». Ces hiérarchies comportent des ramifications, suivant que l'on considère des calculs déterministes — l'état suivant du calcul est « déterminé » par l'état courant — ou non déterministes.
Modèles de calcul

L'analyse de la complexité est étroitement associée à un modèle de calcul. L'un des modèles de calcul les plus utilisés, car il permet de mesurer le temps de calcul et la mémoire utilisée, est celui de la machine de Turing proposé par Alan Turing en 1936. Un calcul est constitué d'étapes élémentaires. À chaque étape, la machine exécute une action élémentaire (changer d'état interne et déplacer la tête de lecture) en fonction de sa configuration courante (état interne et du symbole lu par la tête de lecture).
D'autres modèles de calcul qui permettent d'étudier la complexité existent :
- machines de Turing non-déterministes (il peut y avoir plusieurs choix possibles d'actions à effectuer dans une configuration donnée) ;
- machines de Turing alternantes ;
- machines de Turing probabilistes ;
- la machine RAM (Random Access Machine) ;
- les circuits booléens et les programmes straight-line ;
- les fonctions récursives, dues à Kleene ;
- le lambda-calcul ;
- les automates cellulaires ;
- la logique linéaire ;
- les pebble games.
Mesure de la complexité
Les ressources les plus classiques sont le temps et l'espace utilisés.
Généralement, on mesure la quantité de ressources (temps, espace, etc.) requis en fonction de la taille de l'entrée (instance). La façon dont cette taille est mesurée joue un rôle crucial dans l'évaluation de la complexité de l'algorithme. Par exemple, pour le problème de tester si un nombre entier naturel est premier, une instance est un nombre entier naturel. La taille d'un nombre entier naturel se mesure généralement par le nombre de chiffres (par exemple le nombre de bits si le nombre est représenté en binaire). Ainsi, le nombre 1 024 peut être représenté avec seulement onze chiffres binaires et quatre chiffres décimaux et donc sa taille est 11 ou 4 ; la taille d'un entier p vaut alors O(log(p)). La théorie de l'information montre qu'on ne peut diminuer la taille davantage. On mesure la quantité de ressources en fonction de cette taille, qui sera notée n. L'évaluation des ressources requises permet de répartir les problèmes dans des classes de complexité.
Pour les machines déterministes, on définit la classe TIME(t(n)) des problèmes qui peuvent être résolus en temps t(n), c'est-à-dire pour lesquels il existe au moins un algorithme sur une machine déterministe résolvant le problème en temps t(n). Le temps est le nombre de transitions sur machine de Turing ou le nombre d’opérations sur machine RAM. En fait, ce temps n'est pas une fonction précise, mais un ordre de grandeur. On parle aussi d'évaluation asymptotique. En particulier les constantes multiplicatives sont systématiquement ignorées grâce au théorème de speedup linéaire. Ainsi, pour un temps qui s'évalue par un polynôme, ce qui compte est le degré du polynôme. Si ce degré est 2, on dira que l'ordre de grandeur est en O(n²), que la complexité est quadratique et que le problème appartient à la classe TIME(n²).
D'autre mesures existent :
- nombre de communications (voir la théorie de la complexité de la communication) ;
- nombre de portes dans un circuit booléen ;
- profondeur d'un circuit booléen ;
- nombre d'alternations (voir machines alternantes).
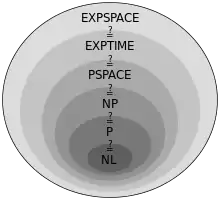
Classes de complexité
Une classe de complexité regroupe les problèmes de même complexité, souvent à une réduction polynomiale près. Les classes usuelles sont définies en utilisant les machines de Turing comme modèles de calcul et les ressources sont le temps et l'espace. Le tableau suivant donne quelques exemples de classes de complexité :
Problèmes ouverts en théorie de la complexité
Le problème ouvert P = NP
On a P ⊆ NP car tout algorithme déterministe est un cas particulier d'algorithme non déterministe. En revanche, la réciproque : NP ⊆ P, qui est la véritable difficulté de l'égalité P = NP, est un problème ouvert fondamental de l'informatique théorique. Il a été posé en 1970 indépendamment par Stephen Cook et Leonid Levin ; il fait partie des listes, établies en 2000, des problèmes du prix du millénaire et des problèmes de Smale.
La plupart des spécialistes conjecturent que les problèmes NP-complets ne sont pas résolubles en temps polynomial (donc, que P ≠ NP)[2]. Cela ne signifie pas pour autant que toute tentative de résoudre un problème NP-complet est vaine (voir la section « Résolution » de l'article sur la NP-complétude). Il existe de nombreuses approches (qui se sont finalement révélées irrémédiablement erronées) attaquant le problème P ≠ NP ; le spécialiste de la théorie de la complexité Gerhard Woeginger maintient une liste de ces erreurs[3].
La revendication de Vinay Deolalikar ()[4], travaillant aux HP Labs (en), d'une démonstration de P ≠ NP, a été la première à faire l'objet d'une attention relativement importante de nombreux mathématiciens et informaticiens de renom, que ce soit sous la forme d'échanges dans des blogs[5] - [6] - [7], de journaux en ligne ou sous la forme plus construite d'un projet d'étude collaborative en ligne (du type projet Polymath, tel que promu par les médaillés Fields Terence Tao et Tim Gowers). Cette étude collaborative donne la liste des points où l'approche de Vinay Deolalikar achoppe actuellement[8].
Autres problèmes ouverts
À l'instar du problème P = NP, on ne sait pas par exemple si :
- L = NL ?
- L = P ?
- NP = co-NP ?
- P = Pspace ?
- NP = Pspace ?
- Exptime = NExptime ?
Relation au coût énergétique
La complexité des opérations à réaliser a des conséquences sur leur déroulement concret, notamment la consommation d'énergie nécessaire à leur réalisation. Celle-ci peut varier considérablement suivant la performance des processus utilisés pour effectuer les calculs. En 1961, Rolf Landauer, de la société IBM, a proposé un modèle permettant d'estimer le coût en énergie minimal théorique en donnant une estimation du coût énergétique minimal de changement d'état d'un bit informatique[9]. En date de 2013, cette relation entre complexité et énergie, appelée principe de Landauer, est confirmée par les études expérimentales[10].
Histoire

Notes et références
- En fait, existence constructive et réponse par algorithme vont de pair, et cette exigence est tout à fait naturelle.
- [PDF] William I., Gasarch: Guest Column: the second P =?NP poll , SIGACT News 43(2): 53-77 (2012).
- (en) The P-versus-NP page, page personnelle de Gerhard J. Woeginger, de l'université technique d'Eindhoven.
- (en) Vinay Deolalikar, page personnelle aux HP Labs.
- (en) Putting my money where my mouth isn't, sur le blog de Scott Aaronson.
- (en) Gödel's lost letter and P=NP, sur le blog de Dick Lipton.
- (en) P ≠ NP, sur le blog de Greg Baker & Katrina G. Salvante.
- (en) Deolalikar P vs NP paper, sur le wiki du projet polymaths.
- « Tikalon Blog by Dev Gualtieri », Tikalon.com (consulté le )
- « Landauer Limit Demonstrated - IEEE Spectrum », Spectrum.ieee.org (consulté le )
Voir aussi
Articles connexes
- Complexité, article général sur la complexité
- Complexité de Kolmogorov
- Complexité descriptive
- Hiérarchie arithmétique
- Hiérarchie de Grzegorczyk
- Explosion combinatoire
- Machine de Turing non déterministe
- Réduction polynomiale
- Complexité des preuves, le domaine qui étudie la longueur des preuves des énoncés mathématiques selon les systèmes de preuves
Bibliographie
- Sylvain Perifel, Complexité algorithmique, Ellipses, , 432 p. (ISBN 9782729886929, lire en ligne)
- Olivier Carton, Langages formels, calculabilité et complexité, [détail de l’édition] (lire en ligne)
- (en) Sanjeev Arora et Boaz Barak, Computational Complexity : A Modern Approach, Cambridge University Press, (ISBN 0-521-42426-7)
- (en) Christos Papadimitriou, Computational Complexity, Addison-Wesley, (ISBN 978-0-201-53082-7)
- (en) Michael R. Garey et David S. Johnson, Computers and Intractability : A guide to the theory of NP-completeness, W.H. Freeman & Company, 1979 (ISBN 0-7167-1045-5)
- Richard Lassaigne et Michel de Rougemont, Logique et Complexité, Hermes, 1996 (ISBN 2-86601-496-0)
- Nicolas Hermann et Pierre Lescanne, Est-ce que P = NP ? Les Dossiers de La Recherche, 20:64–68, août-
Liens externes
- Notice dans un dictionnaire ou une encyclopédie généraliste :
- Ressource relative à la recherche :
- (en) Complexity Zoo consulté le
- (en) The Status of the P versus NP Problem : cet article, publié dans les Comm. of the ACM, a été cité par l'article New York Times ci-dessous.
- (en) « Prizes Aside, the P-NP Puzzler Has Consequences », The New York Times,