P (complexité)

Un problème est dans P s'il existe un algorithme qui le décide en temps polynomial. Citons :

• les restrictions 2SAT et HORNSAT du problème SAT sont dans P.
• Connexité dans un graphe : Un exemple de problème polynomial est celui de la connexité dans un graphe. Étant donné un graphe à n sommets (on considère que la taille de la donnée, donc du graphe, est son nombre de sommets), il s'agit de savoir si toutes les paires de sommets sont reliées par un chemin. Un algorithme de parcours en profondeur construit un arbre couvrant du graphe à partir d'un sommet. Si cet arbre contient tous les sommets du graphe, alors le graphe est connexe. Le temps nécessaire pour construire cet arbre est au plus c.n² (où c est une constante et n le nombre de sommets du graphe), donc le problème est dans la classe P.

Aussi, parfois la preuve de l'appartenance à P, qui se fait généralement par la découverte d'un algorithme polynomial, a demandé des années de recherche :

• Le test de primalité AKS est un algorithme qui montre que le problème de savoir si un entier est premier ou non peut être résolu par un algorithme polynomial.

• Programmation linéaire : Les algorithmes de points intérieurs permettent de classer la programmation linéaire dans la classe P. Ce problème est même P-complet.

La classe P peut être définie sur des problèmes algorithmiques généraux pour lesquels il existe une solution en temps polynomial, et pas seulement les problèmes de décision[4], auquel cas ${\displaystyle \mathrm {P} \not \subseteq \mathrm {NP} }$, mais ${\displaystyle \mathrm {P} \cap \mathrm {DEC} \subseteq \mathrm {NP} }$, où DEC est la classe des problèmes de décision.

Représentations des inclusions des classes usuelles.

On a l'inclusion évidente P ${\displaystyle \scriptstyle \subseteq }$ NP, mais l'une des grandes questions ouvertes de l'informatique théorique est le problème P = NP ?.

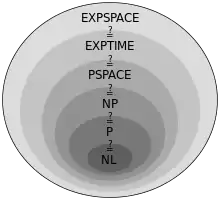
On peut placer P dans la hiérarchie des langages, classés selon l'espace requis : elle contient NL (la classe des problèmes pouvant être résolus sur une machine non-déterministe en espace logarithmique) et est contenu par PSPACE (la classe des problèmes pouvant être résolus en espace polynomial). Les inclusions sont les suivantes (on ne sait pas si elles sont strictes) :

L ⊆ NL ⊆ NC ⊆ P ⊆ NP ⊆ PSPACE ⊆ EXPTIME ⊆ NEXPTIME ⊆ EXPSPACE

P ≠ EXPTIME (d'après le théorème de hiérarchie en temps déterministe)

Par ailleurs, P est le premier niveau de la hiérarchie polynomiale. Et P est incluse dans les classes polynomiales sur des machines plus puissantes (quantiques ou utilisant du hasard par exemple), comme ZPP, BPP et BQP.

Un problème de décision A est dit P-complet, ou complet pour la classe P, s'il est dans la classe P et si tout problème de la classe P peut être réduit à A en espace logarithmique (c'est-à-dire que la traduction d'une instance x du problème à une instance de A peut s'effectuer en utilisant un espace O(log |x|)). Les problèmes suivants sont P-complets.

• Horn-SAT : le problème SAT général est NP-complet, mais sa restriction aux ensembles de clauses de Horn est dans P. Il est P-complet.
• Problème de l'évaluation d'un circuit[5] - [6] : ce problème, en anglais circuit value problem (CVP), consiste à déterminer si, pour un circuit booléen donné, le résultat de la fonction réalisée sur une entrée donnée correspond à une valeur donnée.
• Le problème qui consiste à savoir si le langage dénoté par une grammaire algébrique est vide ou pas[7].
• Décider si le langage d'une grammaire algébrique est infini[8].
• Le problème de vérification de modèles (model checking en anglais) d'une formule de la logique temporelle CTL est dans P[9] - [10] et a été prouvé P-complet [11]. Plus précisément, la démonstration[11] montre que le model checking d'une formule du fragment syntaxique de CTL avec les opérateurs AX (pour tout successeur) et EX (il existe un successeur) est P-difficile. Ainsi, le model checking d'une formule de la logique modale K est P-complet.
• Le problème du flot maximum[12] et donc la programmation linéaire réelle.

S'il existe un langage creux qui est P-complet, alors P = LOGSPACE[13].

On parle dans certains cas, d'algorithmes en temps fortement ou faiblement polynomial. Cette distinction existe pour les problèmes dont l'entrée contient des entiers. On parle de temps faiblement polynomial si les entiers doivent être donnés en écriture unaire (c'est-à-dire que le nombre n compte pour une taille n) pour avoir un temps polynomial, et on parle de temps fortement polynomial si même l'écriture compacte (n a taille log(n)) donne une complexité polynomiale.

Classe NP

P/poly

(en) Sanjeev Arora et Boaz Barak, Computational Complexity : A Modern Approach, Cambridge University Press, 2009 (ISBN 0-521-42426-7), chap. 1 (« The computational model —and why it doesn’t matter »)

(en) La classe P sur le Complexity Zoo