Algorithme de parcours en profondeur

Pour les graphes non orientés, le parcours en profondeur correspond à la méthode intuitive qu'on utilise pour trouver la sortie d'un labyrinthe sans tourner en rond. Des algorithmes de parcours en profondeur sont formulés dès le XIX^e siècle. Édouard Lucas (1891) dans ses Récréations mathématiques en propose une solution rigoureuse[1] dont il attribue l'idée à Charles Pierre Trémaux[2]. Gaston Tarry en donne une autre solution[3].

L'exploration d'un parcours en profondeur depuis un sommet S fonctionne comme suit. Il poursuit alors un chemin dans le graphe jusqu'à un cul-de-sac ou alors jusqu'à atteindre un sommet déjà visité. Il revient alors sur le dernier sommet où on pouvait suivre un autre chemin puis explore un autre chemin (voir vidéo ci-contre). L'exploration s'arrête quand tous les sommets depuis S ont été visités. Bref, l'exploration progresse à partir d'un sommet S en s'appelant récursivement pour chaque sommet voisin de S.

Le nom d'algorithme en profondeur est dû au fait que, contrairement à l'algorithme de parcours en largeur, il explore en fait « à fond » les chemins un par un : pour chaque sommet, il marque le sommet actuel, et il prend le premier sommet voisin jusqu'à ce qu'un sommet n'ait plus de voisins (ou que tous ses voisins soient marqués), et revient alors au sommet père.

Si G n'était pas un arbre, l'algorithme pourrait a priori tourner indéfiniment si on continuait l'exploration depuis un sommet déjà visité. Pour éviter cela, on marque les sommets que l'on visite, de façon à ne pas les explorer à nouveau.

Dans le cas d'un arbre, le parcours en profondeur est utilisé pour caractériser l'arbre.

Durant l'exploration, on marque les sommets afin d'éviter de re-parcourir des sommets parcourus. Initialement, aucun sommet n'est marqué[4].

explorer(graphe G, sommet s)
      marquer le sommet s
      afficher(s)
      pour tout sommet t voisin du sommet s
            si t n'est pas marqué alors
                   explorer(G, t);

Le parcours en profondeur d'un graphe G est alors :

parcoursProfondeur(graphe G)
      pour tout sommet s du graphe G
            si s n'est pas marqué alors
                   explorer(G, s)

On notera qu'il est possible de l'implémenter itérativement à l'aide d'une pile LIFO contenant les sommets à explorer : on désempile un sommet et on empile ses voisins non encore explorés.

Voyons concrètement le fonctionnement du parcours en profondeur depuis le sommet A dans le graphe suivant :

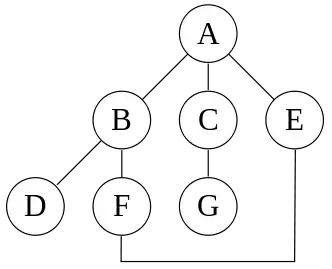
Nous conviendrons que les sommets à gauche sur ce graphe seront choisis avant ceux de droite. Si l'algorithme utilise effectivement un marquage des sommets pour éviter de tourner indéfiniment en boucle, on aura alors l'ordre de visite suivant : A, B, D, F, E, C, G.

Supposons maintenant que nous n'utilisions pas la méthode de marquage, on aurait alors la visite des sommets suivants dans l'ordre: A, B, D, F, E, A, B, D, F, E, etc indéfiniment, puisque l'algorithme ne peut sortir de la boucle A, B, D, F, E et n'atteindra donc jamais C ou G.

Comme les autres algorithmes de parcours de graphe, l'algorithme de parcours en profondeur trouve l'ensemble des sommets accessibles depuis un sommet donné s, c'est-à-dire ceux vers lesquels il existe un chemin partant de s. Il s'agit précisément des sommets marqués par l'algorithme. Ceci s'applique à un graphe orienté ou non orienté. Sur un graphe non orienté, on peut utiliser cette propriété pour le calcul des composantes connexes.

Dans le cas d'un graphe orienté acyclique, le parcours en profondeur permet de calculer un tri topologique des sommets.

L'algorithme de Kosaraju effectue un double parcours en profondeur pour calculer les composantes fortement connexes d'un graphe orienté quelconque.

La complexité du parcours est ${\displaystyle O(|S|+|A|)}$ où ${\displaystyle |S|}$ est le nombre de sommets et ${\displaystyle |A|}$ le nombre d'arcs[4]. En 1985, John Reif a défini un problème de décision associé au parcours en profondeur et a montré qu'il est P-complet[5]. Ce problème décision est le suivant : étant donné un graphe G et deux sommets u et v, décider si u apparait avant v dans le parcours en profondeur qui explore les sommets par ordre lexicographique. Cela signifie que le parcours en profondeur est difficile à paralléliser[6]. Toutefois, le parcours en profondeur (mais pas avec un ordre lexicographique) est parallélisable sur une machine probabiliste et est dans la classe RNC[7]. En 1997, Karger et al. énonce que le problème de savoir si le parcours est parallélisable sur un machine déterministe est ouvert[8].

• Algorithme de parcours en largeur
• Arbre de Galton-Watson
• Arbre enraciné
• Arbre de Trémaux