Arbre de Galton-Watson

Un arbre de Galton-Watson est un arbre (graphe connexe sans cycles) enraciné que l'on note G=(V,E) où V est l'ensemble des nœuds de l'arbre ("vertex" en anglais) et E est l'ensemble des arêtes ("edge" en anglais). Notons ρ ∈ V la racine de l'arbre. Donnons une interprétation des arbres de Galton-Watson avec le vocabulaire d'un arbre généalogique.

• La racine ρ est appelée l'ancêtre commun,
• pour chaque nœud (ou individu) v ∈ V \ {ρ}, le premier nœud sur la trajectoire (unique) de v vers ρ est appelé le père de v.

Notation de Neveu

Figure 1 : Notation de Neveu pour les sommets d'un arbre planaire.

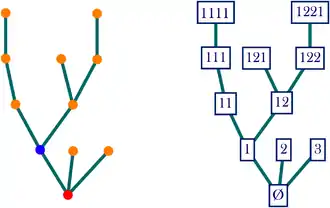
• La racine ρ est notée ${\displaystyle \varnothing }$, l'ensemble vide,
• les fils de ρ sont notés par un entier indiquant leur position dans la fratrie : {1},{2},{3},...
• pour un individu v, noté {v₁,v₂,v₃,...,v_n}, de l'arbre, ses fils seront notés : v1:={v₁,v₂,v₃,...,v_n,1}, v2:={v₁,v₂,v₃,...,v_n,2}, v3:={v₁,v₂,v₃,...,v_n,3},...

Ainsi, un arbre (fini) est défini comme un sous-ensemble ω de l'ensemble des suites finies d'entiers strictement positifs ${\displaystyle U:=\bigcup _{n\geq 0}\mathbb {N} ^{n}}$ (par convention ${\displaystyle \mathbb {N} ^{0}=\varnothing }$) et qui vérifie les trois conditions suivantes :

1. ${\displaystyle \varnothing \in \omega }$,
2. ${\displaystyle \{v_{1},v_{2},\dotsc ,v_{n-1},v_{n}\}\in \omega \Rightarrow \{v_{1},v_{2},...,v_{n-1}\}\in \omega }$,
3. Pour tout ${\displaystyle v\in \omega }$, il existe ${\displaystyle k_{v}(\omega )\in \mathbb {N} }$ avec ${\displaystyle vj\in \omega }$ pour ${\displaystyle 1\leq j\leq k_{v}(\omega )}$.

Dans ce cas ces arbres sont appelés arbres ordonnés et enracinés. Notons ${\displaystyle \mathbb {T} }$ l'ensemble des arbres ordonnés et enracinés.

Pour simplifier la notation, il est courant d'utiliser v₁v₂v₃...v_n pour {v₁,v₂,v₃,...,v_n}. L'entier n est alors appelé la génération de v ou la hauteur de v dans l'arbre, c'est également la distance (de graphe) du nœud à la racine, on le note |v|. La géneration de la racine est 0. L'entier positif k_v(ω) est le nombre d'enfant du nœud v, il est noté k_v s'il n'y a pas d'ambiguïté. Pour un nœud vj de l'arbre, chaque couple (v,vj) est une arête (ou branche de l'arbre). Un nœud f de l'arbre qui n'a pas de fils, c'est-à-dire tel que k_f=0, est une feuille de l'arbre. Les autres nœuds sont appelés nœuds de branchement.

Il est utile de considérer la notion d'arbre "décalé" (shifted tree en anglais). Pour un arbre ${\displaystyle \omega \in \mathbb {T} }$, et pour v un nœud de ω, l'arbre "décalé" ${\displaystyle \theta _{v}\omega$ :=\{vu,u\in U\}} est intuitivement le sous-arbre de ω "au dessus" du nœud v.

L'ensemble U est dénombrable, il peut alors être ordonné en utilisant l'ordre lexicographique par exemple. Ordonnons un arbre fini ω (dont le nombre total de nœuds est un entier |ω| fini) avec l'ordre lexicographique, définissons son parcours de l'arbre en profondeur : on commence par la racine de l'arbre, puis lorsqu'on arrive à un nœud v, on visite son premier fils non encore visité ou on retourne à son père si tous les fils ont été visités, enfin le parcours se termine lorsqu'on revient à la racine et que tous ses fils ont été visités. Par ce parcours, les feuilles sont visitées une fois tandis que les autres nœuds sont visités plusieurs fois. Le nombre total de visites est alors 2|ω|.

Exemple

Dans la figure 1 ci-contre, l'individu 1221 est le premier fils, du deuxième fils, du deuxième fils, du premier fils, de l'ancêtre commun. C'est une feuille de l'arbre de géneration 4. La suite (${\displaystyle \varnothing }$, 1, 11, 111, 1111, 111, 11, 1, 12, 121, 12, 122, 1221, 122, 12, 1, ${\displaystyle \varnothing }$, 2, ${\displaystyle \varnothing }$, 3, ${\displaystyle \varnothing }$) est le parcours en profondeur de l'arbre.

Soit μ=(μ(n),n ≥ 0) une loi de probabilité sur ${\displaystyle \mathbb {N} }$ critique ou sous-critique, c'est-à-dire telle que :

${\displaystyle m:=\sum _{n=0}^{\infty }n\mu (n)\leq 1}$.

On exclut le cas trivial μ(1)=1.

Il existe une unique loi de probabilité ${\displaystyle \mathbb {Q} _{\mu }}$ sur l'ensemble ${\displaystyle \mathbb {T} }$ des arbres ordonnés et enracinés telle que :

1. ${\displaystyle \mathbb {Q} _{\mu }(k_{\varnothing }=j)=\mu (j)}$, pour tout ${\displaystyle j\in \mathbb {N} }$,
2. pour tout ${\displaystyle j\geq 1}$ tel que μ(j) > 0, les arbres « décalés » ${\displaystyle \theta _{1}\omega ,\theta _{2}\omega ,...,\theta _{j}\omega }$ sont indépendants sous la loi conditionnelle ${\displaystyle \mathbb {Q} _{\mu }(\cdot |k_{\varnothing }=j)}$ et leur loi conditionnelle est ${\displaystyle \mathbb {Q} _{\mu }}$.

Un arbre aléatoire de loi ${\displaystyle \mathbb {Q} _{\mu }}$ est appelé un arbre de Galton-Watson avec loi de reproduction μ. (voir §0.2 de Duquesne et Le Gall[2] ou §3 de Neveu[3]).

Intuitivement, la première condition signifie que la loi de reproduction de la racine est μ ; la deuxième condition signifie que les sous-arbres « au-dessus » des fils de la racine sont indépendants les uns des autres et ont tous la même loi qui est celle de l'arbre entier.

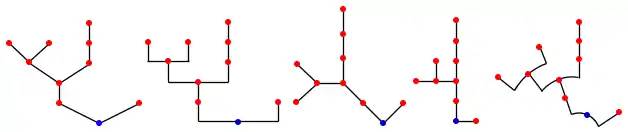
Un arbre est la donnée des nœuds avec leur nombre de fils ordonnés par ordre lexicographique. Il y a donc plusieurs représentations possibles.

• La racine peut se représenter en bas, en haut, à gauche, à droite, au centre (pour un arbre dessiné en cercles),...
• Les nœuds peuvent se représenter par des points ou par des segments (horizontaux, verticaux, ...), ou encore par des arcs de cercle. Tous les nœuds de même génération sont à la même hauteur ou non.
• Les arêtes peuvent se dessiner par des segments tous de même longueur ou non, reliant directement le nœud père et le nœud fils, ou encore reliant le fils et le segment/nœud père, …
• l'angle entre les arêtes peut être variable.

Voici quelques exemples.

Différentes représentations d'un même arbre. Ici les racines sont en bas. Les deux arbres de gauche montrent les générations, les trois de droite ont leurs arêtes de même longueur.

La donnée d'un arbre ω équivaut à la donnée de la suite (k_v(ω),v∈ U). Ainsi, un arbre de Galton-Watson T peut être défini par une suite ${\displaystyle \left(X_{i},i\in U\right)}$ de variables aléatoires iid (indépendantes et identiquement distribuées) à valeurs entières positives.

Il est à remarquer que certaines valeurs de cette suite n'ont pas d'influence sur l'arbre. Le nombre d'éléments efficaces de ${\displaystyle \left(X_{i},i\in U\right)}$ correspond au nombre (aléatoire) total de nœuds dans l'arbre de Galton-Watson.

Exemple

La suite finie, donnée par ordre lexicographique, (k_{${\displaystyle \emptyset }$}, k₁, k₁₁,k₁₁₁,k₁₁₁₁,k₁₂,k₁₂₁,k₁₂₂,k₁₂₂₁,k₂,k₃)= (3,2,1,1,0,2,0,1,0,0,0) caractérise l'arbre de la figure 1. La valeur de k₄ ne joue pas de rôle ici puisque la racine n'a pas de quatrième fils.

Marche de Łukasiewicz

Figure 2 : Arbre fini et sa marche de Łukasiewicz associée.

Pour un arbre fini ω, la marche de Łukasiewicz est définie par :

${\displaystyle V:\{0,...,|\omega |\}\rightarrow \mathbb {N} }$

${\displaystyle \displaystyle V(0)=0}$

${\displaystyle V(k)-V(k-1)=k_{v_{k}}(\omega )-1}$

où ${\displaystyle v_{k}}$ est le k-ième individu de l'arbre par ordre lexicographique. La suite V caractérise l'arbre ω, puisqu'elle est équivalente à la donnée de la suite ${\displaystyle (k_{v_{k}}(\omega ),1\leq k\leq |\omega |)}$.

Propriétés

• pour tout 0 ≤ k ≤ |ω|-1, V(k) ≥ 0,
• V(|ω|)= -1,
• ses accroissements ${\displaystyle V(k)-V(k-1)}$ sont à valeurs dans {-1, 0, 1,...},

Figure 3 : Construction de l'arbre (en bleu avec nœuds en rouge) à partir d'une marche de Łukasiewicz.

Proposition (voir §0.2 de Duquesne et Le Gall[2])

Si T est un arbre de Galton-Watson de loi de reproduction donnée par ${\displaystyle (p_{n},n\geq 0)}$ où ${\displaystyle p_{n}}$ est la probabilité d'avoir n fils, alors V est une marche aléatoire dont la loi des sauts est donnée par ${\displaystyle \mathbb {P} (V(k)-V(k-1)=n)=p_{n+1}}$ et stoppée lorsqu'elle atteint -1.

Remarque

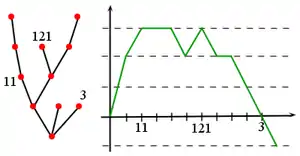
Soit k un entier fixé. Si un entier n ≤ k-1 vérifie la condition ${\displaystyle V(n)=\inf _{j\in [n,k]}V(j)}$, alors l'individu dénommé n est un ancêtre de l'individu k. On peut ainsi reconstituer l'arbre à partir de la trajectoire de la marche de Łukasiewicz en reliant les points (n,V(n)) du graphe de V avec ses infima précédents (voir Figure 3 ci-contre).

Processus de contour

Figure 4 : Arbre fini et son processus de contour associé. en bleu: parcours en profondeur.

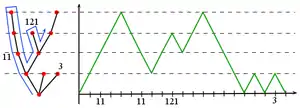
Pour un arbre fini ω, le processus de contour (ou fonction de contour ou marche de Harris ou chemin de Dyck) est défini par :

${\displaystyle C:\{0,...,2|\omega |-1\}\rightarrow \mathbb {N} }$

${\displaystyle k}$ ${\displaystyle \mapsto |v_{k}|}$

qui, à chaque étape k du parcours en profondeur, associe la génération de l'individu v_k visité. Le processus de contour est parfois défini comme l'interpolation linéaire de la fonction C, on garde alors la même notation.

Le nom contour est issu du parcours en profondeur qui "contourne l'arbre par la gauche".

Figure 5 : Construction de l'arbre (en bleu avec les nœuds en rouge) à partir d'un processus de contour.

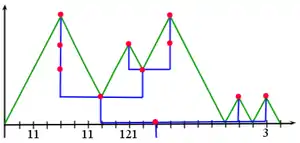
Propriétés

• La fonction C est positive,
• elle s'annule en 0 et en 2|ω|-1,
• pour tout 1 ≤ k ≤ 2|ω|-1, ${\displaystyle |C(k)-C(k-1)|=1}$,
• il existe une bijection entre les arbres de taille n et les fonctions ${\displaystyle C:[0,2n-1]\rightarrow \mathbb {N} }$ (voir §6.3 de Pitman[4]).

Proposition (voir §6.3 de Pitman[4])

Si T est un arbre de Galton-Watson conditionné à avoir n nœuds et dont la loi de reproduction est une loi géométrique, alors son processus de contour est l'excursion d'une marche aléatoire simple conditionnée à avoir une longueur 2n.

Si T est un arbre de Galton-Watson conditionné à avoir n nœuds avec une loi de reproduction quelconque, alors son processus de contour n'est plus l'excursion d'un processus aléatoire markovien.

Remarque

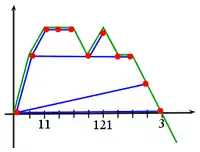
Le processus de contour prend la même valeur aux différents passages du parcours en profondeur en un même nœud de l'arbre. On peut ainsi représenter un nœud de l'arbre par un segment horizontal sous le graphe du processus de contour. Les excursions du graphe "au-dessus" de ce segment correspondent aux sous-arbres "au-dessus" de ce nœud. On peut ainsi reconstituer l'arbre à partir du processus de contour (voir Figure 5 ci-contre).

Processus des hauteurs

Figure 6 : Arbre fini et son processus des hauteurs associé.

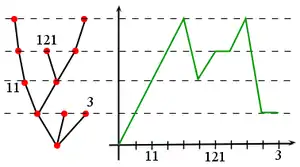
Pour un arbre fini ω, le processus des hauteurs (ou fonction des hauteurs) est défini par :

${\displaystyle H:\{0,...,|\omega |-1\}\rightarrow \mathbb {N} }$

${\displaystyle k}$ ${\displaystyle \mapsto |v_{k}|}$

tel que H(k) soit la génération du k-ième individu de l'arbre par ordre lexicographique.

Intuitivement, le processus des hauteurs est similaire au processus de contour mais chaque individu de l'arbre n'est visité qu'une fois.

Propriétés

• La fonction H sont strictement positive pour tout 1 ≤ k ≤ |ω|-1,
• elle s'annule en 0,
• ses accroissements ${\displaystyle H(k)-H(k-1)}$ sont à valeurs dans {..., -2, -1, 0, 1},
• le processus des hauteurs caractérise l'arbre ω.

Proposition (voir §0.2 de Duquesne et Le Gall[2])

Soit T est un arbre de Galton-Watson de loi de reproduction donnée par ${\displaystyle (p_{n},n\geq 0)}$ où ${\displaystyle p_{n}}$ est la probabilité d'avoir n fils et H son processus des hauteurs associé. Alors ce dernier n'est pas un processus aléatoire markovien mais il peut s'écrit en fonction de la marche de Łukasiewicz V associée à T par la formule :

${\displaystyle H(k)=Card\{n\in \{0,1,...,k-1\}:V_{n}=\inf _{n\leq j\leq k}V_{j}\}.}$

Proposition

On peut retrouver le processus de contour à partir du processus des hauteurs. Notons K(n)= 2n-H(n). On retrouve le processus de contour par la formule (donnée ici pour l'interpolation linéaire) :

${\displaystyle C(t)=\left(H(n)-t+K(n)\right)^{+}}$ si ${\displaystyle t\in [K(n),K(n+1)-1[}$

${\displaystyle =\left(t-K(n+1)+H(n+1)\right)^{+}}$ si ${\displaystyle t\in [K(n+1)-1,K(n+1)[}$

Considérons un arbre de Galton-Watson T de loi de reproduction μ. Considérons Z_n(T) le nombre d'individus à la n-ième génération, potentiellement nul :

${\displaystyle Z_{n}(T):=Card\{v\in T\,\,;\,|v|=n\}.}$

Proposition (voir §3 de Neveu[3])

La suite (Z_n(T),n ≥ 1) de variables aléatoires est un processus de Galton-Watson de loi de reproduction μ et partant de Z₀(T)=1.

Remarques

• Le temps du processus de Galton-Watson correspond à la génération de l'arbre associé,
• La probabilité d'extinction d'un processus de Galton-Watson (probabilité qu'en un temps fini N on ait Z_N(T)=0) correspond à la probabilité que l'arbre associé soit fini (qu'il contienne un nombre fini d'individus, c'est-à-dire un nombre fini de générations).

Théorème

En fonction de la moyenne m associée à la loi de reproduction μ, on distingue trois cas :

• Cas souscritique (m<1). La probabilité que l'arbre de Galton-Watson soit fini vaut 1.
• Cas critique (m =1). La probabilité que l'arbre de Galton-Watson soit fini vaut 1 (on rappelle que μ(1)≠1)
• Cas surcritique (m>1). La probabilité que l'arbre de Galton-Watson soit fini est strictement inférieure à 1.

Une forêt de Galton-Watson de loi de reproduction μ est une suite (finie ou infinie) d'arbres de Galton-Watson indépendants de même loi de reproduction μ. La loi d'une forêt de Galton-Watson est une loi de probabilité sur l'espace ${\displaystyle \mathbb {T} ^{\mathbb {N} }}$.

Considérons une forêt de Galton-Watson ${\displaystyle {\mathcal {F}}={\mathcal {F}}((T_{k})_{k\geq 1})}$. Notons ${\displaystyle (V_{n}(T_{k}),0\leq n\leq |T_{k}|)}$, ${\displaystyle (C_{n}(T_{k}),0\leq n\leq 2|T_{k}|-1)}$ et ${\displaystyle (H_{n}(T_{k}),0\leq n\leq |T_{k}|-1)}$ la marche de Łukasiewicz, le processus de contour et le processus des hauteurs de l'arbre T_k. On pose également H_|Tk|(T_k)=0. La marche de Łukasiewicz ${\displaystyle (V_{n}({\mathcal {F}}),n\geq 0)}$, le processus de contour ${\displaystyle (C_{n}({\mathcal {F}}),n\geq 0)}$, et le processus des hauteurs ${\displaystyle (H_{n}({\mathcal {F}}),n\geq 0)}$ de ${\displaystyle {\mathcal {F}}}$ sont les concaténations respectives des marches de Łukasiewicz, des processus de contour et des processus des hauteurs des arbres de la forêt :

${\displaystyle V({\mathcal {F}}):n\mapsto V_{n}({\mathcal {F}}):=V_{n-|T_{1}|-...-|T_{k-1}|}(T_{k})-k+1}$ si ${\displaystyle |T_{1}|+...+|T_{k-1}|\leq n\leq |T_{1}|+...+|T_{k}|}$ ,

${\displaystyle C({\mathcal {F}}):n\mapsto C_{n}({\mathcal {F}}):=C_{n-2|T_{1}|-...-2|T_{k-1}|}(T_{k})}$ si ${\displaystyle 2|T_{1}|+...+2|T_{k-1}|\leq n\leq 2|T_{1}|+...+2|T_{k}|}$ ,

${\displaystyle H({\mathcal {F}}):n\mapsto H_{n}({\mathcal {F}}):=H_{n-|T_{1}|-...-|T_{k-1}|}(T_{k})}$ si ${\displaystyle |T_{1}|+...+|T_{k-1}|\leq n\leq |T_{1}|+...+|T_{k}|-1}$.

Si la forêt est une suite finie d'arbres, ces trois processus restent constants après la dernière valeur issue de la définition précédente.

Notons ${\displaystyle {\mathcal {F}}^{k,n}}$ une forêt de k arbres et conditionnées à avoir n nœuds, c'est-à-dire une forêt (T₁,...,T_k) sous la loi conditionnelle ${\displaystyle \mathbb {Q} _{\mu }(\cdot ||T_{1}|+...+|T_{k}|=m)}$. Les forêts conditionnelles sont caractérisées par les trois précédents processus.

Proposition

Soit ${\displaystyle {\mathcal {F}}}$ une forêt de Galton-Watson de loi ${\displaystyle \mathbb {Q} _{\mu }}$. Sous la loi ${\displaystyle \mathbb {Q} _{\mu }(\cdot ||T_{1}|+...+|T_{k}|=m)}$ la marche de Łukasievwicz ${\displaystyle (V_{n},0\leq n\leq m)}$ jusqu'au temps m, a même loi que la marche de Łukasievwicz stoppée lorsqu'elle atteint le niveau -k.

Considérons une suite ${\displaystyle (Z^{p},p\geq 1)}$ de processus de Galton-Watson telle que chaque processus de Galton-Watson ${\displaystyle (Z_{n}^{p},n\in \mathbb {N} )}$ ait pour loi de reproduction ${\displaystyle \mu _{p}}$ (critique ou sous-critique) et ${\displaystyle Z_{0}^{p}=p}$. C'est-à-dire qu'il y a initialement p individus.

Notons ${\displaystyle (V^{p},p\geq 1)}$, ${\displaystyle (C^{p},p\geq 1)}$ et ${\displaystyle (H^{p},p\geq 1)}$ les suites des marches de Łukasiewicz, des processus de contour et des processus des hauteurs des forêts associées à ${\displaystyle (Z^{p},p\geq 1)}$.

Le théorème suivant donne un résultat de convergence type Donsker pour ces processus discrets vers des processus continus.

Théorème (citons Grimvall en 1974, Duquesne et Le Gall en 2002[2])

Sous une hypothèse technique donnée dans la remarque en fin de Théorème, il existe une suite croissante ${\displaystyle (\gamma _{p},p\geq 1)}$ d'entiers naturels convergente vers ${\displaystyle +\infty }$ telle que :

${\displaystyle \left({\frac {1}{p}}Z_{[\gamma _{p}t]}^{p}\right)_{t\geq 0}{\underset {p\rightarrow \infty }{\Longrightarrow }}\left(Y_{t}\right)_{t\geq 0}}$ et

${\displaystyle \left({\frac {1}{p}}V_{[p\gamma _{p}t]}^{p},{\frac {1}{\gamma _{p}}}C_{[2p\gamma _{p}t]}^{p},{\frac {1}{\gamma _{p}}}H_{[p\gamma _{p}t]}^{p}\right)_{t\geq 0}{\underset {p\rightarrow \infty }{\Longrightarrow }}\left(X_{t},H_{t},H_{t}\right)_{t\geq 0}}$

où [.] est la partie entière et la convergence ${\displaystyle \Longrightarrow }$ est une convergence en loi des processus stochastiques dans l'espace de Skorokhod.

• le processus ${\displaystyle Y=(Y_{t},t\geq 0)}$ est un processus stochastique à temps continu et à valeurs continues appelé processus de branchement à espace d'état continu (CSBP) de mécanisme de branchement ψ. C'est l'analogue continu d'un processus de Galton-Watson.
• Le processus ${\displaystyle X=(X_{t},t\geq 0)}$ est un processus de Lévy (à temps continu et à valeurs continues) sans sauts négatifs et qui ne tend pas vers ${\displaystyle +\infty }$. Son exposant de Laplace est ψ.
• Le processus ${\displaystyle H=(H_{t},t\geq 0)}$ est un processus stochastique à temps continus et à valeurs continues appelé le processus des hauteurs (continu) associé à X et à Y.

Intuitivement, il existe des renormalisations en espace et en temps telles que les quatre suites de processus discrets codant des forêts discrètes convergent (en loi) vers des processus continus lorsque le nombre de racines des forêts tend vers ${\displaystyle +\infty }$.

Remarques

• hypothèse technique : le Théorème précédent est vrai sous les deux conditions suivantes :

${\displaystyle \int _{1}^{\infty }{\frac {du}{\psi (u)}}<\infty }$ et ${\displaystyle \forall \delta >0,\,\,\,\,{\underset {p\rightarrow \infty }{\lim }}\inf \mathbb {P} [Z_{[\delta \gamma _{p}]}^{p}=0]>0}$ .

• On peut construire un arbre continu (analogue des arbres discrets) en utilisant les méthodes précédentes pour les arbres de Galton-Watson. L'arbre obtenu est appelé arbre réel.

Cas particulier

Dans le cas où les lois de reproduction ${\displaystyle \mu _{p}}$ sont à variance finie, Le processus X est un mouvement brownien standard et le processus H est un mouvement brownien réfléchi en 0. L'arbre associé est appelé arbre brownien.