Marche aléatoire
En mathématiques, en économie et en physique théorique, une marche aléatoire est un modèle mathématique d'un système possédant une dynamique discrète composée d'une succession de pas aléatoires, ou effectués « au hasard ». On emploie également fréquemment les expressions marche au hasard, promenade aléatoire ou random walk en anglais. Ces pas aléatoires sont de plus totalement décorrélés les uns des autres ; cette dernière propriété, fondamentale, est appelée caractère markovien du processus, du nom du mathématicien Markov. Elle signifie intuitivement qu'à chaque instant, le futur du système dépend de son état présent, mais pas de son passé, même le plus proche. Autrement dit, le système « perd la mémoire » à mesure qu'il évolue dans le temps. Pour cette raison, une marche aléatoire est parfois aussi appelée « marche de l'ivrogne ».
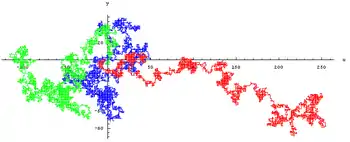
Cette modélisation mathématique permet de rendre compte de certains phénomènes naturels, dont l'exemple le plus fameux est le mouvement brownien, correspondant par exemple aux mouvements en apparence aléatoires des particules présentes dans le fluide intérieur d'un grain de pollen.
En mathématiques ou en informatique, on étudie souvent des marches au hasard sur des réseaux réguliers ou sur des graphes plus complexes. C'est par exemple la méthode utilisée par le moteur de recherche Google pour parcourir, identifier et classer les pages du réseau internet.
Techniquement, les marches aléatoires sont du domaine de la théorie des probabilités. Une marche aléatoire est en effet un processus stochastique du type chaîne de Markov. Elle se décompose en unités élémentaires appelées pas, dont la longueur peut être elle-même constante, aléatoire ou fixée par le réseau ou le graphe sur lequel on circule. À chaque pas, on a donc un éventail de possibilités pour sélectionner au hasard la direction et la grandeur du pas. Cet éventail de possibilités peut être discret (choix parmi un nombre fini de valeurs), ou continu.
Historique
L'idée de marche aléatoire a été introduite (sans le nom) en 1905 par le biostatisticien Karl Pearson pour rendre compte des migrations d'une population de moustiques dans une forêt. Pearson y pose la question suivante[1] :
« Un homme part d'un point O et parcourt l yards (0,914 m) en ligne droite ; il tourne d'un angle quelconque, et marche de nouveau l yards en ligne droite. Il répète ce processus n fois. Je demande la probabilité qu'après n de ces trajets, il soit à une distance située entre r et r + dr de son point de départ. »
La réponse à cette question est fournie une semaine plus tard par Lord Rayleigh dans la livraison suivante de la revue Nature : lorsque n est suffisamment grand, cette probabilité vaut :
Si Rayleigh fournit si rapidement la réponse[2], c'est qu'il a lui-même étudié en 1880 un problème connexe : le comportement d'une superposition d'ondes acoustiques toutes de même amplitude, mais de phases aléatoires. Pearson répond à Rayleigh le [3] :
« J'aurais dû le savoir, mais mes lectures ces dernières années se sont déplacées vers d'autres centres d'intérêt, et on ne s'attend pas à trouver la première étape d'un problème de biométrie dans un mémoire sur l'acoustique. »
Pearson poursuit ensuite :
« La leçon de la solution de Lord Rayleigh est que, dans un pays ouvert, l'endroit le plus probable pour trouver un ivrogne encore capable de tenir sur ses pieds se trouve quelque part dans le voisinage de son point de départ. »
L'expression « marche aléatoire » n'a été introduite que vers 1919-1921 par le mathématicien hongrois George Pólya, qui utilisait le mot allemand « Irrfahrt ».
Marche aléatoire discrète à une dimension
Définition
Le modèle de marche aléatoire le plus simple est celui de la marche aléatoire discrète à une dimension sur le réseau périodique ℤ. Pour en former un exemple concret, on peut imaginer un individu (ou « particule ») sur un escalier, qui tire à pile ou face pour décider si le prochain pas sera vers le haut ou vers le bas. À chaque étape, il n'y a que deux possibilités : sur cet exemple, un pas en avant ou un pas en arrière. Le seul paramètre libre du problème est la probabilité que la particule fasse un saut en avant (plutôt qu'un saut en arrière).
Si on nomme cette probabilité par le nombre réel p tel que : 0 < p < 1, alors q = 1 – p représente la probabilité que la particule fasse un saut en arrière.
Le cas le plus simple, qui correspond par exemple au mouvement brownien, consiste à faire l'hypothèse d'isotropie spatiale. Les directions « avant / arrière » de l'espace physique étant a priori équivalentes, on pose l'équiprobabilité :
Il est remarquable que les lois mises en évidence dans ce cas s'étendent à des problèmes de marches aléatoires beaucoup plus complexes.
Marche aléatoire isotrope
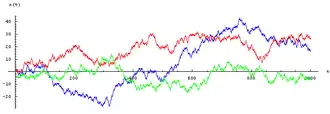
Chacun des tirs au hasard pour choisir le mouvement constitue une épreuve de Bernoulli avec issues équiprobables : ici la probabilité de montée ou de descente est 1/2.
La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les positions successives x(t) de la particule aux instants t = 1, 2,..., partant de la condition initiale x(0)=0.
Après n pas au total, le nombre de fois où on a tiré « pile » suit la loi binomiale B(n,1/2), de sorte que la probabilité vaut :
où est le nombre de combinaisons de k éléments pris parmi n.
On peut déterminer la position après n itérations, en prenant la valeur 0 pour le départ, en ajoutant 1 pour chaque pas en avant (pile), en retranchant 1 pour chaque pas en arrière (face). Alors la position est donnée par : . Par rapport à la loi binomiale classique, il suffit donc de décaler les résultats de n⁄2 et de multiplier par 2, ainsi :
- si n et k ont même parité, = 0 sinon ;
- l'espérance est nulle ;
- la variance vaut n et l'écart type √n ;
- on a toujours l'inégalité de Bienaymé-Tchebychev ;
- et la loi des grands nombres.
Concrètement, si on renouvelle l'expérience avec un grand nombre de participants, et si on les laisse évoluer pendant un nombre de pas assez important (de l'ordre de n = 100 par exemple) on s'attend à ce que le nuage des positions finales soit en gros centré sur la marche initiale. Ceci peut être rendu quantitatif : en se plaçant dans le régime asymptotique n >> 1, on démontre en utilisant la formule de Stirling que la loi binomiale se comporte asymptotiquement comme une distribution gaussienne. On obtient notamment un ordre de grandeur de l'étalement du nuage de participants : par exemple on s'attend à ce que 95 % environ des participants soient restés à 20 pas ou moins de la position initiale (20=2√100).
Exemples
La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le réseau ℤ après 1 000 pas, partant de l'origine. Les lignes en pointillés indiquent respectivement les valeurs maximum et minimum de la position atteintes (après 1 000 pas).
Problème du retour à l'origine
D'après la formule ci-dessus, la probabilité de revenir à l'origine au bout de 2n pas vaut (elle est bien sûr nulle après un nombre impair de pas).
L'équivalent obtenu par la formule de Stirling montre que cette probabilité tend lentement vers 0 ce qui signifie intuitivement que plus le temps passe, moins on a de chance de se trouver au point de départ. Cependant nous allons voir que toute marche revient au moins une fois à l'origine, tout en sachant que la moyenne des temps de premier retour à l'origine est infinie.
Probabilité de passage à l'origine
On se demande quelle est la probabilité d'être revenu au moins une fois à l'origine lors d'un parcours de longueur 2n ; il est remarquable que l'évènement contraire a aussi pour probabilité et que donc tend vers 1 lorsque n tend vers l'infini : une marche aléatoire isotrope sur la droite repasse presque surement au moins une fois à son point de départ (donc en fait y repasse une infinité de fois), et ceci vaut même pour tout point par lequel elle passe. On verra plus loin que ceci reste vrai en dimension 2, mais devient faux en dimension supérieure.
Démonstration de la formule précédente :
Pour raison de symétrie, le nombre de marches aléatoires de longueur ne repassant pas par est le double du nombre de celles qui restent .
Notre problème est de dénombrer les marches allant de à en coups et se situant, à part , strictement à droite de .
Le premier segment d'une telle marche allant forcément de à , il suffit de compter le nombre de chemins qui vont de à en coups sans passer par .
D'une façon générale, le nombre de chemins qui vont de à en coups vaut (le chemin est entièrement déterminé par les déplacements vers la droite (ou les déplacements vers la gauche)), à choisir parmi les déplacements totaux. Donc déjà, le nombre total de marches qui vont de à vaut
La partie délicate est de déterminer le nombre de marches de à en coups qui passent par 0. On utilise pour cela le principe de réflexion, (voir l'article sur le problème du scrutin).
Pour une telle marche, on peut remplacer bijectivement la partie entre le de départ et le premier retour en par son symétrique par rapport à : ce nombre est donc le même que celui des marches allant de à en coups soit
.Le nombre de marches allant de à de longueur sans passer par l'axe vaut donc . Notons que ce résultat est équivalent à celui du théorème du scrutin.
On en déduit le nombre de marches évitant : ; somme télescopique donnant , ce qu'il fallait démontrer.
Autre interprétation du même résultat : le nombre de mots binaires de longueur dont tous les sous-mots commençant par la gauche (resp. par la droite) présentent strictement plus de 1 que de 0 (resp. l'inverse) vaut (ne pas confondre avec les mots de Dyck).
Un calcul similaire montre que dans le cas impair, la probabilité de retour à l'origine lors d'un parcours de longueur vaut aussi (voir la suite A063886 de l'OEIS et la suite A307768 de l'OEIS).
Temps de premier retour à l'origine
En utilisant des résultats précédents, on peut obtenir la probabilité que la marche revienne à l'origine pour la première fois au temps : . On en déduit que l'espérance du temps de premier retour à l'origine est infinie puisque .
Démonstration de la formule précédente :
Une marche qui revient à l'origine au temps passe forcément par 1 ou par -1 au temps précédent et, toujours par symétrie, il y a autant de marches arrivant en 1 qu'en -1 ; le nombre de marches revenant à l'origine pour la première fois au temps vaut donc le double du nombre de marches de longueur aboutissant en 1 et restant >0 ; on peut refaire un raisonnement du type précédent ou appliquer directement la formule du scrutin avec , d'où , ce que nous voulions.
Notons que est le double du nombre de Catalan d'ordre .
Marche aléatoire isotrope sur un réseau à x dimensions
Deux dimensions
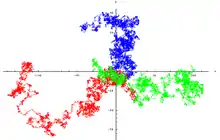
On considère une marche aléatoire sur le réseau plan ℤ2. Il y a ici quatre mouvements possibles à chaque site : en avant, en arrière, à droite, à gauche. La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les trois trajectoires obtenues.
Pour des longues marches, la distribution de la position finale du marcheur se comporte asymptotiquement comme une distribution gaussienne. Cette convergence est illustrée ci-dessous : on trace les répartitions des probabilités de présence sur le réseau après 10 pas, puis après 60 pas :


Spécimens
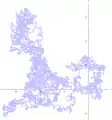
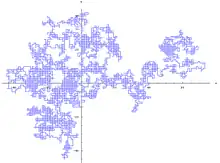
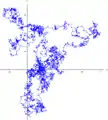
La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le réseau ℤ2 après 10 000 pas, partant de l'origine.
Trois dimensions
On considère une marche aléatoire sur le réseau cubique ℤ3. Il y a ici six mouvements possibles à chaque site : en avant, en arrière, à droite, à gauche, en haut, en bas.

La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les trois trajectoires obtenues.
Spécimens
La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le réseau ℤ3 après 10 000 pas, partant de l'origine.
Projections bidimensionnelles
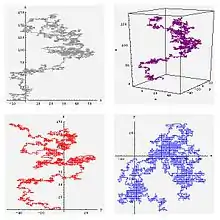
Marche aléatoire isotrope sur un continuum à x dimensions
Deux dimensions
On considère la marche aléatoire sur le plan ℝ2 définie par le processus suivant :

- la particule est initialement à l'origine : x(0) = 0, y(0) = 0 et se déplace sur le plan par des sauts successifs effectués toutes les secondes.
- à chaque saut, la particule avance d'une longueur unité dans une direction caractérisée par un angle polaire α défini par rapport à l'axe (Ox). On choisit par exemple : –π ≤ α < +π.
- Cet angle polaire α est une variable aléatoire, caractérisée par une densité de probabilité f (α). Le processus est isotrope lorsque toutes les directions sont équiprobables, ce qui correspond au choix d'une densité uniforme :
Chaque direction de saut est totalement indépendante de la direction du saut précédent.
La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les trois trajectoires obtenues.
Spécimens
La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le plan ℝ2 après 10 000 pas, partant de l'origine.
Récurrence et dimension de l'espace
Récurrence
Considérons une marche aléatoire isotrope sur le réseau ℤd à d dimensions spatiales. On peut toujours choisir de prendre le point de départ de cette marche comme origine O du système de coordonnées cartésiennes. La question de la récurrence consiste alors à se demander si on peut trouver au moins un[4] instant t positif fini pour lequel la particule repasse par l'origine O.
La marche aléatoire sera dite récurrente si et seulement si la probabilité que la particule repasse à l'origine O pour un certain instant t ultérieur fini vaut un.
Théorème de Pólya (1921)
Cette propriété de récurrence dépend fortement de la dimension de l'espace ; on peut en effet démontrer que[5] - [6] - [7] - [8] - [9] (Pólya - 1921)[10] :
- pour d = 1 et d = 2, la marche aléatoire isotrope est récurrente.
- pour d = 3 et au-delà, la marche aléatoire isotrope n'est pas récurrente ; on dit alors qu'elle est transitoire (en bon « franglais », certains auteurs utilisent parfois le mot anglais transient).
Certains disent parfois en plaisantant que ce théorème est au fondement du proverbe : « Tous les chemins mènent à Rome ». Le lecteur notera que si l'on inclut les chemins « cosmiques », alors le proverbe est faux[6].
Probabilité de retour à l'origine en dimension supérieure ou égale à trois
On sait en fait calculer la probabilité que le marcheur, parti initialement de l'origine, revienne à l'origine, et ce pour toutes les dimensions d > 2. Cette probabilité p(d) admet l'expression suivante[11] :
où u(d) est une intégrale à d dimensions :
- , pouvant s'exprimer à l'aide de la fonction de Bessel de première espèce :
- .
Le nombre représente le nombre moyen de retours à l'origine avant d'aller à l'infini (voir à loi géométrique).
Le cas particulier d = 3 avait en fait déjà été obtenu précédemment par Watson[12], Mc Crea et Whipple[13], et Domb[14]. Une expression analytique de l'intégrale n'a été obtenue qu'en 1977 par Glasser et Zucker[15] - [16] :
où Γ est la fonction gamma. Les expressions analytiques de u(d) ne sont pas connues en dimension d supérieure ou égale à 4[16].
On obtient les valeurs numériques suivantes[17] :
- , suite A086231 de l'OEIS, , suite A086230 de l'OEIS ;
- , suite A242812 de l'OEIS, , suite A086232 de l'OEIS ;
- , suite A242813 de l'OEIS, , suite A086233 de l'OEIS ;
- , suite A242814 de l'OEIS, , suite A086234 de l'OEIS ;
- , suite A242815 de l'OEIS, , suite A086235 de l'OEIS ;
- , suite A242816 de l'OEIS, , suite A086236 de l'OEIS .
Marche aléatoire sur un groupe
On considère un groupe supposé ici multiplicatif, sans que ce soit essentiel à la définition d'une marche aléatoire sur un groupe. On se donne une suite de variables aléatoires indépendantes et de même loi (loi qu'on appelle ici par exemple), variables aléatoires toutes à valeurs dans . On se donne aussi une variable aléatoire à valeurs dans , de loi quelconque, et indépendante de . On pose alors, pour
La suite est alors une chaîne de Markov, et est dite marche aléatoire sur G, de pas . Ce qualificatif s'applique aussi à toute suite aléatoire de même loi que X. Alternativement, on accepte comme marche aléatoire une suite définie par la relation de récurrence :
Pour distinguer les deux types de chaines de Markov ainsi définies, on parle parfois de marche aléatoire droite et de marche aléatoire gauche. Le terme général de la matrice de transition de cette chaine de Markov est défini, pour , par
suivant que la marche aléatoire est droite ou gauche. On vérifie sans peine que
car et sont des bijections de G dans G. Ainsi, une mesure uniforme sur est une mesure stationnaire.
les marches aléatoires mentionnées plus haut sont des marches aléatoires sur les groupes additifs ℤd et ℝ2.
Marche aléatoire sur un graphe
En informatique, la marche aléatoire sur un graphe est utilisée notamment dans l'algorithme de Wilson afin de récupérer un arbre couvrant aléatoire.
Un algorithme de marche aléatoire consiste à partir d'un sommet u donné et à chaque étape choisir un voisin v de u et répéter ce processus avec v.
Dans l'algorithme de Wilson, on utilisera un type de marche aléatoire qui s'appelle la "Marche aléatoire à boucles effacées" (Random erased loops walk) où comme son nom l'indique, on retirera les cycles du chemin obtenu à la fin de la marche.
Marche aléatoire continue
Très utilisée dans la modélisation de séries temporelles continues, une marche aléatoire peut s'écrire :
Il s'agit d'un cas particulier d'un processus autorégressif (c'est-à-dire « régressé sur lui-même ») avec ρ = 1. La valeur du paramètre ρ est très importante car elle change fondamentalement la propriété de la série :
De manière récursive, une marche aléatoire est simplement la somme de bruits blancs. On l'écrit :
Notes et références
- Karl Pearson, Nature, 27 juillet 1905, DOI 10.1038/072294b0.
- Cette densité de probabilité est depuis lors appelée loi de Rayleigh.
- Karl Pearson, Nature, 10 août 1905.
- S'il en existe un, il en existera en général une infinité. Le plus petit de tous ces instants finis est appelé instant de premier retour à l'origine. Cf. par ex. Stroock 2005, chap. 1.
- Cf. par ex. Stroock 2005, chap. 1.
- (en) Yakov G. Sinai, Probability Theory - An Introductory Course, Springer-Verlag, (lire en ligne), p. 71.
- (en) Jonathan Novak, « Pólya's random walk theorem », American Mathematical Monthly, vol. 121, no 8, , p. 711-716 (arXiv 1301.3916).
- Olivier Garet et Aline Kurtzmann, De l'intégration aux probabilités, Ellipses, , 2e éd. (lire en ligne), p. 259-260.
- Michel Benaïm et Nicole El Karoui, Promenade aléatoire : chaînes de Markov et simulations, martingales et stratégies, Éditions École Polytechnique, (lire en ligne), p. 83-85.
- (de) Georg Pólya, « Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Straßennetz », Mathematische Annalen, vol. 83, 1921, p. 149-160.
- (en) E. W. Montroll, « Random walks in multidimensional spaces, especially on periodic lattices », Journal of the SIAM, vol. 4, , p. 241-260.
- (en) G. N. Watson, « Three triple integrals », Quarterly Journal of Mathematics, vol. 2, no 10, , p. 266-276.
- (en) W. H. McCrea et F. J. W. Whipple, « Random paths in two and three dimensions », Proceedings of the Royal Society of Edinburgh, vol. 60, , p. 281-298.
- (en) C. Domb, « On multiple returns in the random-walk problem », Proceedings of the Cambridge Philosophical Society, vol. 50, , p. 586-591.
- (en) M. L. Glasser et I. J. Zucker, « Extended Watson integrals for the cubic lattices », PNAS, vol. 74, , p. 1800-1801.
- (en) Eric W. Weisstein, « Pólya's Random Walk Constants », sur MathWorld.
- (en) Steven R. Finch, Mathematical Constants, Cambridge University Press, , 602 p. (ISBN 978-0-521-81805-6, lire en ligne), p. 322.
Voir aussi
Ouvrages de références
- (en) Joseph Rudnick et George Gaspari, Elements of the Random Walk : An introduction for Advanced Students and Researchers, Cambridge University Press, , 346 p. (ISBN 0-521-82891-0)
- (en) Frank Spitzer, Principles of the Random Walk, Princeton University Press, (lire en ligne)Réédité par Springer (1970) (ISBN 0-387-90139-6) ; 2e édition dans la collection Graduate Texts in Mathematics 34 (2001) (ISBN 0-387-95154-7)
- (en) Daniel W. Stroock, An Introduction to Markov Processes, Springer, coll. « Graduate Texts in Mathematics », , 178 p. (ISBN 978-3-540-23451-7, lire en ligne)
- (en) William Feller, An Introduction to Probability Theory and Its Applications, volume 1, John Wiley & Sons, coll. « Wiley Series in Probability and Statistics », , 528 p. (ISBN 978-0-471-25708-0)
Articles classiques
- (en) Mark Kac, Random Walk and the Theory of Brownian Motion, American Mathematical Monthly 54(7) (1947), 369-391. (en) Texte au format [PDF] Cet article est l'un des six contenus dans : Selected Papers on Noise & Stochastic Processes, Charles Proteus Steinmetz & Nelson Wax (eds.), Dover, 1954. Réédité dans la collection Phoenix (2003), ASIN 0486495353.
- (en) Subramaniam Chandrashekhar, Stochastic Problems in Physics & Astronomy, Review of Modern Physics 15 (1943), 1-89. Cet article est l'un des six contenus dans : Selected Papers on Noise & Stochastic Processes, Charles Proteus Steinmetz & Nelson Wax (eds.), Dover, 1954. Réédité dans la collection Phoenix (2003), ASIN 0486495353.
Bibliothèque virtuelle
- (en) Martin Z. Bazant, Random Walks and Diffusion ; cours de mathématiques appliquées donné au MIT, avec des applications à la physique et à la finance.
- (en) Notes de cours 2003.
- (en) Notes de cours 2001.
Marche aléatoire sur une variété riemannienne
- (en) Mark A. Pinsky, Isotropic transport process on a Riemannian manifold, Transaction of the American Mathematical Society 218 (1976), 353-360.
- (en) Nicolas Th. Varopoulos, Brownian motion and random walks on manifolds [PDF], Annales de l'Institut Fourier 34(2) (1984), 243-269.