Loi de Rayleigh
En probabilités et en statistiques, la loi de Rayleigh, est une loi de probabilité à densité. Elle apparaît comme la norme d'un vecteur gaussien bi-dimensionnel dont les coordonnées sont indépendantes, centrées et de même variance. Cette loi de probabilité est baptisée d'après Lord Rayleigh.
Typiquement, la distance Dn à laquelle une particule se trouve de son point de départ, après avoir effectué n pas d'une marche aléatoire symétrique dans le plan, suit approximativement une loi de Rayleigh de paramètre √n. Dans un tout autre domaine, elle est fréquemment utilisée pour décrire l'enveloppe d'un processus de Gauss à bande étroite.
Propriétés
Les moments sont donnés par :
où Γ(z) est la fonction Gamma.
L'espérance et la variance d'une variable aléatoire de Rayleigh X sont les suivantes :
et
Le coefficient d'asymétrie ((en) skewness) est :
La kurtosis est :
La fonction caractéristique est :
où erfi(z) est la fonction d'erreur complexe. La transformée de Laplace est
où erf(z) est la fonction d'erreur.
Estimation du paramètre
Étant donné N variables de Rayleigh indépendantes et de même loi de paramètre σ, l'estimateur du maximum de vraisemblance de σ est
Engendrer des variables de Rayleigh
Étant donné une variable U uniforme sur l'intervalle ]0;1[, la variable
suit la loi de Rayleigh de paramètre σ. Cela provient de la forme de la fonction de répartition, en particulier du théorème de la réciproque, et du fait que 1–U a même loi que U.
Lien avec d'autres lois continues
- suit la loi de Rayleigh si , où et sont deux variables gaussiennes indépendantes, ce qui explique le choix du symbole "σ" pour paramétriser la loi de Rayleigh.
- Si , alors R2 suit la loi du χ² avec deux degrés de liberté: qui est une loi exponentielle de paramètre 1/2.
- Si X suit une loi exponentielle , alors .
- Si , et si les Ri forment une suite de variables indépendantes, alors suit une loi gamma de paramètres N et 2σ2 : .
- La loi de Rice est une généralisation de la loi de Rayleigh.
Lien avec certaines lois discrètes
Marche aléatoire dans le plan
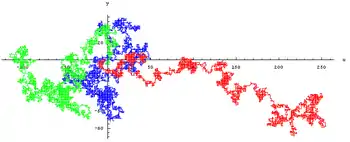
Notons Dn la distance entre la position d'un marcheur au hasard dans le plan, après n pas au hasard, et son point de départ : Dn/√n converge en loi vers la loi de Rayleigh, ce qui signifie qu'en parcourant une distance n, le marcheur ne s'éloigne vraiment de son point de départ que de √n pas approximativement, la convergence vers la loi de Rayleigh permettant de préciser cette approximation.
Distance entre deux points au hasard d'un arbre de Cayley aléatoire
À l'aide de la bijection de Joyal, on peut montrer que la loi de la distance Dn entre deux points au hasard d'un arbre de Cayley aléatoire est donnée, pour par
On peut montrer, par exemple à l'aide du lemme de Scheffé, que Dn/√n converge en loi vers la loi de Rayleigh, ce qui indique que la distance "typique" entre deux points d'un arbre de taille n est de l'ordre de √n.
Points cycliques d'une application
En vertu de la bijection de Joyal, le nombre de points cycliques d'une application ω de dans , suit la même loi que Dn. Ainsi, Cn/√n converge en loi vers la loi de Rayleigh.
Problème des anniversaires
Cette loi discrète apparaît aussi dans des problèmes d'allocations (boules et urnes), dont le fameux paradoxe des anniversaires. Lorsqu'on alloue séquentiellement des boules dans un ensemble de n urnes, avec équiprobabilité, ce qui revient à considérer un univers probabiliste le rang de la première boule à être allouée dans une urne non vide suit la même loi que 2 + Dn Ainsi, Tn/√n converge en loi vers la loi de Rayleigh.
Pour n=365, soit 365 boîtes, s'interprète comme la taille du groupe pour laquelle il devient probable qu'au moins deux membres du groupe ait la même date d'anniversaire (il faut imaginer un groupe dont l'effectif augmente progressivement) : la probabilité que dans un groupe de personnes, toutes les dates d'anniversaire soit différentes, est approximativement
et vaut donc 1/2 pour un groupe d'approximativement (soit 22,5) personnes, ou bien 1/10 pour un groupe d'approximativement (soit 41) personnes. Le calcul exact du premier entier tel que cette probabilité soit plus petite que 1/2 (respectivement 1/10) donne les mêmes résultats : 23 (respectivement 41).
Notes et références
- (en) Eric W. Weisstein, « Loi de Rayleigh », sur MathWorld.
















![{\displaystyle \mathbb {E} [X]=\sigma {\sqrt {\frac {\pi }{2}}}\approx 1{,}253\cdot \sigma \,}](https://img.franco.wiki/i/8f02dacbc39607519a3e7e1b36c877d7c7da14d1.svg)


















![[Y=\sum _{{i=1}}^{N}R_{i}^{2}]\sim \Gamma (N,2\sigma ^{2})](https://img.franco.wiki/i/d22c9a7021f76d74ceb14903ba46c9082b42ae2a.svg)




![[\![1,n]\!]](https://img.franco.wiki/i/b9742260f2c04dfe897a9b8702005a64dcc12a34.svg)
![{\displaystyle \Omega \ =\ [\![1,n]\!]^{\mathbb {N} },\ }](https://img.franco.wiki/i/564ff80110ae28fa66ee05b74bf329a524fc7b34.svg)




