Loi uniforme continue
En théorie des probabilités et en statistiques, les lois uniformes continues forment une famille de lois de probabilité à densité. Une telle loi est caractérisée par la propriété suivante : tous les intervalles de même longueur inclus dans le support de la loi ont la même probabilité. Cela se traduit par le fait que la densité de probabilité d'une loi uniforme continue est constante sur son support.
| Loi uniforme continue de paramètres et | |
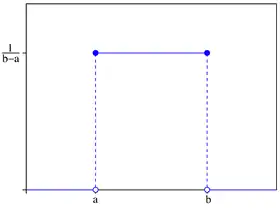 Densité de probabilité | |
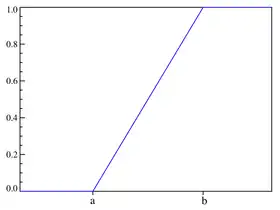 Fonction de répartition | |
| Paramètres | |
|---|---|
| Support | |
| Densité de probabilité | |
| Fonction de répartition | |
| Espérance | |
| Médiane | |
| Mode | |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Entropie | |
| Fonction génératrice des moments | |
| Fonction caractéristique | |
Elles constituent donc une généralisation de la notion d'équiprobabilité dans le cas continu pour des variables aléatoires à densité ; le cas discret étant couvert par les lois uniformes discrètes.
Une loi uniforme est paramétrée par la plus petite valeur et la plus grande valeur que la variable aléatoire correspondante peut prendre. La loi uniforme continue ainsi définie est souvent notée
Les densités associées aux lois uniformes continues sont des généralisations de la fonction rectangle en raison de leurs formes.
Caractérisation
Fonction génératrice des moments
La fonction génératrice des moments de la loi est :
Elle permet de calculer tous les moments non centrés, mk :
Ainsi, pour une variable aléatoire suivant la loi l'espérance est m1 = (a + b)/2, et la variance est m2 − m12 = (b − a)2/12.
Fonction génératrice des cumulants
Pour n ≥ 2, le n-ième cumulant de la loi uniforme continue sur l'intervalle [0, 1] est bn/n, où bn est le n-ième nombre de Bernoulli.
Propriétés
Statistiques d'ordre
Soit X1, ..., Xn un échantillon i.i.d. issu de la loi Soit X(k) la k-ième statistique d'ordre de l'échantillon. Alors la distribution de X(k) est une loi bêta de paramètres k et n − k + 1.
L'espérance est :
Ce fait est utile lorsqu'on construit une droite de Henry.
La variance est :
Aspect uniforme
La probabilité qu'une variable uniforme tombe dans un intervalle donné est indépendante de la position de cet intervalle, mais dépend seulement de sa longueur à condition que cet intervalle soit inclus dans le support de la loi. Ainsi, si X suit la loi et si est un sous-intervalle de [a, b], avec fixé, alors :
qui est indépendant de x. Ce fait motive la dénomination de cette loi.
Loi uniforme standard
Le cas particulier a = 0 et b = 1 donne naissance à la loi uniforme standard, notée Il faut noter le fait suivant : si u1 est distribué selon une loi uniforme standard, alors c'est aussi le cas pour u2 = 1 – u1.
Loi uniforme sur une partie borélienne
À toute partie A de borélienne, dont la mesure de Lebesgue λ(A) est finie et strictement positive, on associe une loi de probabilité, appelée loi uniforme sur A, de densité de probabilité ƒ définie, pour tout par :
où χA est la fonction indicatrice (ou caractéristique), notée aussi 𝟙A, de l'ensemble A. La densité est donc nulle à l'extérieur de A, mais égale à la constante 1⁄λ(A) sur A.
Cette page traite principalement du cas particulier où d = 1 et où A est un intervalle [a, b] de
Transport et invariance
Condition suffisante — La loi de la variable aléatoire Y = T(X), image par une transformation T d'une variable X uniforme sur une partie A de est encore la loi uniforme sur T(A) si T est, à un ensemble négligeable près, injective et différentiable, et si, presque partout sur A, la valeur absolue du jacobien de T est constante.
- Si T est affine et bijective, alors Y suit la loi uniforme sur T(A).
- En particulier, si T est une isométrie de laissant A globalement invariant, alors Y a même loi que X.
- Par exemple, une isométrie de laisse invariante la loi uniforme sur B(O, 1], la boule unité centrée en l'origine, à condition de laisser l'origine invariante (donc de laisser B(O, 1] globalement invariante).
- Autre exemple d'isométrie : si U est uniforme sur [0, 1], alors 1 – U l'est aussi.
- Notons la partie fractionnaire de Les fonctions et ne sont ni injectives ni différentiables sur tout [0, 1], mais satisfont les hypothèses énoncées plus haut, avec T([0, 1[) = [0, 1[. En conséquence, si alors et ont même loi que En sortant un peu du cadre de cette page, et en notant M(x) le point du cercle trigonométrique ayant pour affixe on peut voir M(U) comme un point tiré au hasard uniformément sur le cercle trigonométrique. Les points et respectivement sont alors obtenus par rotation d'angle 2πa et par symétrie par rapport à la droite d'angle directeur πa respectivement, qui sont des isométries laissant le cercle unité globalement invariant. Donc ces points suivent aussi la loi uniforme sur le cercle unité. Cela traduit une propriété très particulière de la loi uniforme : elle est la mesure de Haar de
Conséquence — Si la suite est une suite de variables aléatoires indépendantes et uniformes sur [0, 1], et si alors la suite est une suite de variables aléatoires indépendantes et uniformes sur [0, 1].
Il peut sembler surprenant que les variables et par exemple, soient indépendantes, alors qu'elles dépendent toutes deux de manière cruciale des variables et C'est une conséquence particulière de la propriété d'invariance de la loi uniforme : par exemple, étant la mesure de Haar de elle est idempotente pour la convolution.
Distributions associées
Le théorème suivant[1] stipule que toutes les distributions sont liées à la loi uniforme :
Théorème de la réciproque — Pour une variable aléatoire de fonction de répartition on note sa réciproque généralisée, définie, pour tout par :
Si désigne une variable aléatoire réelle uniforme sur alors a pour fonction de répartition
Ainsi, pour obtenir des tirages (indépendants) selon la loi répartie par il suffit d'appliquer l'inverse de à des tirages (indépendants) uniformes sur
Voici quelques exemples d’application de ce théorème
- suit la loi exponentielle de paramètre
- Y = 1 – U1/n suit la loi bêta de paramètres 1 et n. Ceci implique que la loi uniforme standard est un cas particulier de la loi bêta, de paramètres 1 et 1.
On trouvera un tableau plus complet ici. Par ailleurs, l'art d'engendrer des variables aléatoires de lois arbitraires, par exemple à l'aide de variables uniformes, est développé dans Non-Uniform Random Variate Generation, de Luc Devroye, édité chez Springer, disponible sur le web[2].
Inférence statistique
Estimation de l'un des paramètres lorsque l'autre est connu
Cette section décrit l'estimation de la borne supérieure de la distribution au vu d'un échantillon de individus, la borne inférieure étant connue.
Estimateur sans biais de variance minimale
Pour une loi uniforme sur avec inconnu, l'estimateur sans biais de valeur minimale (en) pour le maximum est donné par :
où est le maximum de l'échantillon et la taille de l'échantillon, échantillonné sans remise (bien que cette précision n'a aucune incidence dans le cas uniforme).
On obtient cette valeur par un raisonnement similaire au cas discret. Ce problème peut être vu comme un cas simple d'estimation de l'espacement maximal (en). Il est connu sous le nom de Problème du char d'assaut allemand, par son application d'estimation maximale de la production des chars d'assaut allemands pendant la Seconde Guerre mondiale.
Estimateur par maximum de vraisemblance
L'estimateur par maximum de vraisemblance est :
où est la valeur maximum dans l'échantillon, qui est aussi la statistique d'ordre maximale de l'échantillon.
Estimateur par la méthode des moments
L'estimateur par la méthode des moments est :
où est la moyenne de l'échantillon.
Estimation du milieu
Le milieu de l'intervalle de la loi uniforme est à la fois la moyenne et la médiane de cette loi. Bien que la moyenne et la médiane de l'échantillon sont des estimateurs sans biais du milieu, ils ne sont pas aussi efficaces que le milieu de gamme de l'échantillon, i.e. la moyenne arithmétique du maximum et du minimum de l'échantillon, qui est l'estimateur sans biais de variance minimale du milieu (et aussi l'estimateur par maximum de vraisemblance).
Pour le maximum
On considère X1, X2, ..., Xn un échantillon de où L est la valeur maximum dans la population. Alors X(n) = max( X1, X2, ..., Xn ) a la densité de Lebesgue-Borel[3]
où est la fonction caractéristique (ou indicatrice) de
L'intervalle de confiance est mathématiquement incorrect, car ne peut être résolu pour sans information sur On peut cependant résoudre
- pour pour tout inconnu mais valide ;
on peut alors choisir le plus petit possible vérifiant la condition ci-dessus. On note que la longueur de l'intervalle dépend de la variable aléatoire
Estimation simultanée des deux paramètres
Cette section décrit l'estimation des deux bornes de la distribution uniforme continue au vu d'un échantillon de individus.
Soient et les estimateurs respectifs des bornes inférieure et supérieure de la distribution mère, construits sur la base de l'échantillon contenant les modalités de la variable aléatoire issues de la distribution
La méthode du maximum de vraisemblance aboutit à la sélection des minimum et maximum empiriques :
Ce couple d'estimateurs est biaisé : la probabilité qu'un -échantillon capture le minimum ou le maximum permis par la distribution mère étant quasi-nulle, la moyenne d'un grand nombre d'observations sur de tels -échantillons ne converge pas vers les bornes de ladite distribution mère :
La démonstration est produite plus bas.
Loi de distribution régissant ces estimateurs biaisés
Les densités de probabilité sont notées en minuscules (par ex. ), les fonctions de répartition sont notées en majuscules (par ex. ).
Densité de probabilité associée au couple d'estimateurs biaisés
Lois marginales régissant les minimum et maximum empiriques
Concernant l'estimateur de la borne inférieure
Par une démonstration similaire, on obtient pour l'estimateur de la borne supérieure :
Convergence de ces estimateurs
La définition de la convergence d'un estimateur est donnée dans le document référencé [4].
Concernant l'estimateur de la borne inférieure ( sur un n-échantillon) : car aucune valeur inférieure à a ne peut être observée. Donc :
Une démonstration similaire s'applique pour l'estimateur de la borne supérieure.
forme donc un couple d'estimateurs convergents.
Biais de ces estimateurs
Lorsque l'on multiplie les échantillons (de taille donnée), la moyenne des observations ne tend pas vers le couple de bornes de la distribution mère :
Ces deux estimateurs ne sont qu'asymptotiquement sans biais[4], i.e. lorsque la taille de l'échantillon tend vers l'infini.
Recherche d'estimateurs sans biais
Le couple d'estimateurs défini ci-dessous est sans biais[5] :
Le calcul de ces estimateurs (avec ou sans biais) ne nécessite pas la connaissance des paramètres de la distribution mère.
Les lois de distribution qui régissent le couple d'estimateurs sans biais sont plus complexes à déterminer. Le document [5] donne les lois suivantes :
Densité de probabilité associée au couple d'estimateurs sans biais
Lois marginales régissant chacun des deux estimateurs sans biais
Sachant que la variable admet comme support l'intervalle :
Sachant que la variable admet comme support l'intervalle :
Intervalle de pari
On considère ici :
- une loi mère uniforme donnée et connue,
- le couple d'estimateurs avec biais formé par le minimum et le maximum empiriques déterminés sur un -échantillon.
Les estimateurs considérés sont ceux avec biais car :
- leurs lois de distribution sont simples à manipuler ;
- le document référencé [5] montre que construire des intervalles de pari à partir des estimateurs sans biais n'aboutit pas in fine à des intervalles plus réduits pour un niveau de confiance donné, et en explique la raison.
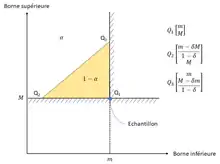
On cherche à connaître comment se répartissent les n-échantillons possibles formés à partir de la distribution mère , en plaçant dans le plan :
- sur l'axe des abscisses, la borne inférieure de la distribution mère et les minima empiriques des échantillons ;
- sur l'axe des ordonnées, la borne supérieure de la distribution mère et les maxima empiriques des échantillons.
On note :

La distribution mère et la construction des estimateurs imposent la hiérarchie suivante : Les échantillons issus de cette loi mère sont tous situés à l'intérieur du triangle rectangle formé par la droite , la droite et la première bissectrice (cf. figure ci-contre).
Un bon échantillon (i.e. un échantillon représentatif de sa population mère) se caractérise par :
- un minimum empirique proche de
- et un maximum empirique proche de
Le risque de pari associé à un échantillon est défini par la probabilité de trouver un échantillon plus mauvais que lui, i.e. présentant :
- un minimum empirique supérieur ou égal à
- ou un maximum empirique inférieur ou égal à
Intervalle de pari sur le minimum empirique

L'expérimentateur choisit son risque de pari . Le risque de pari sur le minimum empirique est défini par l'équation suivante :
La surface de pari sur le minimum empirique au niveau de confiance rassemble les échantillons qui vérifient : et .
Intervalle de pari sur le maximum empirique

De façon similaire, le risque de pari sur le maximum empirique est défini par l'équation suivante :
La surface de pari sur le maximum empirique au niveau de confiance rassemble les échantillons qui vérifient : et .
Surface de pari sur les deux bornes
La surface de pari est celle qui capture la proportion des échantillons formés à partir d'une population mère donnée et connue.

Le problème dépend de la forme que l'on aura choisi de donner à cette surface, qui peut être un carré, un triangle, un quart de cercle, ... On choisit ici un triangle rectangle, de sommet et dont l'hypoténuse est parallèle à la première bissectrice (cf. figure ci-contre). La raison est que la densité de probabilité associée au couple est constante le long d'un lieu . Ceci permet de découper l'espace suivant une ligne iso-densité, minimisant ainsi la surface de pari pour capturer un effectif donné.
Les variables réduites classiques pour les distributions uniformes sont introduites afin de simplifier les calculs qui suivent :
Les relations de conversion du domaine réel en domaine réduit sont données par le tableau ci-dessous :
| Échantillon {m ; M} à population {a ; b} donnée | Représentation adimensionnée | Population {a ; b} à échantillon {m ; M} donné |
|---|---|---|
Exprimée dans le plan des coordonnées réduites, la surface pari au niveau de confiance est constituée par l'intérieur du triangle rectangle de sommets :
La marge réduite est reliée au risque de pari par l'équation suivante :

L'équation liant la marge réduite au risque de pari peut être résolue par la méthode du point fixe : la suite définie ci-dessous converge rapidement vers la solution, même avec une initialisation forfaitaire :

Le lieu des solutions est tracé ci-contre, en fonction de l'effectif de l'échantillon et du risque de pari .
Replacée dans le plan des coordonnées correspondant au problème réel de l'expérimentateur, la surface pari au niveau de confiance est constituée par l'intérieur du triangle rectangle de sommets :
Surface de confiance
Le point de vue est inversé par rapport à la section précédente :
- le n-échantillon est connu, et le couple des minimum et maximum empiriques obtenus est ;
- on veut connaître quelles populations mères auraient pu générer cet échantillon, au niveau de confiance choisi par l'expérimentateur.
Il s'agit donc de recenser les populations mères qui contiennent l'échantillon en question dans leurs surfaces de pari respectives au niveau de confiance .
L'intégrale calculée lors de la démonstration qui établit la surface de pari en coordonnées réduites reste inchangée, quelles que soient les raisons qui font varier ces coordonnées réduites :
- les variations du couple à population mère fixée,
- ou bien les variations des bornes de la population mère à échantillon fixé
La surface de confiance est obtenue par déréduction de la surface établie en coordonnées pour le niveau de confiance , en cherchant à échantillon fixé. Cette surface de confiance est constituée par l'intérieur du triangle rectangle de sommets :
Applications
En statistiques, lorsqu'une valeur p (p-value) est utilisée dans une procédure de test statistique pour une hypothèse nulle simple, et que la distribution du test est continue, alors la valeur p est uniformément distribuée selon la loi uniforme sur [0, 1] si l'hypothèse nulle est vérifiée.
Obtenir des réalisations de la loi uniforme
La plupart des langages de programmation fournissent un générateur de pseudo-nombres aléatoires, dont la distribution est effectivement la loi uniforme standard.
Si u est U(0, 1), alors v = a + (b − a)u suit la loi U(a, b).
Obtenir des réalisations d'une loi continue quelconque
D'après le théorème cité plus haut, la loi uniforme permet en théorie d'obtenir des tirages de toute loi continue à densité. Il suffit pour cela d'inverser la Fonction de répartition de cette loi, et de l'appliquer à des tirages de la loi uniforme standard. Malheureusement, dans bien des cas pratiques, on ne dispose pas d'une expression analytique pour la fonction de répartition; on peut alors utiliser une inversion numérique (coûteuse en calculs) ou des méthodes concurrentes, comme la Méthode de rejet.
Le plus important exemple d'échec de la méthode de la transformée inverse est la Loi normale. Toutefois, la Méthode de Box-Muller fournit une méthode pratique pour transformer un échantillon uniforme en un échantillon normal, et ce de manière exacte[6].
Permutations aléatoires uniformes et loi uniforme
Des mathématiciens comme Luc Devroye ou Richard P. Stanley ont popularisé l'utilisation de la loi uniforme sur [0, 1] pour l'étude des permutations aléatoires (tailles des cycles, nombres eulériens, analyse d'algorithmes de tri comme le tri rapide, par exemple).
Construction d'une permutation aléatoire uniforme à l'aide d'un échantillon de loi uniforme
Soit une suite de variables aléatoires i.i.d. uniformes sur [0, 1], définies sur un espace probabilisé (par exemple, définies sur muni de sa tribu des boréliens et de sa mesure de Lebesgue, par ou, de manière équivalente, par ). Pour tout entier k compris entre 1 et n, posons
Ainsi, s'interprète comme le rang de dans l'échantillon, une fois celui-ci rangé dans l'ordre croissant.
Proposition — L'application est une permutation aléatoire uniforme.
La proposition ci-dessus reste vérifiée si la distribution de probabilité commune aux variables possède une densité, quelle qu'elle soit, et non pas seulement pour la densité uniforme. On peut même se contenter de variables i.i.d. dont la loi est diffuse (sans atomes) modulo une modification mineure de la démonstration. Cependant la loi uniforme est particulièrement commode pour diverses applications.
Nombres de descentes d'une permutation aléatoire, et nombres eulériens
Soit le nombre de descentes d'une permutation tirée au hasard uniformément dans Bien sûr,
où A(n,k) désigne le nombre de permutations de possédant exactement k descentes. A(n,k) est appelé nombre eulérien. Posons
On a alors[7]
Théorème (S. Tanny, 1973) — De manière équivalente,
ou bien
Il en découle immédiatement un théorème central limite pour via le théorème de Slutsky.
Notes et références
- Voir l'article détaillé ici.
- La version pdf (libre et autorisée) de (en) Luc Devroye, Non-Uniform Random Variate Generation, New York, Springer-Verlag, , 1re éd. (lire en ligne) est disponible, ainsi qu'un récit humoristique des démêlés de Luc Devroye avec son éditeur.
- (en) KN Nechval, NA Nechval NA, EK Vasermanis et VY Makeev, « Constructing shortest-length confidence intervals », Transport and Telecommunication, vol. 3, no 1, , p. 95-103 (lire en ligne)
- Jean-Jacques Ruch, « Statistiques : estimation », sur www.google.fr (consulté le )
- Christophe Boilley, « Estimation des bornes d'une loi uniforme », sur Classeur numérique de Christophe Boilley, (consulté le )
- Plus exactement, la méthode nécessite deux tirages indépendants U(0, 1) pour fournir deux tirages normaux indépendants.
- voir (en) S. Tanny, « A probabilistic interpretation of the Eulerian numbers », Duke Math. J., vol. 40, , p. 717-722 ou bien (en) R.P. Stanley, « Eulerian partitions of a unit hypercube », Higher Combinatorics, Dordrecht, M. Aigner, ed., Reidel, .



![[a,b]](https://img.franco.wiki/i/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)



![{\displaystyle {\text{toute valeur dans }}[a,b]}](https://img.franco.wiki/i/f34a2fe5014999ede546ec01c96b7b0eeb13da1f.svg)










![{\displaystyle M_{X}=\mathbb {E} [{\rm {e}}^{tX}]={\frac {{\rm {e}}^{tb}-{\rm {e}}^{ta}}{t(b-a)}}.}](https://img.franco.wiki/i/7d53eb38a0d1d178cbb5512ffbae4aa6a0ff0732.svg)





![{\displaystyle \mathbb {E} [X_{(k)}]={k \over n+1}.}](https://img.franco.wiki/i/a55305925bc4078616d4b35b4539b3ed7ca76a55.svg)
![{\displaystyle \mathbb {V} [X_{(k)}]={k(n-k+1) \over (n+1)^{2}(n+2)}.}](https://img.franco.wiki/i/2230cdd77f9678a3b912cad0f21e7f994f649b33.svg)

![{\displaystyle [x,x+\ell ]}](https://img.franco.wiki/i/884130fbd3c593f4108f325e7ce5f5724e808872.svg)

![{\displaystyle \mathbb {P} {\big (}X\in [x,x+\ell ]{\big )}=\int _{x}^{x+\ell }{\frac {\mathrm {d} y}{b-a}}={\frac {\ell }{b-a}},}](https://img.franco.wiki/i/e69f5869e4d030cad3a2d76b5584b2311b7be3cc.svg)





































![{\displaystyle \omega \in \ ]0,1[,}](https://img.franco.wiki/i/c8dc9699e0c63e10e85c1e764c3d855904b9ac65.svg)


![{\displaystyle [0,1],}](https://img.franco.wiki/i/971caee396752d8bf56711f55d2c3b1207d4a236.svg)



![{\displaystyle [0,1].}](https://img.franco.wiki/i/8786b5ef9daedb24adb59e7825c4096d99a99648.svg)






![{\displaystyle [0,b]}](https://img.franco.wiki/i/ba22e25e8f8604f012c599a7d4962562c4bb3f02.svg)







![{\displaystyle {\mathcal {U}}_{[0,L]},}](https://img.franco.wiki/i/20a95e677457c689e77d9414f3e57cfce62214ee.svg)

![{\displaystyle \mathrm {f} (t)=n{\frac {1}{L}}\left({\frac {t}{L}}\right)^{n-1}1\!\!1_{[0;L]}(t)=n{\frac {t^{n-1}}{L^{n}}}1\!\!1_{[0;L]}(t),}](https://img.franco.wiki/i/678309e88916fedd510a581a8e61d83313557e21.svg)
![{\displaystyle 1\!\!1_{[0,L]}}](https://img.franco.wiki/i/79cff43b95a58c16bc9a5d97be265cabd4a635bb.svg)
![{\displaystyle [0,L].}](https://img.franco.wiki/i/865dd4a189168d3c11e65b12bbb7880568652e1f.svg)
![{\displaystyle \mathbb {P} ([{\hat {\theta }},{\hat {\theta }}+\varepsilon ]\ni \theta )\geq 1-\alpha }](https://img.franco.wiki/i/9344036aa6f62940b92d8cd94e2165745174e68a.svg)


![{\displaystyle \mathbb {P} ([{\hat {\theta }},{\hat {\theta }}(1+\varepsilon )]\ni \theta )\geq 1-\alpha }](https://img.franco.wiki/i/d2ca875a40cfebafdadef29fcb309697bf2250d4.svg)


![{\displaystyle [{\hat {\theta }},{\hat {\theta }}(1+\varepsilon )]}](https://img.franco.wiki/i/fb31d7d56ef14522fbfce34b9d996c2dbd9f7699.svg)


























![{\displaystyle \forall x\in [a,b]\;{\begin{cases}d\mathbb {P} \,(x\leq {\hat {a}}\leq x+dx)&=&f_{\hat {a}}(x)\,dx&=&{\frac {n}{b-a}}\,{\Bigl (}{\frac {b-x}{b-a}}{\Bigr )}^{n-1}\,dx\\\mathbb {P} \,({\hat {a}}\leq x)&=&F_{\hat {a}}(x)&=&1-{\Bigl (}{\frac {b-x}{b-a}}{\Bigr )}^{n}.\end{cases}}}](https://img.franco.wiki/i/b8e1392848ebd667ebf8e5e676ea711ff450540f.svg)




![{\displaystyle {\hat {b}}\in \left[{\hat {a}},b\right]}](https://img.franco.wiki/i/665985020bd5e7e2945dbcd01b9473f4978e8ada.svg)
![{\displaystyle {\hat {a}}\in \left[a,{\hat {b}}\right]}](https://img.franco.wiki/i/c88c4e35f826e9ba86ccd5a2d3f1a972d6cdb06b.svg)

![{\displaystyle \forall x\in [a,b]\;{\begin{cases}\mathrm {d} \mathbb {P} \,(x\leq {\hat {b}}\leq x+dx)&=&f_{\hat {b}}(x)\,\mathrm {d} x&=&{\frac {n}{b-a}}\,\left({\frac {x-a}{b-a}}\right)^{n-1}\,\mathrm {d} x\\\mathbb {P} \,({\hat {b}}\leq x)&=&F_{\hat {b}}(x)&=&\left({\frac {x-a}{b-a}}\right)^{n}.\end{cases}}}](https://img.franco.wiki/i/2212a37fbecce39aca5eb16720c24b64261205e1.svg)


![{\displaystyle \mathbb {P} \,(|{\hat {a}}_{n}-a|>\varepsilon )=\left({\frac {b-a-\varepsilon }{b-a}}\right)^{n}=\left(1-{\frac {\varepsilon }{b-a}}\right)^{n}{\xrightarrow[{n\rightarrow +\infty }]{}}\,0.}](https://img.franco.wiki/i/17c1dabf8e95e8f510651eaa284c666adbc1ae49.svg)













![{\displaystyle \left[{\frac {n\,a-b}{n-1}}\,;\,b\right]}](https://img.franco.wiki/i/eb6521dbc4bc3aca61ee2f2035ece63b48fdf535.svg)
![{\displaystyle {\begin{cases}\forall x\leq a&d\mathbb {P} \,\left(x\leq {\hat {\hat {a}}}\leq x+dx\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left[\left(b-x\right)^{n-1}-n^{n-1}\left(a-x\right)^{n-1}\right]\,dx\\\forall x\geq a&d\mathbb {P} \,\left(x\leq {\hat {\hat {a}}}\leq x+dx\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left(b-x\right)^{n-1}\,dx.\end{cases}}}](https://img.franco.wiki/i/f99203a9183d783fda92b96524875b2d4b7f3503.svg)

![{\displaystyle \left[a\,;\,{\frac {n\,b-a}{n-1}}\right]}](https://img.franco.wiki/i/d66c7ad48f82b161e824707506492c68d3a358b2.svg)
![{\displaystyle {\begin{cases}\forall y\leq b&d\mathbb {P} \,\left(y\leq {\hat {\hat {b}}}\leq y+dy\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left(y-a\right)^{n-1}\,dy\\\forall y\geq b&d\mathbb {P} \,\left(y\leq {\hat {\hat {b}}}\leq y+dy\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left[\left(y-a\right)^{n-1}-n^{n-1}\left(y-b\right)^{n-1}\right]\,dy.\end{cases}}}](https://img.franco.wiki/i/3303bc4716c3623f70fefd2b3a0792eca4e2784c.svg)














![{\displaystyle \alpha =\mathbb {P} \,\left({\hat {a}}\geq m\;\forall {\hat {b}}\in \left[{\hat {a}}\,;\,b\right]\right)=\left({\frac {b-m}{b-a}}\right)^{n}\Rightarrow \,m_{1-\alpha }=b-(b-a)\cdot \alpha ^{\frac {1}{n}}}](https://img.franco.wiki/i/5572b05bd7c8f0468d37d0301eb0d91838de8b05.svg)

![{\displaystyle {\hat {a}}\in [a\,;m_{1-\alpha }]}](https://img.franco.wiki/i/1a45ef8e8a5d39924c7bbaa3e6cf4b8efe3626eb.svg)
![{\displaystyle {\hat {b}}\in [{\hat {a}}\,;b]}](https://img.franco.wiki/i/38ce0398b54766836dd173f27d0bda23167a2983.svg)
![{\displaystyle \alpha =\mathbb {P} \,\left({\hat {b}}\leq M\;\forall {\hat {a}}\in \left[a\,;{\hat {b}}\right]\right)=\left({\frac {M-a}{b-a}}\right)^{n}\Rightarrow \,M_{1-\alpha }=a+(b-a)\cdot \alpha ^{\frac {1}{n}}}](https://img.franco.wiki/i/8ee900c4d556cf31335f489286fcf069df90296e.svg)
![{\displaystyle {\hat {b}}\in [M_{1-\alpha }\,;b]}](https://img.franco.wiki/i/b5e8f5669397a8f91199b271b99abba92e9c29cf.svg)
![{\displaystyle {\hat {a}}\in [a\,;{\hat {b}}]}](https://img.franco.wiki/i/618eac6e72030279a61af70316ef3f0f8c26419e.svg)







![{\displaystyle {\begin{cases}m&\in &\left[a\,;\,M\right]\\M&\in &\left[m\,;\,b\right]\end{cases}}}](https://img.franco.wiki/i/74b3bb648656e859544df53a2182cec08a7a30d1.svg)
![{\displaystyle {\begin{cases}a&\in &\left]-\infty \,;m\right]\\b&\in &\left[M\,;+\infty \right[\end{cases}}}](https://img.franco.wiki/i/405532556207462e157dcdbcbb6c57aadf3e66c8.svg)















![{\displaystyle \left(1-\delta \right)^{n-1}\,\left[1+\left(n-1\right)\delta \right]=\alpha }](https://img.franco.wiki/i/d2a6faf5119e20237e98b41adab76cdd2eded2a2.svg)




![{\displaystyle 1-\left(1-\delta \right)^{n-1}\,\left[1+\left(n-1\right)\delta \right]=1-\alpha }](https://img.franco.wiki/i/fd773c714049ab1b73f4aaa787e8ecab9f9c80a1.svg)










![{\displaystyle \Omega =[0,1]^{n}}](https://img.franco.wiki/i/876ee1f948790f953a4fb0e1607b4e67412daa8d.svg)




















































