Méthode de la transformée inverse

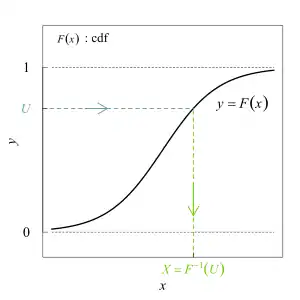
Cette méthode repose sur le principe suivant, parfois connu sous le nom de théorème de la réciproque : soient F une fonction de répartition, Q la fonction quantile associée, et U une variable uniforme sur [0, 1]. Alors, la variable aléatoire X = Q(U) a pour fonction de répartition F. Ainsi, pour échantillonner une variable aléatoire de loi donnée, il suffit de savoir échantillonner des variables uniformes sur [0, 1] et de pouvoir calculer la fonction quantile de la loi souhaitée.

Le nom méthode de la transformée inverse provient du fait que la fonction quantile n'est autre que l'inverse généralisé à gauche de la fonction de répartition :

${\displaystyle Q(u)=\inf \left\{x:F(x)\geqslant u\right\}}$

En particulier, si la fonction de répartition F est continue et strictement croissante, alors elle est bijective et Q = F⁻¹ est sa bijection réciproque.

Pour certaines lois, on sait inverser la fonction de répartition F, comme le montre la liste suivante :

	Fonction de répartition F	Fonction de répartition inverse F−1(U)
loi exponentielle de paramètre λ	${\displaystyle F(x)=\left\{{\begin{matrix}1-\mathrm {e} ^{-\lambda x}&{\text{si}}\;x\geqslant 0\\0&{\text{si}}\;x<0\end{matrix}}\right.}$	${\displaystyle -{\tfrac {1}{\lambda }}\ln(1-U)}$
loi de Cauchy standard	${\displaystyle F(x)={\frac {1}{\pi }}\arctan(x)+{\frac {1}{2}}}$	${\displaystyle \tan(\pi U)}$
loi logistique standard	${\displaystyle F(x)={\frac {1}{1+\mathrm {e} ^{-x}}}}$	${\displaystyle -\ln \left({\tfrac {U}{1-U}}\right)}$
loi de Laplace	${\displaystyle F(x)=0,5(1+\mathrm {sgn} (x)[1-\mathrm {e} ^{-|x|}])}$	${\displaystyle -\mathrm {sgn} (U)\ln(1-2|U|)}$

Ainsi, par exemple, échantillonner une variable selon la loi exponentielle de paramètre λ :

1. on tire un nombre U uniformément sur [0, 1]
2. on calcule ${\displaystyle -{\frac {1}{\lambda }}\ln(1-U)}$.

A noter ici que, puisque U suit la loi uniforme sur [0, 1] si et seulement si 1 - U suit la loi uniforme sur [0, 1], on pourrait également utiliser ${\displaystyle -{\tfrac {1}{\lambda }}\ln(U)}$. Toutefois, pour des raisons de précision numérique, on utilisera généralement ${\displaystyle -{\tfrac {1}{\lambda }}\mathrm {log1p} (-U)}$, la fonction ${\displaystyle \mathrm {log1p} }$ qui à x associe ln(1 + x) étant implémentée dans de nombreux langages de programmation.

Dans le cas général, on ne sait pas inverser la fonction de répartition F de façon analytique, c'est-à-dire qu'on ne dispose pas d'une formule explicite donnant, pour u appartenant à [0, 1], x tel que F(x) = u. Il faut alors résoudre l'équation F(x) = u numériquement, en utilisant au choix une fonction tabulée, la méthode de dichotomie, la méthode de la fausse position, la méthode de la sécante ou encore la méthode de Newton.

La plupart des langages de programmation permettant de produire des nombres pseudo-aléatoires de distribution uniforme, il suffit de calculer l'antécédent des nombres tirés selon la fonction de répartition F.

• Aléatoire
• Pseudo-aléatoire
• Générateur de nombres aléatoires
• Générateur de nombres pseudo-aléatoires
• Méthode de rejet
• Cette méthode est aussi importante sur le plan théorique. Voir en particulier le Théorème de la réciproque dans l'article Fonction de répartition.

• (en) Luc Devroye, Non-Uniform Random Variate Generation, New York, Springer-Verlag, 1986 (lire en ligne)