Méthode de Newton

En analyse numérique, la méthode de Newton ou méthode de Newton-Raphson[1] est, dans son application la plus simple, un algorithme efficace pour trouver numériquement une approximation précise d'un zéro (ou racine) d'une fonction réelle d'une variable réelle. Cette méthode doit son nom aux mathématiciens anglais Isaac Newton (1643-1727) et Joseph Raphson (peut-être 1648-1715), qui furent les premiers à la décrire pour la recherche des solutions d'une équation polynomiale. Thomas Simpson (1710-1761) élargit considérablement le domaine d'application de l'algorithme en montrant, grâce à la notion de dérivée, comment on pouvait l'utiliser pour calculer une solution d'une équation non linéaire, pouvant ne pas être un polynôme, et d'un système formé de telles équations.

Une itération de la méthode de Newton.

Présentation

Sous sa forme moderne, l'algorithme peut être présenté brièvement comme suit : à chaque itération, la fonction dont on cherche un zéro est linéarisée en l'itéré (ou point) courant et l'itéré suivant est pris égal au zéro de la fonction linéarisée. Cette description sommaire indique qu'au moins deux conditions sont requises pour la bonne marche de l'algorithme : la fonction doit être dérivable aux points visités (pour pouvoir y linéariser la fonction) et les dérivées ne doivent pas s'y annuler (pour que la fonction linéarisée ait un zéro) ; s'ajoute à ces conditions la contrainte forte de devoir prendre le premier itéré assez proche d'un zéro régulier de la fonction (i.e., en lequel la dérivée de la fonction ne s'annule pas), pour que la convergence du processus soit assurée.

L'intérêt principal de l'algorithme de Newton est sa convergence quadratique locale. En termes imagés mais peu précis, cela signifie que le nombre de chiffres significatifs corrects des itérés double à chaque itération, asymptotiquement. Comme le nombre de chiffres significatifs représentables par un ordinateur est d’environ 15 chiffres décimaux (sur un ordinateur qui respecte la norme IEEE-754), on peut simplifier grossièrement les propriétés de convergence de l'algorithme de Newton en disant que, soit il converge en moins de 10 itérations, soit il diverge. En effet, si l'itéré initial n'est pas pris suffisamment proche d'un zéro, la suite des itérés générée par l'algorithme a un comportement erratique, dont la convergence éventuelle ne peut être que le fruit du hasard (un des itérés est par chance proche d'un zéro).

L'importance de l'algorithme a incité les numériciens à étendre son application et à proposer des remèdes à ses défauts. Par exemple, l'algorithme permet également de trouver un zéro d'une fonction de plusieurs variables à valeurs vectorielles, voire définie entre espaces vectoriels de dimension infinie ; la méthode conduit d'ailleurs à des résultats d'existence de zéro (utilisés dans certaines preuves du théorème des fonctions implicites, les théorèmes de Kantorovitch). On peut aussi l'utiliser lorsque la fonction est différentiable dans un sens plus faible (fonction différentiable par morceaux, B-différentiable, semi-lisse, obliquement différentiable, etc), ainsi que pour résoudre des systèmes d'inégalité non linéaire, des problèmes d'inclusion fonctionnelle, d'équations différentielles ou aux dérivées partielles, d’inéquations variationnelles, de complémentarité, etc. On a également mis au point des techniques de globalisation de l'algorithme, lesquelles ont pour but de forcer la convergence des suites générées à partir d'un itéré initial arbitraire (non nécessairement proche d'un zéro), comme la recherche linéaire et les régions de confiance agissant sur une fonction de mérite (souvent la fonction de moindres-carrés). Dans les versions dites inexactes ou tronquées, on ne résout le système linéaire à chaque itération que de manière approchée. Enfin, la famille des algorithmes de quasi-Newton propose des techniques permettant de se passer du calcul de la dérivée de la fonction. Toutes ces améliorations ne permettent toutefois pas d'assurer que l'algorithme trouvera un zéro existant, quel que soit l'itéré initial.

Appliqué à la dérivée d'une fonction réelle, cet algorithme permet d'obtenir des points critiques (i.e., des zéros de la fonction dérivée). Cette observation est à l'origine de son utilisation en optimisation sans ou avec contraintes.

Éléments d'histoire

John Wallis.

Isaac Newton.

La méthode de Newton fut décrite par le mathématicien anglais Isaac Newton dans De analysi per aequationes numero terminorum infinitas, écrit en 1669 et publié en 1711 par William Jones. Elle fut à nouveau décrite dans De metodis fluxionum et serierum infinitarum (De la méthode des fluxions et des suites infinies), écrit en 1671, traduit et publié sous le titre Methods of Fluxions en 1736 par John Colson. Toutefois, Newton n'appliqua la méthode qu'aux seuls polynômes. Comme la notion de dérivée et donc de linéarisation n'était pas définie à cette époque, son approche diffère de celle décrite dans l'introduction : Newton cherchait à affiner une approximation grossière d'un zéro d'un polynôme par un calcul polynomial.

L'exemple que Newton donne[2] est celui du calcul de la racine réelle de l'équation cubique

$x^{3}-2x-5=0$ ,

en prenant comme itéré initial le point $x 1 = 2$ . qui diffère de moins de $0,1$ de la vraie valeur de l'unique racine réelle. Il écrit alors $x = 2 + d 1$ , où $d 1$ est donc l'accroissement à donner à $2$ pour obtenir la racine $x$ . Il remplace $x$ par $2 + d 1$ dans l'équation, qui devient

$d_{1}^{3}+6\,d_{1}^{2}+10\,d_{1}-1=0$

et dont il faut trouver la racine pour l'ajouter à $2$ . Il néglige $d 13 + 6 d 12$ à cause de sa petitesse (on suppose que $| d 1 | << 1$ ), si bien qu'il reste $10 d 1 - 1 = 0$ ou $d 1 = 0,1$ , ce qui donne comme nouvelle approximation de la racine $x 2 = x 1 + d 1 = 2,1$ . Il écrit ensuite $d 1 = 0,1 + d 2$ , où $d 2$ est donc l'accroissement à donner à $d 1$ pour obtenir la racine du polynôme précédent. Il remplace donc $d 1$ par $0,1 + d 2$ dans le polynôme précédent pour obtenir

$d_{2}^{3}+6{,}3\,d_{2}^{2}+11{,}23\,d_{2}+0{,}061=0$ .

On obtiendrait la même équation en remplaçant $x$ par $2,1 + d 2$ dans le polynôme initial. Négligeant les deux premiers termes, il reste $11,23 d 2 + 0,061 = 0$ ou $d 2 \approx -0,0054$ , ce qui donne comme nouvelle approximation de la racine $x 3 = x 2 + d 2 \approx 2,0946$ . On peut poursuivre les opérations aussi longtemps qu'il convient.

Cette méthode fut l'objet de publications antérieures. En 1685, John Wallis en publia une première description[3] dans A Treatise of Algebra both Historical and Practical. En 1690, Joseph Raphson en publia une description simplifiée dans Analysis aequationum universalis. Raphson considérait la méthode de Newton toujours comme une méthode purement algébrique et restreignait aussi son usage aux seuls polynômes. Toutefois, il mit en évidence le calcul récursif des approximations successives d'un zéro d'un polynôme au lieu de considérer comme Newton une suite de polynômes.

C'est Thomas Simpson (1710-1761) qui généralisa cette méthode au calcul itératif des solutions d'une équation non linéaire, en utilisant les dérivées (qu'il appelait fluxions, comme Newton)[4]. Simpson appliqua la méthode de Newton à des systèmes de deux équations non linéaires à deux inconnues[5], en suivant l'approche utilisée aujourd'hui pour des systèmes ayant plus de 2 équations, et à des problèmes d'optimisation sans contrainte en cherchant un zéro du gradient[6]. Arthur Cayley fut le premier à noter la difficulté de généraliser la méthode de Newton aux variables complexes en 1879[7], par exemple aux polynômes de degré supérieur à 3.

On pourra consulter l'article de Ypma (1995) pour d'autres informations sur l'historique de l'algorithme. Cet auteur attribue l'absence de reconnaissance aux autres contributeurs de l'algorithme au livre influent de Fourier, intitulé Analyse des Équations Déterminées (1831), lequel décrivait la méthode newtonienne sans faire référence à Raphson ou Simpson.

Fonction réelle d'une variable réelle

L'algorithme

On va donc chercher à construire une bonne approximation d'un zéro de la fonction d'une variable réelle $f (x)$ en considérant son développement de Taylor au premier ordre. Pour cela, partant d'un point $x 0$ que l'on choisit de préférence proche du zéro à trouver (en faisant des estimations grossières par exemple), on approche la fonction au premier ordre, autrement dit, on la considère asymptotiquement égale à sa tangente en ce point :

$f(x)\simeq f(x_{0})+f'(x_{0})(x-x_{0}).$

Partant de là, pour trouver un zéro de cette fonction d'approximation, il suffit de calculer l'intersection de la droite tangente avec l'axe des abscisses, c'est-à-dire résoudre l'équation affine :

$0=f(x_{0})+f'(x_{0})(x-x_{0}).$

On obtient alors un point $x 1$ qui en général a de bonnes chances d'être plus proche du vrai zéro de $f$ que le point $x 0$ précédent. Par cette opération, on peut donc espérer améliorer l'approximation par itérations successives (voir illustration) : on approche à nouveau la fonction par sa tangente en $x_{1}$ pour obtenir un nouveau point $x 2$ , etc.

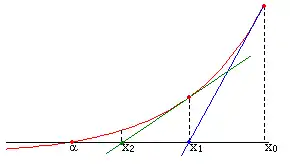
Illustration de la méthode de Newton.

Illustration animée de la méthode.

Cette méthode requiert que la fonction possède une tangente en chacun des points de la suite que l'on construit par itération, par exemple il suffit que $f$ soit dérivable.

Formellement, on part d'un point $x 0$ appartenant à l'ensemble de définition de la fonction et on construit par récurrence la suite :

$x_{k+1}=x_{k}-{\frac {f(x_{k})}{f'(x_{k})}},$

où $f'$ désigne la dérivée de la fonction $f$ . Le point $x k +1$ est bien la solution de l'équation affine $f(x_{k})+f'(x_{k})(x-x_{k})=0$ .

Il se peut que la récurrence doive se terminer, si à l'étape $k$ , $x k$ n'appartient pas au domaine de définition ou si la dérivée $f' (x k)$ est nulle ; dans ces cas, la méthode échoue.

Si le zéro inconnu $α$ est isolé, alors il existe un voisinage de $α$ tel que pour toutes les valeurs de départ $x 0$ dans ce voisinage, la suite $(x k)$ va converger vers $α$ . De plus, si $f' (α)$ est non nul, alors la convergence est (au moins) quadratique, ce qui signifie intuitivement que le nombre de chiffres corrects est approximativement doublé à chaque étape.

Bien que la méthode soit très efficace, certains aspects pratiques doivent être pris en compte. Avant tout, la méthode de Newton nécessite que la dérivée soit effectivement calculée. Dans les cas où la dérivée est seulement estimée en prenant la pente entre deux points de la fonction, la méthode prend le nom de méthode de la sécante, moins efficace (d'ordre 1,618 qui est le nombre d'or) et inférieure à d'autres algorithmes. Par ailleurs, si la valeur de départ est trop éloignée du vrai zéro, la méthode de Newton peut entrer en boucle infinie sans produire d'approximation améliorée. À cause de cela, toute mise en œuvre de la méthode de Newton doit inclure un code de contrôle du nombre d'itérations.

Exemple

Pour illustrer la méthode, recherchons le nombre positif $x$ vérifiant $cos(x) = x 3$ . Reformulons la question pour introduire une fonction devant s'annuler : on recherche le zéro positif (la racine) de $f (x) = cos(x) - x 3$ . La dérivation donne $f' (x) = -sin(x) - 3 x 2$ .

Comme $\cos(x)\leqslant 1$ pour tout $x$ et $x 3 >1$ pour $x >1$ , nous savons que notre zéro se situe entre 0 et 1. Nous essayons une valeur de départ de $x 0 = 0,5$ .

{\begin{matrix}x_{1}&=&x_{0}-{\frac {f(x_{0})}{f'(x_{0})}}&=&0,5-{\frac {\cos(0,5)-0,5^{3}}{-\sin(0,5)-3\times 0,5^{2}}}&\simeq &1,112\,141\,637\,1\\x_{2}&=&x_{1}-{\frac {f(x_{1})}{f'(x_{1})}}&&\vdots &\simeq &0,909\,672\,693\,736\\x_{3}&&\vdots &&\vdots &\simeq &0,866\,263\,818\,209\\x_{4}&&\vdots &&\vdots &\simeq &0,865\,477\,135\,298\\x_{5}&&\vdots &&\vdots &\simeq &0,865\,474\,033\,111\\x_{6}&&\vdots &&\vdots &\simeq &0,865\,474\,033\,101\\x_{7}&&\vdots &&\vdots &\simeq &0,865\,474\,033\,102\end{matrix}}

Les 7 premiers chiffres de cette valeur coïncident avec les 7 premiers chiffres du vrai zéro.

Convergence

La vitesse de convergence d'une suite $x n$ obtenue par la méthode de Newton peut être obtenue comme application de la formule de Taylor-Lagrange. Il s'agit d'évaluer une majoration de $log| x n - a |$ .

$f$ est une fonction définie au voisinage de $a$ et deux fois continûment différentiable. On suppose que $a$ se trouve être un zéro de $f$ qu'on essaie d'approcher par la méthode de Newton. On fait l'hypothèse que $a$ est un zéro d'ordre 1, autrement dit que $f' (a)$ est non nul. La formule de Taylor-Lagrange s'écrit :

0=f(a)=f(x)+f'(x)(a-x)+{\frac {f''(\xi )}{2}}{(a-x)^{2}}

, avec

ξ

entre

x

a

Partant de l'approximation $x$ , la méthode de Newton fournit au bout d'une itération :

N_{f}(x)-a=x-{\frac {f(x)}{f'(x)}}-a={\frac {f''(\xi )}{2\,f'(x)}}(x-a)^{2}

Pour un intervalle compact $I$ contenant $x$ et $a$ et inclus dans le domaine de définition de $f$ , on pose : $m 1 = min x \in I | f' (x) |$ ainsi que $M 2 = max x \in I | f '' (x)|$ . Alors, pour tout $x \in I$ :

\left|N_{f}(x)-a\right|\leqslant {\frac {M_{2}}{2m_{1}}}|x-a|^{2}

Par récurrence immédiate, il vient :

K\left|x_{n}-a\right|\leqslant (K|x_{0}-a|)^{2^{n}}

où $K = M 2 / 2 m 1$ . En passant au logarithme :

\log \left|x_{n}-a\right|\leqslant 2^{n}\log(K|x_{0}-a|)-\log(K)

La convergence de $x n$ vers $a$ est donc quadratique, à condition que $| x 0 - a | < 1/ K$ .

Exemples de non-convergence

Les tangentes à la courbe représentant la fonction

x\mapsto x^{3}-2x+2

en 0 et en 1 coupent l'axe des

x

en 1 et en 0 respectivement. Si l'on prend 0 ou 1 comme point de départ, la méthode oscille entre ces deux points et ne converge donc pas.

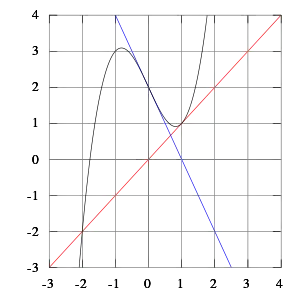
La tangente à la courbe peut couper l'axe des abscisses hors du domaine de définition de la fonction.

Si l'on utilise l'algorithme de Newton pour trouver l'unique zéro $x * = 0$ de la fonction $x\in \mathbb {R} \mapsto |x|^{1/2}$ en prenant un itéré initial $x 0 \neq 0$ , on constate que, pour tout $k\in \mathbb {N}$ , $x k +1 =- x k$ ; la suite générée ne converge donc pas, même localement (c'est-à-dire même si $x 0$ est pris proche du zéro $x * = 0$ ). Le problème provient ici, en particulier, de la non-différentiabilité de la fonction en l'unique zéro $x * = 0$ .

Critère d'arrêt

Des critères d'arrêt possibles, déterminés relativement à une grandeur numériquement négligeable, sont :

\|f(x_{k})\|<\varepsilon _{1}\qquad \mathrm {ou} \qquad \|x_{k+1}-x_{k}\|<\varepsilon _{2}

où $\varepsilon _{1},\varepsilon _{2}\in \mathbb {R} ^{+}$ représentent des erreurs d'approximations caractérisant la qualité de la solution numérique.

Dans tous les cas, il se peut que le critère d'arrêt soit vérifié en des points ne correspondant pas à des solutions de l'équation à résoudre.

Racine carrée

Un cas particulier de la méthode de Newton est la méthode de Héron, aussi appelée méthode babylonienne : il s'agit, pour calculer la racine carrée de $a$ , d'appliquer la méthode de Newton à la fonction $f$ définie par

f(x)=x^{2}-a

On obtient alors, en utilisant la formule de la dérivée $f' (x) = 2 x$ , une méthode d'approximation de la solution $\sqrt a$ donnée par la formule itérative suivante :

x_{k+1}:=x_{k}-{\frac {x_{k}^{2}-a}{2x_{k}}}={\frac {1}{2}}\left(x_{k}+{\frac {a}{x_{k}}}\right)

Pour tout $a \geq 0$ et tout point de départ $x 0 > 0$ , cette méthode converge vers $\sqrt a$ .

On peut l'étendre au calcul de toute racine $n$ -ième d'un nombre $a$ avec la formule :

x_{k+1}:=x_{k}-{\frac {x_{k}^{n}-a}{nx_{k}^{n-1}}}={\frac {1}{n}}\left({(n-1)x_{k}+{\frac {a}{x_{k}^{n-1}}}}\right)

Intersection de graphes

On peut déterminer une intersection des graphes de deux fonctions réelles dérivables $f$ et $g$ , c'est-à-dire un point $x$ tel que $f (x) = g (x)$ , en appliquant la méthode de Newton à la fonction $f - g$ .

Fonctions holomorphes

La méthode de Newton appliquée au polynôme

z 3 - 1

à variable complexe

z

converge à partir de tous les points du plan (des nombres complexes) colorés en rouge, vert ou bleu vers l'une des trois racines de ce polynôme, chacune des couleurs correspondant à une racine différente. Les points restants, se trouvant sur la structure plus claire — appelée fractale de Newton — sont les points de départ pour lesquels la méthode ne converge pas.

La méthode peut aussi être utilisée pour trouver des zéros de fonctions holomorphes. Dans ce cadre, on connaît bien les comportements que peut avoir la suite des itérés de Newton. On peut citer :

convergence vers un zéro ;
limite infinie ;
la suite admet un cycle limite autrement dit, la suite peut être découpée en $p$ sous-suites disjointes de la forme $(z n 0 + kp) k$ qui chacune convergent vers des points distincts (qui ne sont pas des zéros de $f$ ) formant un cycle périodique pour la fonction $z - f (z) / f' (z)$ ;
la suite se rapproche de l'ensemble des zéros de la fonction sans qu'il n'y ait toutefois de cycle limite, et à chaque étape de l'itération, on se retrouve proche d'un zéro différent des précédents ;
la suite a un comportement chaotique, etc.

L'ensemble des points à partir desquels peut être obtenue une suite qui converge vers un zéro fixé s'appelle le bassin d'attraction de ce zéro. Pour beaucoup de fonctions complexes, le bassin d'attraction est une fractale.

L'étude de la méthode de Newton pour les polynômes à variables complexes trouve naturellement sa place dans l'étude dynamique des fractions rationnelles et a été une des motivations récentes de l'étude de la dynamique holomorphe.

Généralisations/variantes

Systèmes d'équations à plusieurs variables

On peut aussi utiliser la méthode de Newton pour résoudre un système de $n$ équations (non linéaires) à $n$ inconnues $x = (x 1,..., x n)$ , ce qui revient à trouver un zéro d'une fonction $F$ de $\mathbb {R} ^{n}$ dans $\mathbb {R} ^{n}$ , qui devra être différentiable. Dans la formulation donnée ci-dessus, il faut multiplier par l'inverse de la matrice jacobienne $F' (x k)$ au lieu de diviser par $f' (x k)$ . Évidemment, pour économiser du temps de calcul, on ne calculera pas l'inverse de la jacobienne, mais on résoudra le système d'équations linéaires suivant

$F\,'(x_{k})(x_{k+1}-x_{k})=-F(x_{k})$

en l'inconnue $x k +1 - x k$ . Encore une fois, cette méthode ne fonctionne que pour une valeur initiale $x 0$ suffisamment proche d'un zéro de $F$ .

Méthode de Newton approchée

Il arrive parfois que la dérivée (ou la matrice jacobienne pour un système d'équations à plusieurs variables) de la fonction $f$ soit coûteuse à calculer. La dérivée peut alors être approchée au moyen de différences finies. Par exemple, en approchant la dérivée $f' (x k)$ par

{\frac {f(x_{k})-f(x_{k-1})}{x_{k}-x_{k-1}}},

on obtient la méthode de la sécante. La convergence de cette méthode n'est plus quadratique, mais reste sur-linéaire (en fait, d'ordre $φ = 1 + \sqrt 5 / 2 \approx 1,618$ ).

Méthode de Newton non lisse

Lorsque la fonction dont on cherche une racine est non-différentiable, mais seulement semi-lisse, la méthode de Newton ne génère pas nécessairement une suite ${x k}$ convergente, même si les itérés sont des points de différentiabilité de $f$ , arbitrairement proches d'un zéro de $F$ . Un contre-exemple est donné par Kummer (1988[8]).

Un algorithme analogue est encore possible en supposant un peu plus que la lipschitzianité de $F$ , mais sa semi-lissité. L'algorithme de Newton pour une fonction $f$ semi-lisse consiste alors à générer une suite $\{x_{k}\}\subset \mathbb {E}$ , où le nouvel itéré $x k +1$ est calculé à partir de l'itéré courant $x k$ par la récurrence suivante

x_{k+1}:=x_{k}-J_{k}^{-1}f(x_{k}),

où $J k$ est une jacobienne inversible du différentiel de Clarke $\partial CF (x k)$ , qui est supposée exister.

Comme la méthode de Newton classique, l'algorithme de Newton semi-lisse converge sous deux conditions. La première spécifie que la fonction dont on cherche un zéro $x *$ est suffisamment lisse : elle doit être semi-lisse. Il faut aussi qu'en ce zéro la fonction ait ses « pentes » qui ne s'annulent pas en $x *$ ; ceci s'exprime par l'hypothèse de C-régularité du zéro. Il s'agit aussi d'un résultat de convergence locale, ce qui veut dire qu'il faut que le premier itéré soit choisi suffisamment près d'un zéro satisfaisant les conditions ci-dessus pour que la convergence ait lieu.

Convergence locale de l'algorithme de Newton semi-lisse — Supposons que $f$ soit semi-lisse en une solution C-régulière $x *$ de l'équation $f (x) = 0$ . Alors,

il existe un voisinage $V$ de $x *$ tel que si le premier itéré $x 1 \in V$ , l'algorithme de Newton semi-lisse est bien défini et génère une suite ${x k}$ dans $V$ , qui converge super-linéairement vers $x *$ ,
la convergence est quadratique si $f$ est fortement semi-lisse en $x *$ .

Un état de l'art est donné par Izmailov et Solodov[9].

Méthode de Newton par intervalles

Dans certains cas, il arrive que l'on veuille éviter la condition de proximité entre notre valeur de départ et le zéro de la fonction. Une solution est alors d'utiliser la méthode de Newton par intervalles[10] - [11].

On considère $f\in {\mathcal {C}}^{1}(X)$ , avec $X$ un intervalle réel, et on suppose que l'on a une extension par intervalles $F'$ de $f '$ , c'est-à-dire une fonction $F '$ prenant en entrée un intervalle $Y \subseteq X$ et renvoyant un intervalle $F' (Y)$ tel que :

{\begin{aligned}F'([y,y])&=\{f'(y)\}\\F'(Y)&\supseteq \{f'(y)~|~y\in Y\}\end{aligned}}

On suppose également que $0\notin F'(X)$ , donc en particulier $f$ a au plus un zéro sur $X$ . On peut maintenant définir l'opérateur :

N(Y)=m+{\frac {f(m)}{F'(Y)}}=\left\{\left.m+{\frac {f(m)}{z}}~\right|~z\in F'(Y)\right\}

pour tout intervalle $y$ de centre $m$ . On notera que l'hypothèse sur $F'$ implique que $N (Y)$ est bien défini et est un intervalle (voir arithmétique d'intervalles pour plus de détails là dessus). On peut maintenant créer la suite d'intervalles suivante :

{\begin{aligned}X_{0}&=X\\X_{k+1}&=N(X_{k})\cap X_{k}\end{aligned}}

Le théorème des accroissements finis certifie que, s'il y a un zéro de $f$ dans $X k$ , alors il est encore dans $X k +1$ . De plus, l'hypothèse de positivité sur $F'$ implique que la taille de $X k +1$ est au plus la moitié de celle de $X k$ , donc la séquence converge vers le singleton ${x *}$ , où $x *$ est le zéro de $f$ sur $X$ .

Annexes

Notes

Joseph Louis Lagrange et Louis Poinsot, Traité de la résolution des équations numériques de tous les degrés.
Dans Methodus fluxionum et serierum infinitorum selon J.-L. Chabert et al. (1994). Ypma (1995) renvoie aux pages 219-220 du volume II chez Whiteside (1967-1976).
(en) Eric W. Weisstein, « Wallis's Constant », sur MathWorld.
Voir Simpson (1740), pages 83-84, selon Ypma (1995).
Voir Simpson (1740), page 82, selon Ypma (1995).
(en) T. Simpson (1737), A New Treatise of Fluxions.
(en) Arthur Cayley (1789). The Newton-Fourier imaginary problem.
(en) B. Kummer (1988). Newton’s method for nondifferentiable functions. In (en) J. Guddat, B. Bank, H. Hollatz, P. Kall, D. Klatte, B. Kummer, K. Lommatzsch, L. Tammer, M. Vlach et K. Zimmerman, Advances in Mathematical Optimization, Berlin, Akademie-Verlag, 114–125 p..
(en) A. F. Izmailov et M. V. Solodov, « Newton-Type Methods for Optimization and Variational Problems », Springer Series in Operations Research and Financial Engineering, Springer,‎ 2014.
(en) RE Moore, Methods and applications of interval analysis, vol. 2, Siam, 1979
(en) E. Hansen, « Interval forms of Newtons method », Computing, vol. 2, n^o 20,‎ 1978, p. 153-163

Liens externes

J. Ch. Gilbert, Éléments d'Optimisation Différentiable — Théorie et Algorithmes, syllabus de cours à l'ENSTA ParisTech, Paris.
N. Soualem (2006). Méthode de Newton sur math-linux.com.

Références

(en) D. P. Bertsekas (1995), Nonlinear Programming. Athena Scientific. (ISBN 978-1-886529-14-4).
(en) J. F. Bonnans, J. Ch. Gilbert, C. Lemaréchal, C. Sagastizábal (2006), Numerical Optimization - Theoretical and Practical Aspects [détail des éditions].
J.-L. Chabert, É. Barbin, M. Guillemot, A. Michel-Pajus, J. Borowczyk, A. Djebbar, J.-C. Martzloff (1994). Histoire d’Algorithmes – Du Caillou à la Puce. Regards sur la Science. Belin, Paris.
J.-P. Dedieu (2006). Points Fixes, Zéros et la Méthode de Newton. Mathématiques et Applications 54. Springer Verlag, Berlin.
(en) P. Deuflhard (2004). Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms. Springer Series in Computational Mathematics, Vol. 35. Springer, Berlin, (ISBN 3-540-21099-7).
(en) A. F. Izmailov, M. V. Solodov (2014). Newton-Type Methods for Optimization and Variational Problems. Springer Series in Operations Research and Financial Engineering. Springer.
(en) J. Nocedal, S. J. Wright (2006), Numerical Optimization, Springer. (ISBN 978-0-387-30303-1).
(en) J. M. Ortega, W. C. Rheinboldt (2000). Iterative Solution of Nonlinear Equations in Several Variables. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics. (ISBN 0-89871-461-3).
(en) T. Simpson (1740). Essays on Several Curious and Useful Subjects in Speculative and Mix'd Mathematicks, Illustrated by a Variety of Examples. Londres.
(en) D. T. Whiteside, éditeur (1967-1976) The Mathematical Papers of Isaac Newton, Volumes I-VII, Cambridge University Press, Cambridge.
(en) T. J. Ypma (1995). Historical development of the Newton-Raphson method. SIAM Review, 37, 531–551.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.