Algorithme de Jaumain

On note (F , t) le flux financier F échéant à la date t. On appelle échéance moyenne des flux (F₁ , t₁), ..., (F_n , t_n) avec F_k ≥ 0 la date τ telle que :

${\displaystyle (F_{1},t_{1})+...+(F_{n},t_{n})=(F,\tau )}$ où ${\displaystyle F=F_{1}+...+F_{n}}$

La valeur τ est par exemple la date à laquelle un débiteur pourrait s’acquitter des dettes F₁, ..., F_n échéant respectivement aux dates t₁, ..., t_n par un paiement unique F égal à la somme arithmétique des dettes.

En égalant les valeurs actuelles, on obtient :

${\displaystyle Fv^{\tau }=\sum _{k=1}^{n}F_{k}v^{t_{k}}=F_{1}v^{t_{1}}+...+F_{n}v^{t_{n}}}$

d'où : ${\displaystyle \tau ={\frac {1}{\ln v}}\ln \left({\frac {F_{1}v^{t_{1}}+...+F_{n}v^{t_{n}}}{F}}\right)={\frac {\ln \left(F_{1}v^{t_{1}}+...+F_{n}v^{t_{n}}\right)-\ln F}{\ln v}}}$

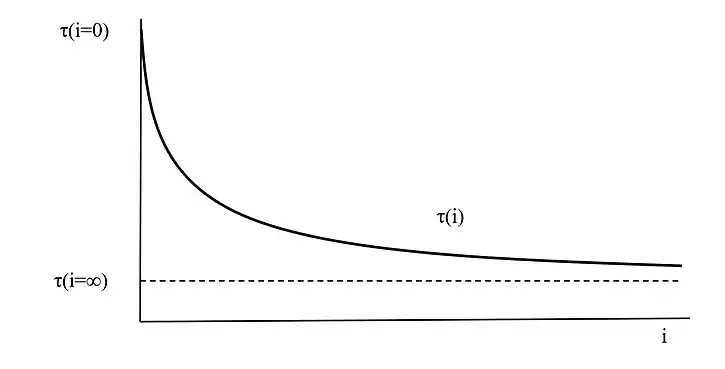
L’échéance moyenne dépend du taux d’actualisation adopté pour le calcul des valeurs actuelles. De manière plus précise, on note τ(i) l’échéance moyenne au taux d’actualisation i des flux (F₁, t₁), ..., (F_n, t_n).

Pour i=0, c’est-à-dire pour v = 1, la fonction τ(i) prend la forme indéterminée 0/0. En appliquant le théorème de l'Hospital, on obtient la vraie valeur :

${\displaystyle \tau (i=0)={\frac {F_{1}t_{1}+...+F_{n}t_{n}}{F}}}$

La valeur τ(i = 0) est donc l’échéance moyenne à intérêt simple des flux (F₁ , t₁), ..., (F_n , t_n). C’est le barycentre des points t₁, ... t_n de masse respective F₁, …, F_n c’est-à-dire la moyenne pondérée des échéances des flux.

Ce résultat fournit une interprétation financière remarquable du concept mathématique de vraie valeur.

Si i=0, l’égalité ${\displaystyle Fv^{\tau }=F_{1}v^{t_{1}}+...+F_{n}v^{t_{n}}}$ est vérifiée quel que soit τ : l’emprunteur peut s’acquitter à n’importe quelle date des dettes F₁, ..., F_n par le paiement unique F = F₁ + ... + F_n. Dans ce cas on peut donc, du point de vue financier, assigner à τ n’importe quelle valeur. La vraie valeur est, parmi cette infinité de valeurs qui toutes conviennent financièrement, la seule qui rende la fonction τ(i) continue quand i=0.

On démontre par ailleurs que τ est compris entre le plus petit et le plus grand des t_k et que, lorsque i→∞, τ tend vers le plus petit des t_k.

Pour i = ∞, c’est-à-dire pour v=0, la fonction τ(i) prend la forme indéterminée ∞/∞. En appliquant le théorème de l'Hospital, on obtient la vraie valeur :

${\displaystyle \tau (\infty )=t_{1}}$

On démontre enfin que la dérivée de τ(v) par rapport à v est nulle pour v=1 c’est-à-dire pour i=0 et est positive pour v<1, de sorte que τ est une fonction croissante de v<1 donc décroissante de i>0.

La dérivée de τ(v) vaut :

${\displaystyle \tau '(v)={\frac {-1}{v\ln ^{2}v}}{\frac {\sum _{k}F_{k}v^{t_{k}}}{\sum _{k}F_{k}}}+{\frac {1}{\ln v}}{\frac {\sum _{k}F_{k}t_{k}v^{t_{k}-1}}{\sum _{k}F_{k}v^{t_{k}}}}={\frac {1}{v\ln ^{2}v}}\left(\ln v{\frac {\sum _{k}F_{k}t_{k}v^{t_{k}}}{\sum _{k}F_{k}v^{t_{k}}}}-{\frac {\sum _{k}F_{k}v^{t_{k}}}{\sum _{k}F_{k}}}\right)}$

est du signe de

${\displaystyle z(v)={\frac {\sum _{k}F_{k}t_{k}v^{t_{k}}}{\sum _{k}F_{k}v^{t_{k}}}}\ln v-{\frac {\sum _{k}F_{k}v^{t_{k}}}{\sum _{k}F_{k}}}}$

qui est nul pour v = 1. La dérivée de z(v) est du signe de

${\displaystyle \left(\sum _{k}F_{k}t_{k}v^{t_{k}}\right)\left(\sum _{k}F_{k}t_{k}v^{t_{k}-1}\right)-\left(\sum _{k}F_{k}t_{k}^{2}v^{t_{k}-1}\right)\left(\sum _{k}F_{k}v^{t_{k}}\right)}$

Or, on démontre que :

${\displaystyle \left(\sum _{k=0}^{n-1}A_{k}\right)\left(\sum _{k=0}^{n-1}A_{k}B_{k}C_{k}\right)-\left(\sum _{k=0}^{n-1}A_{k}B_{k}\right)\left(\sum _{k=0}^{n-1}A_{k}C_{k}\right)=\sum _{h=0}^{n-2}\sum _{l=1,l>h}^{n-1}A_{h}A_{l}(B_{h}-B_{l})(C_{h}-C_{l})}$

Si ${\displaystyle A_{k}=F_{k}v^{t_{k}},\ B_{k}=t_{k},\ C_{k}=t_{k}/v}$, on voit que z’(v) est du signe de :

${\displaystyle -\sum _{h=1}^{n-1}\sum _{l=2,l>h}^{n}F_{h}F_{l}v^{t_{h}+t_{l}-1}(t_{h}-t_{l})^{2}}$

qui est négatif puisque les F_k sont positifs. z(v) est donc une fonction décroissante de v. Or z(1) = 0. Par conséquent z(v) > 0 pour v < 1.

La dérivée de τ(v) par rapport à v est donc bien positive pour v < 1, c'est-à-dire pour i > 0, de sorte que τ est une fonction croissante de v < 1 donc décroissante de i > 0.

Etude de l’échéance moyenne en fonction du taux d’actualisation

Cet algorithme a été proposé par Christian Jaumain[1] - [2] - [3] - [4] - [5] - [6]. La méthode a été reprise dans H.U. Gerber[7].

Soit les deux séries de flux financiers (C₁, r₁) + ... + (C_n, r_n) et (D₁, s₁) + ...+ (D_n, s_n), telles que :

${\displaystyle \sum _{k=1}^{n}(C_{k},r_{k})=\sum _{k=1}^{n}(D_{k},s_{k})}$

Cette relation signifie qu’il revient au même de posséder – ou d’être redevable – des capitaux C₁, …, C_n aux dates respectives r₁, ..., r_n et de posséder – ou d’être redevable – des capitaux D₁, …, D_n aux dates respectives s₁, ..., s_n.

Ainsi par exemple, si i est l’intérêt annuel payable à terme échu d’un capital unitaire :

(1 ; 0) = (i ; 1) + (i ; 2) + … + (i ; n–1) + (1+i ; n)

Sans nuire à la généralité on peut, quel que soit k, supposer :

1. les C_k et D_k sont positifs, quitte à transposer des termes de l’égalité d’un membre dans l’autre.
2. le nombre des C_k égal à celui des D_k, certains d’entre eux pouvant être nuls.

L’équilibre financier entre les deux séries (C₁ , r₁) + ... + (C_n , r_n) et (D₁ , s₁) + ... + (D_n , s_n) est réalisé pour zéro, un ou plusieurs taux d’actualisation particuliers qui sont les TRI.

On démontre qu’il existe un TRI unique positif si :

1. il n’y a qu’un seul changement de signe dans la séquence des flux (TRI unique) ;
2. la somme arithmétique des flux précédant le changement de signe est inférieure en valeur absolue à la somme arithmétique des flux suivants (TRI positif).

La méthode qui suit permet de calculer le TRI s’il est unique, ou un des TRI s’ils sont multiples.

Au taux d’actualisation i=0, soit respectivement ρ₀ et σ₀ l’échéance moyenne des flux (C₁, r₁), ..., (C_n, r_n) et (D₁, s₁), ..., (D_n, s_n) :

${\displaystyle \rho _{0}={\frac {\sum _{k=1}^{n}C_{k}r_{k}}{\sum _{k=1}^{n}C_{k}}}\ ,\ \sigma _{0}={\frac {\sum _{k=1}^{n}D_{k}s_{k}}{\sum _{k=1}^{n}D_{k}}}}$

L’équation à résoudre devient : (C , ρ₀) = (D , σ₀).

Le taux d’actualisation résultant de cette équation est :

${\displaystyle i_{0}=\left[{\frac {D}{C}}\right]^{1/(\sigma _{0}-\rho _{0})}-1}$

Au taux d’actualisation i=i₀, soit respectivement ρ₁ et σ₁ l’échéance moyenne des flux (C₁ , r₁), ..., (C_n , r_n) et (D₁ , s₁), ..., (D_n , s_n) :

${\displaystyle \rho _{1}={\frac {1}{\ln v_{0}}}\ln {\frac {C_{1}v_{0}^{r_{1}}+...+C_{n}v_{0}^{r_{n}}}{C}}}$

${\displaystyle \sigma _{1}={\frac {1}{\ln v_{0}}}\ln {\frac {D_{1}v_{0}^{s_{1}}+...+D_{n}v_{0}^{s_{n}}}{D}}}$

L’équation à résoudre devient : (C , ρ₁) = (D , σ₁).

Le taux d’actualisation résultant de cette équation est :

${\displaystyle i_{1}=\left[{\frac {D}{C}}\right]^{1/(\sigma _{1}-\rho _{1})}-1}$

et ainsi de suite. Si la suite {i₀, i₁, … } converge, alors la limite est solution de l’équation à résoudre, donc un TRI.

Remarque. Le premier itéré de l’algorithme de Jaumain fournit une valeur de départ qui peut s’avérer très utile aux autres méthodes.

On reprend l'exemple d'application de l'algorithme de Newton-Raphson :

On a : C = 1 + 5 + 4,5 = 10,5 et D = 5,5 + 7 = 12,5

Le calcul du premier itéré donne :

${\displaystyle \rho _{0}={\frac {1\times 0+5\times 1+4,5\times 2}{10,5}}=1,333333}$

${\displaystyle \sigma _{0}={\frac {5,5\times 3+7\times 4}{12,5}}=3,560000}$

d’où : i₀ = (12,5/10,5)^{1/(3,560000-1,333333)} – 1 = 8,144966%

Calcul du 2^e itéré :

ρ₁ = 1,317059

σ₁ = 3,550325

d’où : i₁ = (12,5/10,5)^{1/(3,550325-1,317059)} – 1 = 8,111995%

et ainsi de suite. Le tableau suivant résume le calcul des itérés successifs :

L’algorithme converge vers le TRI de 8,12002%, atteint dès la 3^e ligne.

Remarques

1. Les suites des échéances moyennes convergent également. L’itération peut être arrêtée lorsque l’écart entre deux échéances moyennes successives est suffisamment petite, par exemple 1/1000^e d’année.
2. Le premier itéré de l’algorithme des échéances moyennes fournit une excellente valeur de départ pour les autres méthodes. Ainsi, en adoptant i₀ = 8,144966% dans l’algorithme de Newton-Raphson, on obtient le tableau suivant :

Le TRI de 8,12002% est atteint dès la 3^e ligne.

Exemple 2

Le TRI est unique. On obtient le tableau des itérés successifs suivant :

Exemple 3

A priori, il y a 3 ou 1 TRI. Un rapide examen graphique permet de conclure qu’il n’existe qu’un seul TRI. On obtient le tableau des itérés successifs suivant :

La réglementation européenne (Directive européenne du 22 février 1990) prévoit l’introduction d’un taux annualisé effectif global (TAEG) qui doit, en principe, servir d’instrument de comparaison pour toutes les formes de crédit à la consommation dans tous les Etats membres. Cette directive a été transposée dans la législation belge (loi du 6 juillet 1992, arrêté royal du 4 août 1992, M.B. 08.09.1992). En annexe à l’arrêté royal précité figure une méthode de calcul reprenant, sans en citer la source, l’algorithme des échéances moyennes tel que présenté ci-avant. Un communiqué du Moniteur Belge du 28.09.1993 précise que « La méthode de calcul donnée à l’annexe 1 de l’arrêté royal est due au professeur Christian Jaumain, de l’Université catholique de Louvain. Elle est décrite dans le Bulletin de l’Association des Actuaires suisses, Vol.79 – n°2, 1979 ».

Contrairement à ce que pourrait laisser supposer son appellation, le TRI ne reflète pas nécessairement le rendement effectif. L’appellation « taux actuariel » est sans doute préférable, car elle rend mieux compte du caractère ambigu de ce taux.