Équation cubique
En mathématiques, une équation cubique est une équation polynomiale de degré 3, de la forme ax3 + bx2 + cx + d = 0 avec a non nul, où les coefficients a, b, c et d sont en général supposés réels ou complexes.
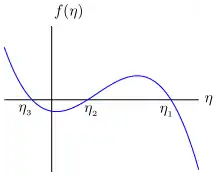
Historique
Antiquité
Les équations cubiques étaient connues des anciens Babyloniens, Grecs, Chinois, Indiens et Égyptiens[1] - [2] - [3].
On a trouvé des tablettes babyloniennes (XXe au XVIe siècle av. J.-C.) avec, en écriture cunéiforme, des tables de calcul de cubes et de racines cubiques[4] - [5]. Les Babyloniens auraient pu utiliser ces tables pour résoudre des équations cubiques, mais on n'en a aucune preuve[6].
Le plus simple et le plus ancien des problèmes du 3e degré, le problème de la duplication du cube, était considéré par les anciens Égyptiens comme insoluble[7]. Au Ve siècle av. J.-C., Hippocrate réduisit ce problème à celui de trouver deux proportions entre une longueur donnée et son double (a/x = x/y = y/(2a)), mais il ne pouvait pas les construire à la règle et au compas[8], tâche dont on sait maintenant qu'elle est impossible.
On suppose qu'Hippocrate, Ménechme (vers 380 à 320 av. J.-C.) et Archimède (Syracuse, 287 à 212 av. J.-C.) sont arrivés près de résoudre géométriquement le problème de la duplication du cube par intersection de coniques[8] : Ménechme, pour obtenir x tel que x3 = a2b, se ramène à l'intersection de x2 = ay (parabole) et de xy = ab (hyperbole). Si des historiens des mathématiques comme Reviel Netz mettent en doute le fait que les Grecs pensaient aux équations cubiques comme telles, et pas seulement à des problèmes qui peuvent y conduire, quelques autres, comme Thomas Heath (qui a traduit les œuvres d'Archimède) sont en désaccord, avançant qu'Archimède a non seulement résolu des équations cubiques par intersection de deux coniques, mais a même discuté des conditions pour que les solutions soient au nombre de 0, 1 ou 2[9]. Archimède avait cherché à couper une sphère de rayon r par un plan de façon que le rapport des volumes des deux parties ait une valeur donnée k. Cela donne une équation du 3e degré : si h est la hauteur d'une des parties, alors h3 + (4kr3)/(k + 1) = 3rh2.
Au IIIe siècle, le mathématicien grec Diophante trouve des solutions réelles ou rationnelles pour certaines équations cubiques à deux variables (équations diophantiennes)[3] - [10].
Moyen Âge
Des méthodes de résolution d'équations cubiques apparaissent dans Les Neuf Chapitres sur l'art mathématique, un texte mathématique chinois écrit autour du IIe siècle av. J.-C. et commenté par Liu Hui au IIIe siècle[2]. Au VIIe siècle (sous la dynastie Tang), l'astronome et mathématicien Wang Xiaotong, dans son traité mathématique intitulé Jigu Suanjing, pose systématiquement et résout numériquement 25 équations cubiques de la forme x3 + px2 + qx = N, dont 23 avec p, q ≠ 0 et 2 avec q = 0[11].
Au XIe siècle, le poète-mathématicien Omar Khayyam (1048-1131), originaire de Perse, fait des progrès significatifs dans la théorie des équations cubiques. Il découvre qu'une équation cubique peut avoir plus d'une solution et déclare qu'elle ne peut pas être résolue à la règle et au compas. Il trouve aussi une solution géométrique (voir infra)[12] - [13]. Il est le premier, dans son traité ultérieur Démonstrations de problèmes d'algèbre (vers 1070), à classifier complètement les équations cubiques, par intersection de coniques, donnant le nombre des racines réelles et des solutions géométriques générales[14] - [15].
Un siècle plus tard, le mathématicien indien Bhaskara II essaye de résoudre des équations cubiques, sans succès. Cependant, il donne un exemple d'une équation cubique : x3 + 12x = 6x2 + 35[16].
Au XIIe siècle encore, un autre mathématicien persan, Sharaf al-Dīn al-Tūsī (1135-1213), écrit le Al-Mu'ādalāt (Traité sur les équations), où il classe les équations cubiques suivant l'existence de racines strictement positives, et non pas, comme Omar Khayyam, suivant le signe des coefficients. Son étude porte sur huit types d'équations cubiques avec des solutions positives, et cinq types d'équations cubiques qui peuvent ne pas avoir de solutions positives. Il inaugure à cet effet l'étude des fonctions polynomiales, introduisant leur dérivée, recherchant leurs extrema, etc.[17]. Il comprend l'importance du discriminant pour trouver des solutions algébriques à certains types d'équations cubiques[18]. Il utilise aussi ce qui sera connu plus tard comme la « méthode de Ruffini-Horner » pour approcher numériquement la solution d'une équation cubique. Il résout les problèmes liés à l'homogénéité de dimension : le nombre x s'identifie aussi bien à une longueur qu'à une aire rectangulaire de côtés 1 et x ou encore à un volume (1, 1, x).
Leonardo Fibonacci a donné, dans son ouvrage Flos (1225), une valeur approchée extrêmement précise (à 10–9 près) de la solution positive de l'équation cubique x3 + 2x2 + 10x = 20 : en base 60, il a donné le résultat 1, 22, 7, 42, 33, 4, 40, qui signifie : 1 + 22/60 + 7/602 + 42/603 + 33/604 + 4/605 + 40/606[19].
Scipione del Ferro
En 1494, Luca Pacioli écrit un important traité : Summa de arithmetica, geometria, de proportioni et de proportionalita. Il y fait la somme des connaissances en mathématiques (plus particulièrement en algèbre) transmise par les Arabes. On trouve dans ce traité la résolution complète des équations des premier et deuxième degrés sans les solutions négatives. Concernant les équations de degré trois, il reconnait que celles-ci semblent non résolubles par des méthodes algébriques, compte tenu des connaissances mathématiques atteintes[20].
Scipione del Ferro est enseignant à l'université de Bologne de 1496 à 1526[21]. Il est possible qu'il y ait rencontré Luca Pacioli qui y enseignait entre 1501 à 1502[22]. La suite de l'histoire ne nous est connue que par les témoignages de son gendre, Annibal de la Nave (ou Hannival Nave), marié à sa fille, Filippa, et d'un de ses élèves Antonio Maria del Fiore[23]. Vers les années 1510-1515, del Ferro aurait découvert une méthode fournissant une solution, sous forme de radicaux, de la racine réelle de l’équation du troisième degré sans terme quadratique (coefficient de x2 nul). La découverte de cette formule est un immense pas en avant dans l’histoire des équations. Les travaux de del Ferro portent essentiellement sur la résolution des équations de la forme x3 = px + q, x3 + px = q ou x3 + q = px, où p et q sont des entiers naturels (on ne travaillait autrefois qu’avec des nombres positifs, les nombres négatifs paraissent encore étranges et d'un maniement délicat), formes aujourd’hui unifiées et généralisées par x3 + px + q = 0 où p et q sont des entiers relatifs.
Il consigne ses travaux dans des notes personnelles et dans un cahier. En raison de sa réticence (courante à l’époque), il ne publie pas son œuvre, et ne veut communiquer ses travaux qu’à un groupe très réduit de personnes, quelques amis et élèves.
À sa mort en 1526, son gendre, Annibal de la Nave, également mathématicien, qui lui succède à l'université de Bologne[24], aurait hérité de ses notes, et donc de toutes ses découvertes inscrites dans ce fameux cahier. Selon Morris Kline, del Ferro aurait confié sa méthode à la fois à Fiore et à de la Nave[25]. Toutefois, ses notes ont depuis définitivement disparu, et il ne reste aucune trace directe de ses travaux.
Niccolò Fontana Tartaglia

Le reste des évènements est raconté par Tartaglia et Cardan.
En 1530, Niccolò Fontana Tartaglia reçoit deux problèmes d'équations cubiques de Zuanne da Coi[26]. Da Coi est connu pour proposer des problèmes dont lui-même ne connait pas la solution. Une des équations est de la forme x3 + mx2 = n et Tartaglia lui répond qu'il est convaincu de connaitre une méthode générale de résolution pour ce type d'équation[27]. Il est aussitôt contesté par Fiore, ce qui les conduit à un célèbre concours, en 1535. Chaque participant doit proposer trente problèmes dont il connait la résolution à son rival, le gagnant doit offrir 30 banquets au perdant[28].
Fiore propose des questions se réduisant à des équations de la forme x3 + mx = n, pour lesquelles il connait une méthode générale de résolution. Les questions de Tartaglia sont plus diverses et certaines d'entre elles conduisent à des équations de la forme x3 + mx2 = n[29]. Selon Tartaglia, il ne connaissait alors pas de méthode de résolution pour les équations de Fiore et ce n'est que 8 jours avant la date limite du concours qu'il aurait trouvé la méthode générale et aurait résolu en quelques heures les trente équations proposées par son concurrent alors que ce dernier n'aurait pas pu résoudre toutes les siennes[28].
Beau joueur, il renonce à réclamer le prix des trente banquets. Il conserve secrète sa méthode de résolution, à l’instar de Scipione del Ferro.
Jérôme Cardan
En tant que conférencier de mathématique à Milan, Jérôme Cardan connaissait le problème de la résolution du 3e degré. Il était d'accord avec la Summa de Luca Pacioli qui déclarait que la résolution algébrique des équations du 3e degré était impossible. Il est donc très intrigué après le défi entre Fiore et Tartaglia. En 1539, il contacte Tartaglia et lui demande de lui confier sa méthode en lui promettant de garder le secret. Ce dernier refuse. Cardan lui propose de le présenter au Marquis d'Avalos, gouverneur de Milan, qui pourrait apporter à Tartaglia protection et soutien[30] . Tartaglia révise alors sa position, réalisant que l'appui du gouvernement milanais pouvait être une aide non négligeable à son ascension sociale. Il accepte de se rendre à Milan et finit par céder aux arguments de Cardan. Il consent à lui révéler sa méthode de résolution des équations incomplètes, à condition que ce dernier jure de ne jamais la divulguer. Il la lui confie sous la forme cryptée d'un poème que Cardan met quelque temps à comprendre.
En 1542, Cardan et Ludovico Ferrari se rendent à Bologne et apprennent d'Annibal de la Nave que Scipione del Ferro avait résolu bien avant Tartaglia les équations du 3e degré. Pour le leur prouver, il leur aurait montré le cahier du feu Del Ferro[31] . Bien qu'il ait juré de ne jamais révéler la méthode de Tartaglia, Cardan pense que rien ne l'empêche de publier celle de Del Ferro.
En 1545, Cardan publie Ars Magna (Le Grand Art). Il y expose la méthode de résolution de Tartaglia en lui en attribuant bien la paternité. Il complète son exposé par une justification de la méthode et l'étend à l'ensemble de tous les autres cas. Il publie, à cette occasion, la méthode de résolution de l'équation du 4e degré mis au point par son élève Ludovico Ferrari. L'importance de l’œuvre de Cardan fait que la postérité ne retiendra que son nom et que cette méthode de résolution va porter le nom de méthode de Cardan.
Tartaglia est furieux quand il découvre que Cardan a transgressé sa promesse. Il publie, en 1546, un livre Quesiti et inventioni diverse (Quelques problèmes et inventions) dans lequel il révèle sa version de l'histoire et sans cacher le parjure de Cardan. Furieux, il y insulte violemment Cardan qui est défendu par Ferrari. S'ensuivent une série de défis et de réponses entre Ferrari et Tartaglia qui les conduisent à un débat public en 1548, dans une église à Milan devant quelques personnalités. Sur l'issue de ce débat, les récits diffèrent : d'après Cardan, Ferrari aurait fait une meilleure prestation que Tartaglia, tandis que Tartaglia accuse Ferrari d'avoir réuni un public acquis à sa cause qui l'aurait empêché de développer ses idées[31]. Tartaglia déclare alors forfait et quitte Milan.
Il reste cependant un cas qui pose problème à Cardan : le cas où la résolution de l'équation du second degré auxiliaire conduit à un discriminant négatif. C'est ce qu'on appelle le cas irréductible. L'équation admet pourtant des solutions réelles. Dans les échanges entre Tartaglia et Cardan entre 1539 et 1542, Cardan évoque ce problème et reçoit de Tartaglia une réponse élusive : il y aurait alors « d'autre façons » de résoudre l'équation[32]. Dans son Ars Magna, Cardan présente bien un cas de résolution d'équation du second degré avec discriminant négatif utilisant des quantités non réelles sorties de son imagination. Mais il n'exploite pas cette idée pour la résolution de l'équation du troisième degré[33]. Il faut attendre Bombelli et la mise en place des nombres complexes pour que ce sujet soit abordé.
Raphaël Bombelli
Après qu'en 1546, la controverse entre Cardan et Tartaglia devint publique avec la parution des Quesiti et inventioni diverse de Tartaglia, Raphaël Bombelli, admirateur de Cardan, conçut le projet d'écrire un traité d'algèbre : Algebra. Celui-ci, exposition systématique et logique des connaissances algébriques de l'époque, est rédigé entre 1557 et 1560, et reprend les travaux de Cardan de son vivant. Cette œuvre ne sera publiée que quelques mois avant la mort de son auteur.
En ce qui concerne les équations de degré supérieur à 2, Bombelli comme ses contemporains, traite un grand nombre de cas, ne considérant que les coefficients positifs, mais son habileté et sa maîtrise à utiliser formellement les racines de nombres négatifs le rendent capable d'établir que la formule de Scipione del Ferro est valable dans tous les cas. On peut dire que la solution du cas irréductible de l'équation cubique lui revient. L'équation du 4e degré est aussi traitée par la méthode de Ferrari.
En étudiant les formules de Cardan, il est amené à introduire son fameux piu di meno. Les nombres imaginaires sont nés. Il remarqua que lorsque la formule de Cardan aboutissait à un discriminant négatif, la méthode géométrique donnait une solution réelle positive. Il sera le premier à utiliser dans ses calculs, à titre transitoire, des racines carrées imaginaires de nombres négatifs pour obtenir finalement la solution réelle tant recherchée. Il arriva à la conclusion que toute équation du 3e degré possédait au moins une solution réelle.
Il appelle les racines carrées d'une quantité négative, piu di meno et meno di meno. Bombelli considère les racines des équations comme des sommes algébriques de nombres positifs affectés d'un des quatre signes suivants : piu, meno, piu di meno, meno di meno, qui correspondent à peu près aux signes modernes +, –, +i, –i.
Successeurs
François Viète (1540-1603) a dérivé la solution trigonométrique pour des équations cubiques avec trois racines réelles, et René Descartes (1596-1650) a étendu le travail de Viète[34].
C'est Leonhard Euler (1707-1783)[35] qui aura éclairci la détermination des trois racines d’une équation cubique[36].
Résolution
On considère une équation cubique, de la forme ax3 + bx2 + cx + d = 0, avec . En posant x = z - b3a, on se ramène à une équation de la forme z3 + pz + q = 0 (cette technique se généralise à tout degré)[37].
Discriminant
L'équation a une racine multiple si et seulement si son discriminant[38],
- ,
est nul (sous la forme réduite z3 + pz + q = 0, ce discriminant vaut -4p3 - 27q2).
De plus, dans le cas d'une équation à coefficients réels, le nombre de racines réelles est déterminé par le signe du discriminant[39] :
- si Δ > 0, alors l'équation admet trois racines réelles distinctes ;
- si Δ = 0, alors l'équation admet une racine double ou triple et toutes ses racines sont réelles ;
- si Δ < 0, alors l'équation admet trois racines distinctes, dont une réelle et deux complexes conjuguées.
Méthode de Cardan
La méthode de del Ferro et Tartaglia, publiée par Cardan (voir supra), est exposée dans :
Substitution de Viète
La méthode de Viète pour résoudre
- ,
plus simple que celle de Cardan mais aboutissant aux mêmes formules, consiste (si p ≠ 0) à poser
- .
On obtient alors une équation du second degré sur Y = y3 :
de discriminant égal à ; c'est donc précisément lorsque cette équation n'a pas de racines réelles que l'équation originale en possède trois.
Pour plus de détails :
Méthode de Lagrange
La méthode de Lagrange pour les équations cubiques aboutit aux mêmes formules que celle de Cardan, mais par des idées qui « peuvent être considérées comme les prémices de la théorie de Galois » et dans lesquelles « Galois trouva d'ailleurs certainement son inspiration » ; elles permirent à Lagrange de résoudre aussi les équations de degré 4, et de « pressent[ir] que les équations de degré supérieur ne sont pas résolubles en général et développe[r] même quelques arguments en faveur de cette hypothèse »[40].
Les étapes pour résoudre ax3 + bx2 + cx + d = 0 sont de :
- numéroter arbitrairement les solutions ;
- poser ;
- « remarquer » que sont des polynômes symétriques en ;
- les exprimer en fonction de ;
- calculer alors , en résolvant l'équation du second degré dont sont solutions ;
- en déduire les valeurs de et de .
Pour plus de détails :
Autres méthodes
- Méthode de Tschirnhaus
- Méthode de Bézout
- Certaines équations cubiques peuvent être résolues par la trigonométrie[41] - [42], circulaire[43] ou hyperbolique.
Les coefficients ne sont pas nécessairement des nombres complexes. Une grande partie des méthodes de résolution est valable pour des coefficients dans n'importe quel corps de caractéristique nulle ou strictement supérieure à 3. Les solutions de l'équation cubique n'appartiennent pas nécessairement au même domaine que celui des coefficients. Par exemple, certaines équations cubiques à coefficients rationnels ont des racines complexes non rationnelles (voire non réelles).
Expression générale des solutions
La solution générale de l'équation cubique nécessite de calculer d'abord :
- ,
- .
Si le discriminant Δ a déjà été calculé, alors l'égalité Δ12 − 4Δ03 = −27 a2Δ peut être utilisée pour simplifier le calcul de C.
Il existe trois racines cubiques possibles impliquées par l'expression, dont au moins deux sont des nombres complexes non réels ; n'importe lequel d'eux peut être choisi lors de la définition C. La formule générale pour l'une des racines, en fonction des coefficients, est la suivante :
- .
Il faut noter que, bien que cette égalité est valable pour tout C différent de zéro, elle n'est pas la forme la plus pratique pour les racines multiples (Δ = 0), qui est traité dans la section suivante. Le cas où C = 0 ne se produit que lorsque Δ et Δ0 sont nuls et est également traité dans la section suivante.
Les deux autres racines de l'équation cubique peuvent être déterminées en utilisant la même égalité, en utilisant les deux autres choix pour la racine cubique dans l'équation pour C : désignant le premier choix C, les deux autres sont jC et jC, où j = (−1 + i√3)/2 (qui est une racine cubique de l'unité).
L'égalité ci-dessus peut être exprimée de manière compacte, y compris les trois racines comme suit :
- .
Si Δ et Δ0 sont nuls, alors l'équation a une racine unique (qui est une racine triple) :
- .
Si Δ = 0 et Δ0 ≠ 0, alors l'équation admet une racine double,
et une racine simple,
- .
Factorisation
Si l'équation cubique ax3 + bx2 + cx + d = 0 a des coefficients entiers et une racine rationnelle, elle peut être trouvée à l'aide du test de racine rationnelle. Ce test peut également être utilisé pour une équation à coefficients rationnels : par multiplication par le plus petit dénominateur commun des coefficients, on obtient une équation à coefficients entiers qui a exactement les mêmes racines.
Trouver une racine permet de trouver les deux autres racines en factorisant puis en résolvant une équation quadratique, ce qui permet d'écrire toutes les racines sans utiliser de racines cubiques : si r est une racine de l'équation cubique, alors nous pouvons mettre en facteur x − r, par exemple en utilisant une division polynomiale, pour obtenir
- .
Par conséquent, si nous connaissons une racine, nous pouvons trouver les deux autres en utilisant la formule quadratique pour trouver les racines de ax2 + (b + ar)x + c + br + ar2, ce qui donne :
pour les deux autres racines.
Cela est particulièrement utile si les coefficients et les trois racines sont réelles, cas où la solution algébrique générale exprime inutilement les racines réelles en termes d'entités complexes[44].
Solution d'Omar Khayyam
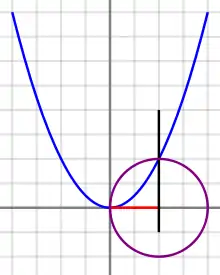
Comme représenté ci-contre, pour résoudre l'équation du troisième degré x3 + m2x = n où n > 0, Omar Khayyam a construit la parabole y = x2/m, le cercle qui de diamètre segment [0, n/m2] sur l'axe des x, et la droite verticale passant par le point au-dessus de l'axe des x où le cercle et la parabole se croisent. La solution est donnée par la longueur du segment de droite horizontal qui joint l'origine à l'intersection de la droite verticale et de l'axe des x.
Une preuve simple et moderne de la méthode est la suivante : en multipliant l'équation par x et en regroupant les termes, nous obtenons
- .
Le membre de gauche est la valeur de y2 sur la parabole. L'équation du cercle étant y2 + x(x − n/m2) = 0, le membre de droite est la valeur de y2 sur le cercle.
Solution par trisection de l'angle
Une équation cubique à coefficients réels peut être résolue géométriquement en utilisant la règle, le compas et la trisection de l'angle, si et seulement si l'équation admet trois solutions réelles[45].
Applications
Les équations cubiques apparaissent dans divers contextes.
L'aire d'un heptagone régulier peut être exprimée en termes des racines d'une équation cubique. En outre, le rapport des rayons des cercles inscrit et circonscrit du triangle heptagonal est l'une des solutions d'une équation cubique.
Étant donné le cosinus (ou toute autre fonction trigonométrique) d'un angle quelconque, le cosinus d'un tiers de cet angle est l'une des racines d'une équation cubique.
Les valeurs propres d'une matrice 3 × 3 sont les racines d'un polynôme cubique, qui est le polynôme caractéristique de la matrice.
En chimie analytique, l'équation de Charlot, qui peut être utilisée pour trouver le pH des solutions tampons, peut être résolue en utilisant une équation cubique.
En génie chimique et thermodynamique, les équations d'état cubiques sont utilisées pour modéliser le comportement des substances de PVT (pression, volume, température).
Les équations cinématiques impliquant l'évolution des taux d'accélération sont cubiques.
Notes et références
- (en) Jens Høyrup, « The Babylonian Cellar Text BM 85200 + VAT 6599 Retranslation and Analysis », dans Amphora: Festschrift for Hans Wussing on the Occasion of his 65th Birthday, Birkhäuser, (ISBN 978-3-0348-8599-7, DOI 10.1007/978-3-0348-8599-7_16), p. 315-358.
- (en) Kangshen Shen, John N. Crossley (en) et Anthony Wah-Cheung Lun, The Nine Chapters on the Mathematical Art : Companion & Commentary, Oxford University Press, (ISBN 978-0-19-853936-0, lire en ligne), p. 177.
- (en) B. L. van der Waerden, Geometry and Algebra of Ancient Civilizations, Springer, (lire en ligne), chap. 4.
- (en) Roger Cooke, The History of Mathematics : A Brief Course, Wiley, , 648 p. (ISBN 978-1-118-46029-0, lire en ligne), p. 63.
- (en) Karen Rea Nemet-Nejat, Daily Life in Ancient Mesopotamia, GPG, , 346 p. (ISBN 978-0-313-29497-6, lire en ligne), p. 306.
- (en) Roger Cooke, Classical Algebra : Its Nature, Origins, and Uses, Wiley, , 224 p. (ISBN 978-0-470-27797-3, lire en ligne), p. 64.
- Selon (en) Lucye Guilbeau, « The history of the solution of the cubic equation », Mathematics News Letter, vol. 5, no 4, , p. 8-12 (DOI 10.2307/3027812, JSTOR 3027812) : « the Egyptians considered the solution impossible, but the Greeks came nearer to a solution ».
- Guilbeau 1930, p. 8-9.
- (en) T. L. Heath, The Works of Archimedes, Cambridge University Press, (lire en ligne).
- (en) Thomas L. Heath, Diophantus of Alexandria : A Study in the History of Greek Algebra, Martino Pub, , 396 p. (ISBN 978-1-57898-754-2, lire en ligne), p. 87-91.
- (en) Yoshio Mikami, The Development of Mathematics in China and Japan, Chelsea Publishing Company, , 2e éd. (1re éd. 1913) (ISBN 978-0-8284-0149-4), chap. 8 (« Wang Hsiao-Tung and Cubic Equations »), p. 53-56.
- (en) « A paper of Omar Khayyam », Scripta Math., vol. 26, , p. 323-337.
- Selon (en) John J. O'Connor et Edmund F. Robertson, « Omar Khayyam », sur MacTutor, université de St Andrews : « This problem in turn led Khayyam to solve the cubic equation x3 + 200x = 20x2 + 2000 and he found a positive root of this cubic by considering the intersection of a rectangular hyperbola and a circle. »
- Selon O'Connor et Robertson, « Omar Khayyam » , op. cit. : « Khayyam himself seems to have been the first to conceive a general theory of cubic equations ».
- Selon Guilbeau 1930, p. 9 : « Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics ».
- (en) Bibhutibhusan Datta (en) et Avadhesh Narayan Singh (de), History of Hindu Mathematics: A Source Book (en), vol. 2 : Algebra, (lire en ligne), « Equation of Higher Degree », p. 76.
- (en) John J. O'Connor et Edmund F. Robertson, « Sharaf al-Din al-Muzaffar al-Tusi », sur MacTutor, université de St Andrews.
- (en) J. L. Berggren, « Innovation and tradition in Sharaf al-Dīn al-Ṭūsī's Muʿādalāt », JAOS, vol. 110, no 2, , p. 304-309 (JSTOR 604533).
- (en) John J. O'Connor et Edmund F. Robertson, « Leonardo Pisano Fibonacci », sur MacTutor, université de St Andrews.
- Tartaglia, Hamon et Degryse 2010, p. 12.
- Serfati 1992, p. 7.
- (en) John J. O'Connor et Edmund F. Robertson, « History of quadratic, cubic and quartic equations », sur MacTutor, université de St Andrews.
- Serfati 1992, p. 8.
- Encyclopaedia Universalis, del Ferro Scipione
- (en) M. Kline, Mathematical Thought from Ancient to Modern Times, New York, Oxford University Press, (lire en ligne), p. 263.
- Nordgaard 1938, p. 331.
- Nordgaard 1938, p. 332.
- Serfati 1992, p. 9.
- Nordgaard 1938, p. 333.
- Serfati 1992, p. 12.
- Serfati 1992, p. 15.
- Serfati 1992, p. 14.
- Denis Daumas, «Dimissis incruciationibus» ou la première apparition d'une racine carrée d'une quantité moindre que zéro, Irem de la Réunion
- Nickalls, R. W. D. (July 2006), "Viète, Descartes and the cubic equation" (PDF), Mathematical Gazette, 90: 203–208
- (la) L. Euler, « De formis radicum aequationum cujusque ordinis conjectatio », dans Comment. Petropol. 1732-1733 (publié en 1738), vi, p. 216-231 (E30), traduction en anglais disponible sur arXiv:0806.1927
- (en) David Eugene Smith, History of mathematics, vol. 2, Dover, 1958 (1re éd. 1925) (ISBN 978-0-48620430-7), p. 464
- Pour plus de détails,
- Cette égalité est mentionnée dans l'introduction de (en) Israel Gelfand, Mikhail Kapranov (de) et Andrei Zelevinsky, Discriminants, Resultants, and Multidimensional Determinants, Springer, coll. « Modern Birkhäuser Classics », (1re éd. 1994) (ISBN 978-0-8176-4770-4, lire en ligne), p. 1 et démontrée par exemple dans la ., liée en bas de cette page.
- Pour une démonstration, voir par exemple la même section « Discriminant d'un polynôme de degré 3 » de la leçon « Équation du troisième degré » sur Wikiversité .
- Amine Marrakchi, « Résolution des équations de degré 3 et 4 », sur Images des mathématiques, .
- Pour voir le chapitre « Résolutions trigonométriques » de la leçon sur Wikiversité, suivre le lien en bas de cette page.
- (en) J. Plante, « Cubic Equations from an Analytic Point of View », Amer. Math. Monthly, vol. 125, no 9, , p. 845-849 (DOI 10.1080/00029890.2018.1507207)
- (en) W. H. Press, S. A. Teukolsky, W. T. Vetterling et B. P. Flannery, Numerical Recipes: The Art of Scientific Computing, Cambridge University Press, , 3e éd., 1235 p. (ISBN 978-0-521-88068-8, lire en ligne), p. 228
- (en) Sara Confalonieri, « The casus irreducibilis in Cardano's Ars Magna and De Regula Aliza », Arch. Hist. Exact Sci., vol. 69, no 3, (DOI 10.1007/s00407-015-0149-9).
- (en) Andrew M. Gleason, « Angle trisection, the heptagon, and the triskaidecagon », Amer. Math. Monthly, vol. 95, no 3, , p. 185-194 (DOI 10.1080/00029890.1988.11971989), Thm. 1.
Voir aussi
Articles connexes
Liens externes
- (en) John J. O'Connor et Edmund F. Robertson, « History of quadratic, cubic and quartic equations », sur MacTutor, université de St Andrews.
- Gérard Villemin, « Équations du troisième degré », sur Nombres - Curiosités, théorie et usages
- (en) « Background of Quadratic Equations », sur mathforcollege.com
Bibliographie
- Michel Serfati, « Le secret et la règle », Séminaire de Philosophie et Mathématiques, no 6, , p. 1-39 (lire en ligne, consulté le )
- Niccolo Tartaglia, Gérard Hamon et Lucette Degryse, Questions et inventions diverses, livre IX : L'invention de la résolution des équations du troisième degré, Paris, Hermann, coll. « Histoire des sciences », , 251 p. (ISBN 978-2-7056-7034-4, présentation en ligne)
- (en) Martin A. Nordgaard, « Sidelights on the Cardan-Tartaglia controversy », National Mathematics Magazine, vol. 12, no 7, , p. 327-346 (lire en ligne)
- (en) William S. Anglin et Joachim Lambek, The Heritage of Thales, Springer, (lire en ligne), « 24 et 25 »
- (en) T. Dence, « Cubics, chaos and Newton's method », The Mathematical Gazette, vol. 78, no 492, , p. 347-348 (DOI 10.2307/3619617)
- (en) R. Dunnett, « Newton-Raphson and the cubic », The Mathematical Gazette, vol. 78, no 483, , p. 347-348 (DOI 10.2307/3620218)
- (en) Douglas W. Mitchell, « Solving cubics by solving triangles », The Mathematical Gazette, vol. 91, no 522, , p. 514-516
- (en) Douglas W. Mitchell, « Powers of φ as roots of cubics », The Mathematical Gazette, vol. 93, no 528, , p. 481-482
















![{\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {{\Delta _{1}}^{2}-4{\Delta _{0}}^{3}}}}{2}}}}](https://img.franco.wiki/i/092df4c334febe4d1f4729d8f428fb8322f28e26.svg)







