Niccolò Fontana Tartaglia
Niccolò Fontana dit Tartaglia (« Le Bègue »), né à Brescia en 1499 et mort à Venise le , est un mathématicien italien.

| Naissance | |
|---|---|
| Décès | |
| Nom de naissance |
Niccolò Fontana |
| Activités | |
| Père |
Micheletto Fontana (d) |

Tartaglia, pas Fontana
Tartaglia ne connaissait pas le nom de famille de son père.
Il mentionne dans son dernier testament (du , il meurt trois jours après) Zuampiero Fontana comme son « frère charnel légitime ». Plusieurs chercheurs en ont conclu — à tort — que Fontana était le vrai nom de famille de Tartaglia, qui a pourtant toujours signé ses lettres et ouvrages par Nicolo Tartalea (jusqu'en 1550), puis Nicolo Tartaglia.
Biographie
Niccolò Fontana est issu d'une famille pauvre. Son père, Micheletto, meurt lorsqu'il a six ans.
Lors du sac de Brescia par les Français en 1512, il se réfugie avec sa mère et sa sœur dans la cathédrale pour échapper aux envahisseurs. Rien n'y fait, les soldats de Louis XII pénètrent dans le lieu sacré, dans lequel se sont réfugiés certains insurgés, dont Niccolò. Il est laissé pour mort, avec une fracture du crâne et un coup de sabre à travers la mâchoire et le palais : bouche tailladée, dents brisées, maxillaires et palais fracturés...
« Le plus dur est que ma mère ne pouvant acheter des onguents comme il se doit (ni appeler un médecin), fut contrainte de me soigner tout le temps de ses propres mains, […] en nettoyant souvent les blessures, prenant exemple des chiens qui, quand ils se retrouvent blessés, se soignent seulement en tenant leur blessure propre avec la langue[1]. »
La blessure au palais lui laisse un défaut d'élocution qui mettra du temps à disparaître, ce qui lui vaut son surnom « Tartaglia » [tar'ta:ʎ:a] par ses camarades, tartagliare signifiant bégayer en italien. C'est Niccolò lui-même qui choisira de faire de ce surnom — d'abord Tartalea jusqu'en 1550, puis Tartaglia — son nom (à l'époque, il était habituel de ne pas avoir de nom de famille[2]) :
« Comme ce surnom m'est resté très longtemps, pour garder le souvenir de mon malheur, j'ai voulu m'appeler Nicolo Tartaglia[3]. »
Lorsqu'il a environ 14 ans, sa mère économise pour permettre à son fils de suivre l'école d'écriture d'un certain maître Francisco, pendant quinze jours.
Devenu adulte, il gagne sa vie en enseignant les mathématiques dans différentes villes d'Italie et en participant à des concours.
En 1535, lors d'une confrontation avec Antonio Maria Del Fiore (it) (un des élèves de Scipione del Ferro), on lui propose trente équations du troisième degré du type x3 + px = q. Les résolutions ne se font, à l'époque, qu'à tâtons. Dans la nuit du 12 au , juste avant la date limite, Tartaglia aurait trouvé la résolution générale de ce type d'équation, et résolu les trente équations en quelques heures. Ce n'est d'ailleurs que pour l'honneur, puisqu'il renonce au prix — trente banquets successifs. Dans l'espoir de gagner d'autres concours, Tartaglia ne dévoile pas sa formule. Cardan, mis au courant de ce succès, fait venir Tartaglia à Milan et le persuade de lui révéler sa méthode, en promettant de ne jamais la dévoiler et a fortiori la publier. Celui-ci cède. Cardan est alors en possession de la solution générale des équations du troisième degré. Apprenant que Scipione del Ferro a donné la solution avant Tartaglia, il se sent délié de sa promesse et publie le résultat dans Ars Magna en 1545.
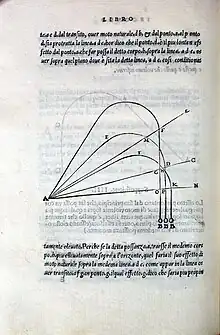
On doit aussi à Tartaglia des résultats en sciences de l'artillerie avec les courbes balistiques mais il s’en tire maladroitement sur le problème de la portée maximale[4]. En la matière, sa pensée est encore largement imprégnée de la théorie de l'impetus avec l'usage de l'équerre, l'angle de 45° et une courbe en trois parties dont une verticale, la pesanteur agissant sur toute la trajectoire[4]. Il rédigea également un traité sur les opérations numériques à l'usage du commerce et, en 1543, des traductions d'Euclide et d'Archimède.
Œuvres

- La Nova Scientia (Venise, 1537)
- L'Euclide Megarese (Venise, 1543)
- Le opera archimedis (1543)
- Quesiti et inventioni diverse (Venise, 1546)
- Le risposte a Ludovico Ferrari (1547-1548)
- La travagliata Inventione (1551)
- Il general trattato di numeri e misure (1556-1560) [lire en ligne] sur le SCD de l'université de Strasbourg
- De insidentibus aquæ et De ponderositate (publication posthume en 1565)
Notes et références
- (it) Nicolo Tartaglia, Quesiti et inventioni diverse (lire en ligne), p.69 (p.144 du fichier pdf)
- (en) « Who Is Tartaglia Really? - Do Not Call Nicolo Tartaglia Fontana! »
- Tartaglia & G. Hamon & L. Degryse, Questions et inventions diverses, livre IX : ou L'invention de la résolution des équations du troisième degré, Paris, Hermann, , 251 p. (ISBN 978-2-7056-7034-4), p. 201
- Bertrand Gille, « Histoire des techniques », dans Annuaire 1976/1977 de l'EPHE, IVe section, sciences historiques et philologiques, (lire en ligne), p. 723-786 (p. 778).
Bibliographie
- Source principale (apparemment) : Bertrand Hauchecorne et Daniel Surratteau, Des mathématiciens de A à Z, Éditions Ellipses, 2008, 4e éd.
- (en) William Dunham, Journey through Genius, John Wiley & Sons, 1990 (ISBN 0-471-50030-5), chap. 6 (« Cardano and the solution of the cubic »)
- Bertrand Gille (dir.), Histoire des techniques, Paris, Gallimard, coll. « La Pléiade », 1978 (ISBN 978-2-07-010881-7)