Conique

On obtient une conique en prenant l'intersection d'un plan avec un cône dont la courbe directrice est un cercle. On peut, dans l'étude, se limiter à l'intersection d'un plan avec un cône de révolution.

Selon les positions relatives du plan de coupe et du cône de révolution, on obtient[1] différents types de coniques :

Exemples de coniques dégénérées.

• Des coniques propres, quand le plan de coupe ne passe pas par le sommet du cône. On distingue trois sortes de coniques propres en fonction de l'angle d'inclinaison du plan de coupe avec l’axe du cône :
  • si cet angle d'inclinaison est inférieur à l'angle d'ouverture (angle formé par l'axe du cône et une génératrice), l'intersection est une hyperbole ;
  • si cet angle d'inclinaison est égal à l'angle d'ouverture du cône, l'intersection est une parabole ;
  • si cet angle d'inclinaison est supérieur à l'angle d'ouverture du cône, l'intersection est une ellipse ;
  • dans le cas maximal où l'angle d'inclinaison du plan de coupe est droit, cette ellipse est même un cercle.
• Des coniques dégénérées (en), quand le plan contient le sommet du cône. Là encore, on distingue trois sortes de coniques dégénérées en fonction de l'angle d’inclinaison du plan de coupe avec l’axe du cône :
  • si cet angle d'inclinaison est inférieur à l'angle d'ouverture du cône, l'intersection est réduite à un couple de droites sécantes (deux génératrices du cône).
  • si cet angle d'inclinaison est égal à l'angle d'ouverture du cône, l'intersection est réduite à une seule droite (une des génératrices du cône là où le plan de coupe et le cône sont tangents) ;
  • si cet angle d'inclinaison est supérieur à l'angle d'ouverture du cône, l'intersection est réduite à un seul point (le sommet du cône).

La définition par foyer et directrice des coniques est encore appelée définition monofocale de ces coniques.

Quatre coniques ayant même foyer et même directrice.

Dans un plan (p), on considère une droite (D) et un point F non situé sur (D). Soit e un réel strictement positif.

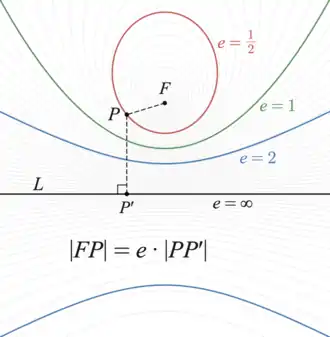
On appelle conique de droite directrice (D), de foyer F et d'excentricité e l'ensemble des points M du plan (p) vérifiant[2] :

${\displaystyle [1]\qquad \mathrm {d} (M,F)=e\mathrm {d} (M,(\mathrm {D} ))}$

où

${\displaystyle \mathrm {d} (M,F)}$ mesure la distance du point M au point F

et

${\displaystyle \mathrm {d} (M,(\mathrm {D} ))}$ mesure la distance du point M à la droite (D)

Le paramètre e définit la forme de la conique, c'est-à-dire que deux coniques ayant même excentricité sont image l'une de l'autre par une similitude.

• Si e < 1, on obtient une courbe fermée et bornée (ellipse).
• Si e = 1, on obtient une courbe ouverte et infinie (parabole).
• Si e > 1 on obtient une courbe possédant deux branches symétriques par rapport au point d'intersection de leurs asymptotes communes (hyperbole).

Toutes ces courbes possèdent comme axe de symétrie la droite passant par F et perpendiculaire à (D) appelé axe principal de la conique.

Coniques

On note K le projeté orthogonal du point F sur la droite (D) et h la distance de K à F (le produit p = eh s'appelle le paramètre de la conique depuis Pierre Hérigone).

Pour tout point O de l'axe principal, on peut construire le repère orthonormal ${\displaystyle (O,{\vec {u}},{\vec {v}})}$ où ${\displaystyle {\vec {u}}={\frac {1}{h}}{\overrightarrow {KF}}}$ dans lequel F a pour abscisse α.

Pour un point M de coordonnées (x , y) on peut exprimer les distances précédentes à l'aide des deux formules suivantes : ${\displaystyle [2]\qquad \mathrm {d} (M,F)={\sqrt {(x-\alpha )^{2}+(y-0)^{2}}}}$ ${\displaystyle [3]\qquad \mathrm {d} (M,(\mathrm {D} ))={\sqrt {(x-\alpha +h)^{2}}}}$ ce qui implique en élevant [1] au carré et en utilisant [2] et [3] : ${\displaystyle [4]\qquad (x-\alpha )^{2}+y^{2}=e^{2}(x-\alpha +h)^{2}}$ soit après réduction : ${\displaystyle [5]\qquad x^{2}(1-e^{2})+y^{2}=2Bx+C}$ où ${\displaystyle B=(1-e^{2})\alpha +ep\quad C=(p-e\alpha )^{2}-\alpha ^{2}}$. Un choix judicieux de O permet de simplifier cette équation.

En prenant ${\displaystyle \alpha ={\frac {p}{1+e}}}$, le coefficient C s'annule et O est un point de la conique appelé sommet. L'équation s'écrit : ${\displaystyle x^{2}(1-e^{2})+y^{2}=2px}$.

En particulier, dans le cas où e = 1, on retrouve l'équation caractéristique de la parabole[3] :

${\displaystyle y^{2}=2px}$.

Dans le cas où e est différent de 1, pour ${\displaystyle \alpha ={\frac {ep}{e^{2}-1}}}$, le coefficient B s'annule et le point O est centre de symétrie de la conique. L'équation s'écrit : ${\displaystyle x^{2}(1-e^{2})+y^{2}={\frac {p^{2}}{1-e^{2}}}}$, dans laquelle on retrouve, en posant ${\displaystyle a^{2}={\frac {p^{2}}{(1-e^{2})^{2}}}\quad b^{2}=\left|{\frac {p^{2}}{1-e^{2}}}\right|}$, les équations caractéristiques suivantes[4] :

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$ pour e < 1 — cas de l'ellipse

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ pour e > 1 — cas de l'hyperbole

Dans les équations précédentes, on trouve l'équation d'un cercle de rayon r dans le cas où e = 0 et p = r. On considère alors le cercle comme un cas particulier d'ellipse d'excentricité nulle, dont le foyer est situé au centre du cercle et dont la directrice est envoyée à l'infini[4].

Dans le repère d'origine F et de direction ${\displaystyle {\vec {w}}={\frac {1}{h}}{\overrightarrow {FK}}}$, une telle conique a pour équation polaire[5] : ${\displaystyle \rho ={\frac {p}{1+e\cos(\theta )}}}$

Réciproquement, toute courbe dont l'équation polaire dans un repère ${\displaystyle (O,{\vec {u}},{\vec {v}})}$ est : ${\displaystyle \rho ={\frac {p}{A\cos(\theta )+B\sin(\theta )+1}}}$, où p est un réel non nul, et (A, B) un couple de réels différent de (0, 0), est une conique de foyer O, d'excentricité ${\displaystyle {\sqrt {A^{2}+B^{2}}}}$ et d'axe la droite d'équation Ay = Bx[3].

Cette forme d'équation polaire est utile dans l'étude de la trajectoire des planètes[3].

Ellipse : MF + MF' = constante

Hyperbole : abs(MF - MF') = constante

L'ellipse peut être définie comme le lieu des points M dont la somme des distances MF et MF' à deux points fixes F et F', appelés foyers de l'ellipse, est constante et égale à une valeur fixée. Cette définition reste valable dans le cas du cercle, pour lequel les foyers sont confondus.

L'hyperbole peut être définie comme le lieu des points M dont la valeur absolue de la différence des distances MF et MF' à deux points fixes F et F', appelés foyers de l'hyperbole, est constante et égale à une valeur fixée.

La parabole n'a pas de définition bifocale.

Cette propriété bifocale correspond à une autre définition d'une conique par un point et une courbe directrice[6] - [7] : l’ensemble des centres des cercles passant par un point fixe F et tangent à, soit un cercle fixe (C) ne passant pas par F, soit une droite fixe (D) ne contenant pas F, est une conique de foyer F et de courbe directrice (C) ou (D).

Si F est intérieur à (C), la courbe est une ellipse ; si F est extérieur à (C) la courbe est une hyperbole ; si la directrice est une droite, la courbe est une parabole.

En notant F' le centre du cercle (C) et 2a son rayon (a > 0), on obtient en effet :

• dans le cas de l'ellipse, le cercle centré en M est tangent intérieurement à (C), et le point M vérifie MF + MF' = 2a ;
• dans le cas de l'hyperbole, le cercle (C) est tangent au cercle centré en M, soit intérieurement, et le point M vérifie MF – MF' = 2a, soit extérieurement, et le point M vérifie MF' – MF = 2a. On regroupe les deux cas par la condition |MF – MF'| = 2a.

Les points F et F' sont les foyers de la conique.

Quant à la parabole, on retrouve, pour le cercle centré en M passant par F et tangent à (D), l'égalité MF = d(M,(D)).

Les paraboles admettent un et un seul couple foyer/directrice au sens de la définition monofocale, et l'excentricité correspondante vaut 1.

Ellipses et hyperboles admettent exactement deux couples foyer/directrice au sens de la définition monofocale, et ceux-ci correspondent à une même valeur de l'excentricité. Ils sont symétriques par rapport au centre de l'ellipse ou au point d'intersection des asymptotes de l'hyperbole. Ces foyers sont les points intervenant dans la définition bifocale.

Les foyers et les directrices des coniques peuvent être déterminés géométriquement dans le cadre de la définition des coniques comme intersection d'un cône et d'un plan ne passant pas par le centre de celui-ci.

Il existe, selon l'orientation du plan par rapport à l'axe du cône, une (cas des paraboles) ou deux (cas des ellipses et des hyperboles) sphères tangentes à la fois au plan et au cône ; ce sont des sphères centrées sur l'axe, situées dans un même demi-cône (cas des ellipses) ou dans des demi-cônes opposés (cas des hyperboles).

Chacune de ces sphères définit l'un des foyers de la conique (c'est le point de tangence de la sphère et du plan) ainsi que la droite directrice associée (c'est l'intersection du plan de la conique et du plan contenant le cercle de tangence de la sphère et du cône) ; c'est le théorème de Dandelin.

Une conique étant donnée, avec son équation dans un repère quelconque, on cherche à déterminer un repère orthonormal dans lequel l'équation de la conique serait aussi simple que possible. On se place d'emblée dans le cas où l'équation est donnée dans un repère orthonormal, si ce n'est pas le cas, on peut s'y ramener par changement de base. On peut également éliminer le terme en xy en changeant de base par rotation[9].

En effet, les équations de changement de base, pour une rotation d'angle θ, sont : ${\displaystyle {\begin{cases}x=\cos(\theta )X-\sin(\theta )Y\\y=\sin(\theta )X+\cos(\theta )Y.\end{cases}}}$

Le coefficient devant XY s'écrit alors : ${\displaystyle (C-A)\sin(2\theta )+2B\cos(2\theta )}$ et si B est non nul, ce coefficient s'annule lorsque 2θ est un argument de C – A – 2Bi

On suppose désormais que la conique a pour équation :

${\displaystyle A_{1}x^{2}+C_{1}y^{2}+2D_{1}x+2E_{1}y+F=0}$

et l'on distingue trois éventualités[9].

Un changement d'origine en prenant O₁(− D₁/A₁,− E₁/C₁) permet d'éliminer les termes en x et y. La conique a pour équation dans ce nouveau repère : ${\displaystyle A_{1}x^{2}+C_{1}y^{2}+F_{1}=0}$ Trois cas se présentent alors :

• si F₁ est de signe opposé à A₁ et C₁, en posant a² = − F₁/A₁ et b² = − F₁/C₁, on obtient l'équation réduite d'une ellipse ;

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

• si F₁ est nul, la conique est réduite à un point : O₁ ;
• si F₁ est de même signe que A₁ et C₁, la conique est vide.

Le même changement de repère conduit à l'équation : ${\displaystyle A_{1}x^{2}+C_{1}y^{2}+F_{1}=0}$ et l'on peut même, en permutant éventuellement les vecteurs de la base, supposer que C₁F₁ ≥ 0. Deux cas se présentent alors :

• si F₁ est non nul, en posant a² = − F₁/A₁ et b² = F₁/C₁, on obtient l'équation réduite d'une hyperbole ;

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ ;

• si F₁ est nul, en posant a² = |1/A₁| et b² = | 1/C₁|, la conique est la réunion de deux droites sécantes d'équations : bx ± ay = 0.

On peut, en permutant éventuellement les vecteurs de la base, supposer que A₁ est nul et C₁ non nul. Un changement d'origine en prenant O₁(0, −E₁/C₁) conduit à l'équation ${\displaystyle C_{1}y^{2}+2D_{1}x+F_{1}=0,}$ et deux cas se présentent :

• si D₁ est non nul, le changement d'origine en prenant O₂(−F₁/(2D₁), 0) permet d'éliminer le terme constant. Ensuite, en posant p = − D₁/C₁, on obtient l'équation réduite d'une parabole

${\displaystyle y^{2}=2px}$ ;

• si D₁ est nul, l'équation se réduit à${\displaystyle C_{1}y^{2}+F_{1}=0}$et l'on distingue trois sous-cas :
  • si F₁ est de signe opposé à C₁, en posant p² = − F₁/C₁ la conique est la réunion de deux droites parallèles d'équations y = ± p,
  • si F₁ est nul, la conique se réduit à une droite d'équation y = 0,
  • si F₁ est de même signe que C₁, la conique est vide.

Ces équations réduites permettent de mettre en évidence les orbites des coniques pour les isométries : toutes les coniques d'une même classe avec les mêmes paramètres sont isométriques.

On se place dans le cadre d'un plan affine réel muni d'un repère et on considère l'ensemble des fonctions f définies pour tout point M(x, y) par ${\displaystyle f(M)=Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F}$ où A, B, C, D, E, F sont des constantes réelles telles que (A,B,C) ≠ (0,0,0).

On note C_f la conique d'équation f(M) = 0. La question qui se pose est de savoir quel est l'effet des transformations affines sur la conique C_f, plus exactement de déterminer son orbite pour les transformations affines. Pour deux coniques C_f1 et C_f2, on observe que s'il existe une transformation affine et un réel λ non nul tels que f₁ ∘ φ = λf₂, alors φ(C_f2) = C_f1. On dit alors que f₁ et f₂ sont affinement équivalentes. Le but de la classification affine est de ranger les fonctions f en classe d'équivalence[10].

On définit pour cela

• ${\displaystyle Q_{f}={\begin{pmatrix}A&B\\B&C\end{pmatrix}}}$
• ${\displaystyle L_{f}={\begin{pmatrix}2D&2E\end{pmatrix}}}$
• ${\displaystyle M_{f}={\begin{pmatrix}A&B&D\\B&C&E\\D&E&F\end{pmatrix}}}$
• ${\displaystyle X={\begin{pmatrix}x\\y\end{pmatrix}}}$
• ${\displaystyle {\tilde {X}}={\begin{pmatrix}x\\y\\1\end{pmatrix}}}$

On obtient les écritures matricielles de f suivantes ${\displaystyle f(M)=^{\operatorname {t} }XQ_{f}X+L_{f}X+F=^{\operatorname {t} }{\tilde {X}}M_{f}{\tilde {X}}}$

On démontre ensuite que f₁ et f₂ sont affinement équivalentes si et seulement si Q_f1 et Q_f2 ont même signature (à l'ordre près) ainsi que M_f1 et M_f2. De plus la signature de Q_f (à l'ordre près) caractérise le signe de son déterminant AC -B². On obtient alors une classification des coniques en fonction des signatures de ces deux matrices :

Quand le déterminant de M_f est nul, on dit que la conique est dégénérée[11].

En géométrie projective, les coniques sont encore les courbes planes algébriques du second degré, c'est-à-dire les courbes planes caractérisées dans un certain repère projectif par une équation polynomiale homogène de degré 2. Une telle équation a pour forme (voir coordonnées homogènes)

${\displaystyle AX^{2}+2BXY+CY^{2}+2DXZ+2EYZ+FZ^{2}=0}$

avec A, B et C non tous nuls[12].

Les coordonnées (X, Y,Z) d'un point dans un repère de l'espace projectif ne sont pas toutes nulles, et deux triplets de coordonnées proportionnelles définissent le même point. On travaille plus précisément dans le plan projectif réel P(E), où E est l'espace vectoriel réel de dimension 3. Une conique projective réelle est une courbe qui possède une équation polynomiale homogène du second degré dans un repère projectif de P(E).

Même pour les coniques réelles (les coefficients A, B, C, D, E, F ci-dessus sont réels), il peut être utile de considérer le complexifié P(E_C) de P(E), qui est le plan projectif complexe. Un repère de P(E) est aussi un repère de P(E_C), les coordonnées étant complexes. Les points réels sont ceux de P(E), les points imaginaires ceux de P(E_C) qui ne sont pas dans P(E). Les points imaginaires sont ceux qui ont au moins une coordonnée non réelle dans un repère de P(E) (ceci ne dépend pas du repère). Sauf précision, les points de la conique sont les points réels qui satisfont l'équation, mais on peut parler des points imaginaires d'une conique réelle[12].

Les coordonnées homogènes sont les coordonnées dans la base de E déterminée par le repère projectif choisi. On voit alors qu'une conique de P(E) est définie par une forme quadratique sur E. Plus précisément la conique (C_q) de P(E) associée à une forme quadratique q de E est l'ensemble des points de P(E) déterminés par des vecteurs non nuls u de E tels que q(u) = 0. Deux formes quadratiques proportionnelles définissent la même conique[12].

Une conique est dite propre si elle est associée à une forme quadratique non dégénérée, dégénérée sinon. Une forme quadratique dégénérée est soit le carré d'une forme linéaire, soit la somme ou la différence de carrés de formes linéaires. Elle se factorise donc toujours comme produit de deux formes linéaires (éventuellement complexes). Les noyaux de ses formes linéaires sont des plans qui définissent des droites projectives (éventuellement complexes). Une conique dégénérée réelle non vide (sur l'espace réel) est donc soit une droite, soit la réunion de deux droites (éventuellement complexes)[13].

L'image d'une conique par une homographie est encore une conique, puisque celle-ci correspond à une transformation linéaire f sur E, si la conique est associée à la forme quadratique q, l'image de celle-ci est associée à la forme quadratique q ∘ f⁻¹[13].

La classification projective des coniques est la classification à homographie près : deux coniques sont dans la même classe si l'une est image de l'autre par une homographie. Elle se déduit donc de la classification des formes quadratiques, sachant que deux coniques proportionnelles (opposées en particulier) définissent la même conique. La classification projective des coniques réelles s'obtient alors directement à partir de celle des formes quadratiques réelles donnée par la loi d'inertie de Sylvester. Autrement dit, l'orbite d'une conique réelle sous l'action du groupe projectif linéaire PGL(3,R) est caractérisée par la signature de la forme quadratique.

Comme deux formes quadratiques opposées sont associées à la même conique, on peut toujours supposer que le premier terme de la signature est supérieur ou égal au second.

Par diagonalisation des formes quadratiques, par exemple par réduction de Gauss, on obtient une écriture de celle-ci comme somme et/ou différence de carrés qui est déterminée par la signature. La conique est alors l'image par transformation projective d'une conique de l'équation réduite indiquée dans le même repère, ou, de façon équivalente, il existe un repère dans lequel l'équation de la conique est l'équation indiquée.

En particulier, il n'y a à homographie près qu'une seule conique projective réelle non dégénérée non vide, celle qui a pour équation dans un certain repère projectif X²+Y²-Z²=0 (signature (2,1) ou (1,2)). Cette équation est celle d'un cône à base elliptique de sommet l'origine dans l'espace vectoriel E[14].

Un plan affine peut toujours être plongé dans un espace vectoriel E de dimension 3, comme plan affine ne passant pas par l'origine. Un repère de E peut être choisi de façon que le plan affine soit identifié au plan affine d'équation Z = 1 dans ce repère. Ce plan affine apparait alors également comme la partie du plan projectif P(E) formée des points de coordonnées homogènes (X:Y:1), donc par homogénéité ceux de coordonnées (X : Y : Z) avec Z ≠ 0. Les points de coordonnées (X;Y:0) forment alors une droite projective, qui est la droite à l'infini associée au plan affine.

La restriction de la conique projective d'équation

${\displaystyle AX^{2}+2BXY+CY^{2}+2DXZ+2EYZ+FZ^{2}=0}$

au plan affine Z = 1, a pour équation, en choisissant le repère affine déduit du repère projectif

${\displaystyle AX^{2}+2BXY+CY^{2}+2DX+2EY+F=0}$

et l'on a bien l'équation d'une conique affine, et par l'opération inverse, en homogénéisant l'équation de la conique affine, celle-ci apparaît comme la restriction au plan affine d'une conique projective.

L'intersection de la conique projective avec la droite à l'infini associée au plan affine a pour équation

${\displaystyle AX^{2}+2BXY+CY^{2}=0}$.

Le trinôme AX² + 2BXY + CY² est la forme quadratique à l'infini de la conique affine. Le nombre de solutions de l'équation à homogénéïté près est le nombre de point à l'infini de la conique. Celui-ci est 0, 1, ou 2, suivant le signe de B² -AC, discriminant (réduit) de l'équation (en Y/X ou X/Y suivant que l'on cherche des solutions telles que X est non nul ou Y est non nul).

On retrouve alors la classification affine à partir de la classification projective et du nombre de points à l'infini : les critères sont les mêmes, signature de la forme quadratique donnée par l'équation homogénéisée, le discriminant est l'opposé du déterminant de la forme quadratique à l'infini. En particulier une ellipse (B² -AC < 0) n'a pas de point à l'infini, une parabole (B² -AC = 0) a un seul point double à l'infini, c'est-à-dire qu'elle est tangente à la droite à l'infini, une hyperbole (B² -AC > 0) a deux points à l'infini.

En géométrie analytique barycentrique, les coniques sont toujours les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les points ont des coordonnées barycentriques λ, μ et ν qui vérifient une équation polynomiale homogène du second degré de la forme :

${\displaystyle \mathrm {A} _{11}\lambda ^{2}+\mathrm {A} _{22}\mu ^{2}+\mathrm {A} _{33}\nu ^{2}+2\mathrm {A} _{12}\lambda \mu +2\mathrm {A} _{23}\mu \nu +2\mathrm {A} _{31}\nu \lambda =0}$.

On peut identifier cette équation à la précédente, en posant :

${\displaystyle \lambda =\mathrm {X} ,\ \mu =\mathrm {Y} ,\ \nu =\mathrm {Z} }$.

On obtient alors, à un coefficient multiplicatif près :

${\displaystyle \mathrm {A} _{11}=\mathrm {A} ,\mathrm {A} _{22}=\mathrm {C} ,\mathrm {A} _{33}=\mathrm {F} ,\mathrm {A} _{12}=\mathrm {B} ,\mathrm {A} _{23}=\mathrm {E} ,\mathrm {A} _{31}=\mathrm {D} }$.

Le théorème des cinq points, cas particulier du paradoxe de Cramer, permet de montrer qu'il suffit de connaitre cinq points distincts, non alignés trois par trois, pour déterminer de façon unique une conique. Plus précisément, elle sera déterminée de façon unique si aucun sous-ensemble de quatre points n'est aligné, et non dégénérée si et seulement si les cinq points sont non alignés trois par trois.