Pôle et polaire

En géométrie euclidienne, la polaire d'un point par rapport à deux droites sécantes du plan est une droite définie par conjugaison harmonique : les deux droites données, la droite joignant le point à leur intersection, et la polaire forment un faisceau harmonique ; le point est appelé pôle (de cette droite). Cette notion se généralise à celle de polaire par rapport à un cercle, puis par rapport à une conique. La relation entre pôle et polaire est en fait projective : elle est conservée par homographie.

Fig. 1. La polaire du point P par rapport au cercle (C) passe par les points de tangence des droites tangentes à (C) menées par P.

Fig. 2. La polaire du point P est la droite (d). On note qu'elle est perpendiculaire à la droite PO (O centre du cercle (C).

Fig. 3. Pôle P de la droite (d) par rapport à la conique (C). La construction, qui résulte également des propriétés du quadrilatère complet, est calquée sur la précédente.

Définition harmonique

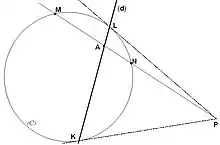
Soient (C) une conique (même dégénérée), et P un point du plan. Considérons un point M mobile sur (C). Soit N le deuxième point d'intersection de (MP) et (C).

Soit enfin A le point tel que P,A,M,N forment une division harmonique, c'est-à-dire tel que le birapport (PA,MN) vaut -1. On montre que, lorsque M varie, le lieu de A est une droite ou un segment de droite.

On appelle polaire de P par rapport à (C) la droite (d) qui porte ce segment. Réciproquement, on dit que P est le pôle de (d) par rapport à (C).

Si la conique est formée de deux droites concourantes en O, OP, (d) et les deux droites forment un faisceau harmonique ; si les deux droites sont parallèles, le faisceau formé par la parallèle passant par P et les trois autres droites est harmonique.

Si la conique est non dégénérée, toute droite admet un pôle.

Dans le cas où (C) est non dégénérée, et si P est extérieur à (C), on peut mener par ce point deux tangentes à la conique. Appelons K et L les points de contact de ces tangentes. Alors, la polaire (d) du point P est la droite (KL) (voir Figure 1 dans le cas d'un cercle). Réciproquement, si une droite coupe la conique, son pôle est l'intersection des deux tangentes aux deux points d'intersection.

Ces définitions montrent que ces notions sont invariantes par homographie, c'est-à-dire que si p est une application projective envoyant la conique (C) sur (C'), et (d) la polaire de P par rapport à (C), la polaire de p(P) par rapport à (C') est p((d)).

Propriétés géométriques dans le cas du cercle

La polaire d'un point P par rapport à un cercle de centre O et de rayon R est une droite perpendiculaire à OP, passant par H situé sur la demi-droite OP tel que OP.OH = R².
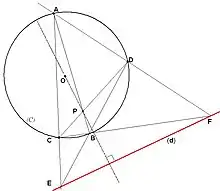
Soient A, B, C, D quatre points d'un cercle (C). On note les points d'intersection
- $P=(AC)\cap (BD)$ ,
- $E=(AB)\cap (DC)$ ,
- $F=(AD)\cap (CB)$ .

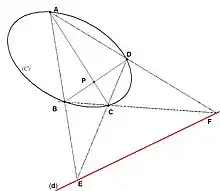
Alors, d'après les propriétés du quadrilatère complet, la polaire de P par rapport à (C) est la droite (FE) (voir Figure 2).

Cette propriété permet de construire la polaire d'un point à la règle uniquement, et aussi de la tracer pour un point intérieur au cercle.

On peut également, en s'aidant de cette propriété, construire à la règle seulement les tangentes à un cercle passant par un point extérieur au cercle.

Généralisation aux coniques projectives

Du fait que les transformations homographiques du plan (c'est-à-dire les perspectives coniques) conservent le birapport, on peut généraliser les propriétés précédentes.

La transformée d'un point par homographie est un point. Celle d'une droite est une droite. Celle d'un cercle est une conique dont la nature dépend de l'homographie. Les homographies conservent les alignements de points et les intersections.

Les propriétés démontrées précédemment par des calculs ou des raisonnements métriques dans le cas du cercle se généralisent donc au cas d'une conique quelconque (et on peut même utiliser un passage à la limite pour traiter le cas d'un couple de droites comme conique dégénérée).

La notion d’extérieur/intérieur, évidente pour l'ellipse, se généralise aux autres coniques (parabole, hyperbole) en définissant l'intérieur par la zone convexe et l’extérieur par son complémentaire.

Si le pôle est à l’extérieur alors sa polaire coupe la conique en 2 points.
Si le pôle est à l’intérieur alors sa polaire est à l’extérieur (et ne coupe pas la conique).
Si le pôle est sur la conique alors sa polaire est la tangente à la conique en ce point.

Utilisation des coordonnées projectives

Soit $C$ la matrice 3×3 associée à la forme bilinéaire symétrique de la conique, d'équation affine $ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0$ ; la forme quadratique correspondante est donc $(X,Y,Z)\mapsto aX^{2}+2bXY+cY^{2}+2dXZ+2eYZ+fZ^{2}$ , et $C={\begin{pmatrix}a&b&d\\b&c&e\\d&e&f\end{pmatrix}}$ . Notant $M$ un point du plan de coordonnées projectives $(X, Y, 1)$ , $M$ appartient à la conique si et seulement si $M T CM = 0$ [1]. Pour tout point $M$ du plan, $CM$ est un vecteur à 3 dimensions ${\begin{pmatrix}p\\q\\r\end{pmatrix}}$ , qui grâce à la dualité projective peut être interprété comme une droite d’équation $pX+qY+r=0$ . Cette droite est la polaire de $M$ (vu ici comme un pôle). Réciproquement si $C$ est inversible (conique non dégénérée), à toute droite (polaire) du plan représentée par un vecteur $D=(a,b,c)^{t}$ , on associe le pôle $M=C^{-1}D$ [2].

Points conjugués

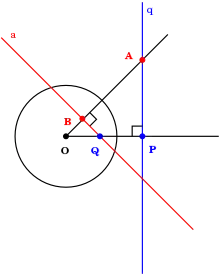
Si un point A appartient à la polaire q du point Q, alors Q appartient à la polaire a de A. Plus généralement, les polaires de tous les points de la droite q passent par son pôle Q.

Soit $x$ et $y$ deux points du plan. Si $y T Cx = 0$ , on dit que les points sont conjugués par rapport à $C$ . On déduit des formules précédentes que $y$ appartient à la polaire de $x$ , et $x$ appartient à la polaire de $y$ . De même (figure ci-contre), les polaires de tous les points d'une droite passent par le pôle de cette droite. C'est cette propriété qui montre que la transformation par polaires réciproques est une involution[2].

Plan projectif complexe

Le cadre le plus naturel pour unifier les résultats précédents est en fait de se placer dans le plan projectif complexe (en) ; il n'apparait alors plus aucune exception pour les coniques non dégénérées (et toutes celles-ci sont isomorphes entre elles). Ainsi, par exemple, la polaire joint toujours les deux points de contact des tangentes, le centre d'un cercle (ou plus généralement d'une conique à centre) a pour polaire la droite de l'infini, etc.[2]

Notes et références

Les points de coordonnées $(X, Y, 0)$ sont les points à l'infini, appartenant à la conique si $aX^{2}+bXY+cY^{2}=0$ .
Jean-Claude Sidler, Géométrie projective, Dunod, 2000 : les définitions sont données page 198.

Bibliographie

Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
Jean Fresnel, Méthodes modernes en géométrie
Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)

Liens externes

Animation interactive à Cut the Knot

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.