Transformation par polaires réciproques

En mathématiques, et plus précisément en géométrie, la transformation par polaires réciproques est une transformation associant à une courbe une autre courbe construite à l'aide des droites tangentes à la première. La courbe image s'appelle la courbe duale de la courbe de départ.

Définition

On considère une courbe plane $Γ 0$ . La courbe polaire au point $M 0 (x 0 (t), y 0 (t))$ de $Γ 0$ par rapport à un cercle (C) (ou de cercle directeur (C)) est l'enveloppe des polaires des points de $Γ 0$ par rapport à (C) ; c'est donc l'ensemble des pôles des tangentes à $Γ 0$ par rapport à (C).

Equations

La polaire par rapport au cercle de centre O et de rayon $r$ et un point $M 0 (x 0, y 0)$ est la droite des points $M (x, y)$ tels que $x 0 x + y 0 y = r 2$ .

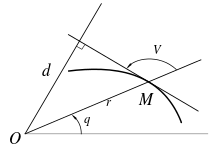
Si $M 0 (x 0 (t), y 0 (t))$ est le point courant d'une courbe $Γ 0$ , le point courant $M (x (t), y (t))$ de la polaire de $Γ 0$ est défini, en coordonnées cartésiennes, par

{\begin{cases}x(t)={\dfrac {r^{2}}{x_{0}(t)y_{0}'(t)-y_{0}(t)x_{0}'(t)}}y_{0}'(t)\\y(t)=-{\dfrac {r^{2}}{x_{0}(t)y_{0}'(t)-y_{0}(t)x_{0}'(t)}}x_{0}'(t)\end{cases}}

soit, en coordonnées complexes :

z(t)=2r^{2}{\frac {z_{0}'(t)}{z_{0}'(t){\overline {z_{0}(t)}}-z_{0}(t){\overline {z_{0}'(t)}}}}.

La « polarisation » échange donc les notions de point d'une courbe et de tangente à la courbe.

Polaire d'une conique

La polaire d'une conique par rapport à un cercle centré en un foyer de la conique est un cercle centré au pôle de la directrice.

Démonstration

L'origine étant prise au foyer, on définit la conique par son équation polaire $\rho ={\frac {p}{1-e\cos \theta }}$ . Le pôle d'une tangente est situé sur la perpendiculaire à celle-ci passant par le foyer (l'origine). Il a donc pour angle polaire $\theta +V+{\frac {\pi }{2}}$ où $V$ désigne l'angle entre $(OM)$ et la tangente.

On sait maintenant que le pôle est en division harmonique avec le projeté du foyer sur la tangente et l'intersection avec le cercle.

La distance du foyer à la tangente vaut $d=\rho \cos(V+{\frac {\pi }{2}})=-\rho \sin V$ le pôle cherché est donc à la distance ${\frac {R^{2}}{d}}$

Les coordonnées du pôle sont donc $x={\frac {R^{2}}{d}}\cos(\theta +V+{\frac {\pi }{2}})={\frac {R^{2}}{\rho }}\left[{\frac {\sin \theta }{\tan V}}+\cos \theta \right]$

et $y={\frac {R^{2}}{d}}\sin(\theta +V+{\frac {\pi }{2}})={\frac {R^{2}}{\rho }}\left[{\frac {\sin \theta }{\tan V}}+\cos \theta \right]$

Mais $\ \tan V={\frac {\rho }{\rho '}}=-{\frac {1-e\cos \theta }{e\sin \theta }}$

d'où $x={\frac {R^{2}}{p}}(1-e\cos \theta )\left[{\frac {e\sin ^{2}\theta }{1-e\cos \theta }}+\cos \theta \right]={\frac {R^{2}}{p}}(\cos \theta -e)$

et $y=-{\frac {R^{2}}{p}}(1-e\cos \theta )\left[-{\frac {e\sin \theta \cos \theta }{1-e\cos \theta }}-\sin \theta \right]=-{\frac {R^{2}}{p}}\sin \theta$

d'où il résulte sans peine : $\left(x+{\frac {eR^{2}}{p}}\right)^{2}+y^{2}={\frac {R^{4}}{p^{2}}}.$

On obtient donc bien un cercle de centre $\left({\frac {eR^{2}}{p}},O\right)$ qui est le pôle de la droite d'équation $X=-{\frac {p}{e}}$ c'est-à-dire la directrice.

Propriétés

La transformation par polaires réciproques est une involution : la polaire d'une polaire par rapport au même cercle est égale à la courbe de départ.
La polaire n'est pas à confondre avec la courbe inverse. D'ailleurs, l'inverse de la polaire par rapport au même cercle est la courbe podaire.
La polaire d'une courbe algébrique est une courbe algébrique dont le degré est égal à la classe de la courbe de départ (c'est-à-dire le degré de l'équation tangentielle).

Exemples

Courbe de départ	Position du centre du cercle directeur par rapport à la courbe de départ	Position du centre du cercle directeur par rapport à la polaire	Polaire
Droite (polaire du point)	Hors de la droite	Différent du point	Point (pôle de la droite)
Conique[1]			Conique
	Foyer de la conique		Cercle
	À l'intérieur de la conique (i.e. dans une région contenant un foyer)		Ellipse
	À l'extérieur de la conique		Hyperbole
	Sur la conique		Parabole
Cardioïde	Point de rebroussement	Foyer au 8/9^e du segment joignant le point double au sommet	Cubique de Tschirnhausen
Cardioïde	Centre du cercle conchoïdal	Foyer	Trisectrice de Maclaurin
Deltoïde	Centre	Sommet	Cubique duplicatrice
Astroïde	Centre	Centre	Cruciforme
Cycloïde à centre	Centre	Centre	Épi
Spirale sinusoïdale de paramètre $α$	Centre	Centre	Spirale sinusoïdale de paramètre $- α / α +1$

Extensions aux surfaces tridimensionnelles

Le concept de polaire réciproque peut être étendu aux surfaces dans l'espace ; la surface transformée devient alors une autre surface[2] - [3].

Voir aussi

Références

Jacques Lenthéric, « Théorie générale des polaires réciproques planes », Nouvelles annales de mathématiques, 1^re série, vol. 8,‎ 1849, p. 252-266
L. Quantin de la Roëre, « Développables formées avec les normales d'une quadrique », Nouvelles annales de mathématiques, 5^e série, vol. 1,‎ 1922, p. 153-159 (lire en ligne)
Pierre Papillon, « Sur les surfaces polaires réciproques des conoïdes », Annales de la faculté des sciences de Toulouse, 3^e série, vol. 25,‎ 1933, p. 239-256 (lire en ligne)

Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4) ;
Bruno Ingrao, Coniques projectives, affines et métriques, Calvage & Mounet, 2011 (ISBN 978-2916352121).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.