Spirale sinusoïdale
En géométrie, les spirales sinusoïdales sont une famille de courbes planes, regroupant de multiples courbes usuelles.
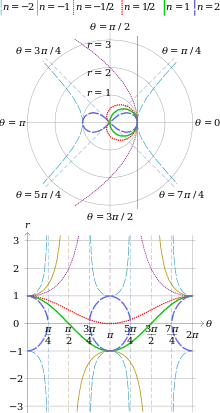
Définitions
Une spirale sinusoïdale peut se définir par son équation polaire :
où a est un réel positif et n un réel.
Propriétés
La courbe est bornée et formée d'un motif de base symétrique défini entièrement pour , fermé si n est positif, à asymptotes si n est négatif. On reconstruit la spirale entière par rotations successives du motif pour les angles , avec k entier.
La spirale sinusoïdale est une courbe algébrique si et seulement si n est un nombre rationnel.
Si n est un entier positif, la spirale sinusoïdale correspondante représente les points dont la moyenne géométrique des distances aux sommets d'un polygone régulier est égale au rayon de ce polygone.
Si n est un entier négatif, la spirale sinusoïdale correspondante représente les points M tels que la moyenne des angles des droites joignant les sommets d'un polygone régulier à M avec une direction fixe est constante.
La longueur de la courbe vaut :
où B désigne la fonction bêta. L'aire contenue par la courbe vaut :
La podaire de la spirale sinusoïdale de paramètre n par rapport à son centre est la spirale sinusoïdale de paramètre n⁄n+1.
Cas particuliers
Pour certaines valeurs bien choisies de n, on reconnait des courbes planes usuelles :
- n=1⁄3 : sextique de Cayley
- n=1⁄2 : cardioïde
- n=1 : cercle
- n=2 : lemniscate de Bernoulli
- n=3 : courbe de Kiepert
- n=-1⁄3 : cubique de Tschirnhausen
- n=-1⁄2 : parabole
- n=-1 : droite
- n=-2 : hyperbole équilatère
- n=-3 : cubique de Kiepert
Liens externes
- Spirale sinusoïdale sur Mathcurve
- (en) Eric W. Weisstein, « Sinusoidal Spiral », sur MathWorld



![{\displaystyle 2a{\sqrt[{n}]{2}}\int _{0}^{\frac {\pi }{2}}\cos ^{{\frac {1}{n}}-1}\theta \,\mathrm {d} \theta =a{\sqrt[{n}]{2}}\,\mathrm {B} \left({\frac {1}{2}},{\frac {1}{2n}}\right)=a{\sqrt[{n}]{2}}{\sqrt {\pi }}{\frac {\Gamma \left({\frac {1}{2n}}\right)}{\Gamma \left({\frac {n+1}{2n}}\right)}},}](https://img.franco.wiki/i/e8f92b0fa0875d51b34af1cf58b2ce3f8342c376.svg)
