Podaire
La podaire d'une courbe C par rapport à un point P est le lieu géométrique des projetés orthogonaux de P sur les tangentes à la courbe C.
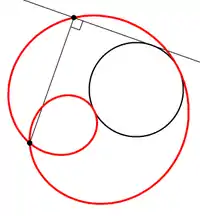
Inversement, la courbe C dont une courbe est la podaire s'appelle l'antipodaire (ou podaire inverse).
L'orthotomique d'une courbe C par rapport à un point P est le lieu géométrique des symétriques de P par rapport aux tangentes à la courbe C. L'orthotomique est donc l'image de la podaire par une homothétie de centre P et de rapport 2.
Étymologie et histoire
La podaire fut étudiée par Colin Maclaurin en 1718 puis par Olry Terquem. Étymologiquement, le terme podaire provient du mot grec podos pied (pied de la perpendiculaire).
Définition mathématique
L'équation paramétrique de la podaire d'une courbe paramétrée c(t) par rapport à un point P est donnée par :
En partant de l'équation cartésienne de la courbe sous la forme F(x, y)=0, en fixant l'origine du repère au point P, si l'équation de la tangente en R=(x0, y0) s'écrit
alors le vecteur (cos α, sin α) est parallèle au segment PX, et la longueur de PX, soit la distance entre la tangente et l'origine, vaut p. Donc X a pour coordonnées polaires (p, α), ce qui permet d'écrire une équation polaire de la podaire.
Exemples
| courbe donnée C |
point de référence P |
courbe podaire |
|---|---|---|
| droite | quelconque | point |
| cercle | sur le cercle | cardioïde |
| cercle | quelconque | limaçon de Pascal |
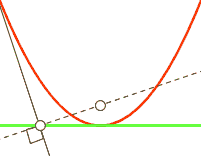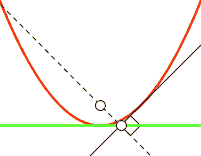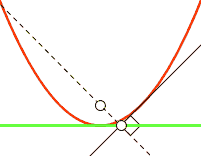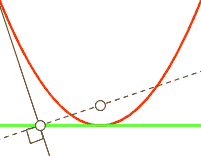
| parabole | foyer | droite |
| parabole | sommet | cissoïde de Dioclès |
| ellipse | foyer | cercle |
| hyperbole équilatère | centre | lemniscate de Bernoulli |
| hyperbole | foyer | cercle |
| spirale logarithmique | pôle | spirale logarithmique |
Applications
La notion de podaire peut être utilisée en mécanique du point pour l'étude des mouvements à force centrale.

