Limaçon de Pascal

Le limaçon de Pascal est une courbe plane fermée présentant éventuellement un point double, obtenue en traçant le mouvement décrit par un point d'un disque roulant (sans glisser) sur un cercle. La cardioïde en est un cas particulier : le point double dégénère alors un rebroussement de première espèce. Le limaçon trisecteur est un second cas particulier (à ne pas confondre avec la trisectrice de Maclaurin)

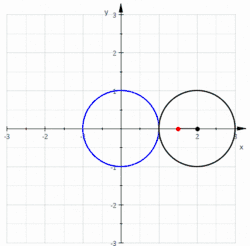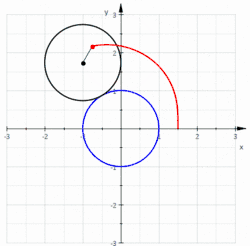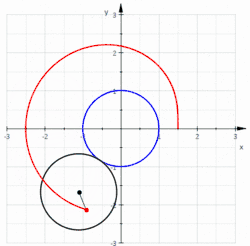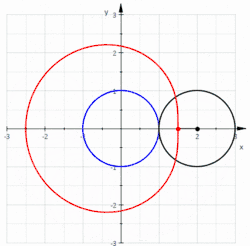
animation montrant la génération d'un limaçon par le mouvement d'un disque sur un cercle

Le limaçon est une épitrochoïde, c'est-à-dire une trochoïde avec un cercle pour base du mouvement.

Les limaçons de Pascal sont aussi les podaires d'un cercle par rapport à un point quelconque.

Étude sommaire

Le limaçon a pour équation en coordonnées polaires :

r=a+b\cos \theta ~

ce qui donne, en coordonnées cartésiennes :

(x^{2}+y^{2})^{2}-(a^{2}+2bx)(x^{2}+y^{2})+b^{2}x^{2}=0.~

C'est donc une quartique rationnelle, c'est-à-dire une courbe algébrique de degré 4.

Histoire

L'intérêt des Pascal pour les roulettes est bien documenté. Le limaçon, qui en est une généralisation, a été proposé comme sujet d'étude par Étienne Pascal, père de Blaise Pascal, au père Mersenne, d'où son nom. On retrouve toutefois déjà cette courbe dans l'Underweysung der Messung d'Albrecht Dürer, qui en indique le tracé avec des outils de dessin[1].

représentation graphique d'un limaçon, d'une cardioïde et de la trisectrice

De gauche à droite : un limaçon, une cardioïde et la trisectrice.

Notes et références

Dürer parle de ligne arachnéenne, par allusion à l'araignée d'un astrolabe : cf. Albrecht Dürer (trad. de l'allemand par Jeanne Peiffer), Géométrie [« Underweysung der Messung »], Paris, éditions du Seuil, 1995, 410 p. (ISBN 2-02-012427-0), p. 183

Voir aussi

Limaçon de Pascal sur MathCurve.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.