Coordonnées polaires
Les coordonnées polairescol. 2''s.v.''coordonnées_polaires_1-0">[1] sont, en mathématiques, un système de coordonnées curvilignescol. 1''s.v.''coordonnées_curvilignes_2-0">[2] à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une distance. Ce système est particulièrement utile dans les situations où la relation entre deux points est plus facile à exprimer en termes d’angle et de distance, comme dans le cas du pendule. Dans ce cas, le système des coordonnées cartésiennes, plus familier, impliquerait d’utiliser des formules trigonométriques pour exprimer une telle relation.
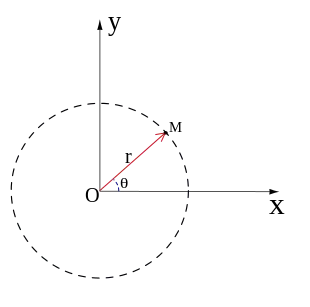

Comme il s’agit d’un système bidimensionnel, chaque point est déterminé par ses deux coordonnées polaires, la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (souvent notée r ou ρ, et appelée rayon) exprime la distance du point à un point central appelé pôle (équivalent à l’origine des coordonnées cartésiennes). La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée θ ou t) exprime la mesure, dans le sens trigonométrique (sens positif), de l’angle entre le point et la demi-droite d’angle 0°, appelée axe polaire[alpha 1].
Histoire
Le concept d’angle et de rayon était déjà utilisé lors du Ier millénaire av. J.-C. L’astronome Hipparque créa une table trigonométrique qui donnait la longueur de la corde pour chaque angle, et il utilisait les coordonnées polaires pour établir les positions des étoiles[3]. Dans Des spirales, Archimède étudia la spirale d'Archimède, dans laquelle le rayon est fonction de l’angle. Cependant les Grecs ne l’étendront pas à un système de coordonnées complet.
Il existe plusieurs versions de l’introduction des coordonnées polaires comme système de coordonnées formel. Grégoire de Saint-Vincent et Bonaventura Cavalieri ont indépendamment introduit ce concept dans le milieu du XVIIe siècle. Saint-Vincent a écrit sur ce thème en 1625 et a publié son travail en 1647, pendant que Cavalieri publia ses écrits en 1635, une version corrigée vit le jour en 1653. Cavalieri a d’abord utilisé les coordonnées polaires pour résoudre un problème relatif à l’aire sous une spirale d'Archimède. Blaise Pascal usait largement des coordonnées polaires pour calculer la longueur de paraboles.
Dans Méthode des Fluxions (écrit en 1671, publié en 1736), Isaac Newton étudia les transformations entre les coordonnées polaires, qu'il appelait "Seventh Manner; For Spirals", et neuf autres systèmes de coordonnées[4]. Dans le journal Acta Eruditorum (1691), Jacques Bernoulli utilisa un système avec un point et une droite, appelés respectivement le pôle et l'axe polaire. Les coordonnées étaient déterminées par leur distance au pôle et leur angle par rapport à l'axe polaire. Bernoulli utilisa même ce système pour déterminer le rayon de courbure de courbes exprimées dans ce système.
Le terme actuel de coordonnées polaires a été attribué à Gregorio Fontana et a été utilisé par les écrivains italiens du XIIIe siècle. Le terme apparait en anglais pour la première fois dans la traduction de 1816 effectuée par George Peacock du Traité du calcul différentiel et du calcul intégral de Sylvestre-François Lacroix[5] - [6]. Alexis Clairaut fut le premier à penser à étendre les coordonnées polaires en trois dimensions, et Leonhard Euler a été le premier à vraiment les développer[7].
Placer des points en coordonnées polaires
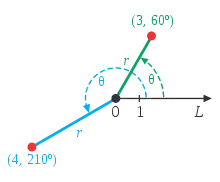
Chaque point du plan est déterminé par les coordonnées polaires, qui sont la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (souvent notée r ou ρ, et appelé rayon) exprime la distance du point à un point central appelé pôle (équivalent à l'origine des coordonnées cartésiennes). La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée t ou θ) exprime la mesure, dans le sens trigonométrique, de l’angle entre le point et la demi-droite d’angle 0°, appelé axe polaire (équivalent à l’axe des abscisses en coordonnées cartésiennes)[8].
Par exemple, le point de coordonnées polaires (3 ; 60°) sera placé à trois unités de distance du pôle sur la demi-droite d’angle 60°. Le point (–3 ; –120°) sera au même endroit car une distance négative sera considérée comme une mesure positive sur la demi-droite opposée par rapport au pôle (tournée de 180° par rapport à la demi-droite d’origine).
L’un des aspects importants du système de coordonnées polaires, qui n’est pas présent dans le système cartésien, est qu’il existe une infinité de coordonnées polaires désignant un même et unique point. En effet, on peut rajouter des mesures d’un tour complet sans affecter l’emplacement du point. Par exemple, le point (3 ; 420°) est confondu avec le point (3 ; 60°). En général, le point (r ; θ) peut être représenté par (r ; θ ± 2nπ) ou (−r ; θ ± (2 n + 1)π), où n est un entier quelconque et les angles sont notés en radians[9].
Les coordonnées arbitraires (0 ; θ) sont conventionnellement utilisées pour représenter le pôle, sans se soucier de la valeur attribuée dans ce cas à l’angle θ, un point de rayon r = 0 sera toujours sur le pôle[10]. Pour obtenir un unique représentant du point, on limite le rayon aux réels positifs et l’angle entre –180° et 180° (ou 0° et 360°), ou si l’on utilise les radians entre –π et π (ou 0 et 2π). On dit que l’angle est donné modulo 360° ou 2π[11].
L’angle en notation polaire est généralement donné en degrés ou radians, en utilisant la convention 2π = 360°. Le choix dépend du contexte. En navigation, les degrés sont de rigueur, alors que certaines applications physiques (comme l’étude des rotations en mécanique) et la plupart des mathématiques utilisent les radians[12].
Conversion entre système polaire et cartésien
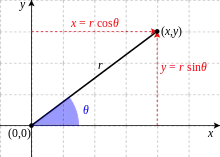
Les deux coordonnées polaires r et θ peuvent être converties en coordonnées cartésiennes x et y en utilisant les fonctions trigonométriques sinus et cosinus :
Deux coordonnées cartésiennes x et y permettent de calculer la première coordonnée polaire r par :
- (par une simple application du théorème de Pythagore).
Pour déterminer la seconde (l’angle θ), on doit distinguer deux cas :
- pour r = 0, l’angle peut prendre n’importe quelle valeur réelle ;
- pour r ≠ 0, pour obtenir une unique valeur de θ, on se restreint à l’intervalle [0, 2 π[ (ou de manière équivalente ]–π, π]).
Pour obtenir θ dans l’intervalle [0, 2π[, on utilise les formules suivantes (arctan désigne la réciproque de la fonction tangente) :
Pour l’obtenir dans l’intervalle ]–π, π], on utilise les formules[13] :
Pour obtenir θ dans l’intervalle ]–π, π[, on peut également utiliser la formule suivante, plus concise :
qui est valable pour tout point du plan à l'exception du demi-axe des abscisses négatives.
On peut aussi utiliser la fonction atan2 :
ou encore la fonction arccos ou arcsin : voir Nombre complexe#Coordonnées polaires.
Équation polaire
Une équation qui définit une courbe algébrique exprimée en coordonnées polaires est connue sous le nom d’équation polaire. Dans la plupart des cas, une telle équation peut être spécifiée en définissant r comme une fonction de θ. La courbe résultante est alors formée des points du type (r(θ) ; θ) et peut être vue comme le graphe de la fonction polaire r.
Différentes formes de symétries peuvent être déduites de l’équation d’une fonction polaire. Si r(–θ) = r(θ) alors la courbe est symétrique par rapport à l’axe horizontal (les demi-droites 0° et 180°). Si r(π – θ) = r(θ), la courbe sera symétrique par rapport à l’axe vertical (90° et 270°).
À cause du caractère circulaire des coordonnées polaires, beaucoup de courbes peuvent être décrites par une équation polaire simple, alors que leur équation cartésienne serait beaucoup plus compliquée. Quelques courbes polaires les plus connues sont : la spirale d'Archimède, la lemniscate de Bernoulli, le limaçon de Pascal ou encore la cardioïde.
Cercle

L'équation générale d'un cercle de centre (r0 ; φ) et de rayon a est :
Dans de nombreux cas, cette équation est simplifiée[14]. Par exemple,
- pour un cercle centré sur le pôle et de rayon a :
- pour un cercle passant par le pôle (r0 = a) :
Droite
- Une droite radiale (qui passe par le pôle) est représentée par l'équation :
- où φ, constant, correspond à l'angle de la droite. On a donc φ = arctan m où m est la pente de la droite en coordonnées cartésiennes.
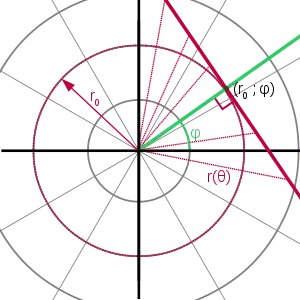
- Une droite non radiale qui coupe perpendiculairement au point (r0; φ) la droite radiale définie par son angle constant φ, de façon que la droite non radiale soit tangente d'un cercle hypothétique de rayon r0, a pour équation :
- ou selon un équivalent de la fonction trigonométrique sécante :
- avec φ, constant, et θ appartenant à .
Rosace
.svg.png.webp)
Une rosace est une courbe très connue qui ressemble à des pétales de fleurs, et qui peut être exprimée par une simple équation polaire :
pour n'importe quelle constante réelle φ0. Si k est un entier, cette équation produit une fleur avec 2k pétale(s) si k est pair, et k pétale(s) si k est impair. Si k est un nombre rationnel, l'équation produit une courbe en forme de fleur dont les pétales se chevauchent. Ces équations ne peuvent fournir de courbe en forme de fleur à 2, 6, 10, 14… pétales. La constante réelle a détermine la longueur d'un pétale du centre à son extrémité.
Spirale d'Archimède
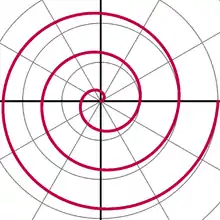
La spirale d'Archimède est une spirale découverte par Archimède, qui peut être également exprimée à partir d'une équation polaire :
Changer le paramètre a fait tourner la spirale autour du pôle, alors que b détermine la distance entre les bras, qui pour une spirale donnée est constante. Une spirale d'Archimède possède deux bras, connectés au pôle : l'un pour θ ≥ 0 et l'autre pour θ ≤ 0, lorsque a = 0, et alors chaque bras est le symétrique de l'autre par rapport à l'axe vertical (90°/270°). Cette courbe est l'une des premières courbe, après les coniques, à être décrite par des termes mathématiques et à être un exemple de courbe simplement exprimée en coordonnées polaires.
Conique
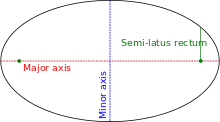
Une conique avec un foyer confondu avec le pôle et un autre sur l'axe polaire (0°), le grand axe étant confondu avec l'axe polaire) est donnée par l'équation :
où e est l'excentricité et p est appelé paramètre de la conique, et correspond à la longueur du segment perpendiculaire au grand axe joignant le foyer à la courbe. Si e > 1 l'équation définit une hyperbole, si e = 1, une parabole, si e < 1 une ellipse. Enfin pour e = 0 on obtient un cercle de rayon p.
Nombre complexe
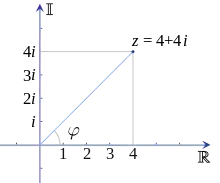
Chaque nombre complexe peut être représenté par un point dans le plan complexe, et de plus peut être exprimé par ses coordonnées cartésiennes (appelé forme algébrique du nombre complexe) ou par ses coordonnées polaires. La forme algébrique d'un nombre complexe z est de la forme :
où x et y sont des réels et i est l'unité imaginaire. Sa forme polaire est (d'après les formules données plus haut) :
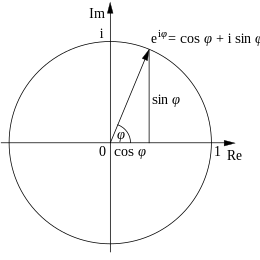
où r est un réel positif ou nul (r étant nul si et seulement z est nul) et θ un réel. De là on en déduit :
ce qui est équivalent, par la formule d'Euler[15] (à noter que toutes ces formules, à l'instar de toutes les autres utilisant l'exponentielle ou les angles, utilisent les radians). Pour convertir d'une forme à l'autre, les formules données plus haut conviennent).
L'addition de nombres complexes est plus aisée en forme algébrique mais la multiplication, la division et l'exponentiation sont plus faciles à réaliser en forme exponentielle (ou de manière équivalente en forme polaire) :
- Multiplication :
- Division :
- Exponentiation (formule de Moivre) avec n entier :
Calcul infinitésimal
Le calcul infinitésimal peut être appliqué aux équations exprimées en coordonnées polaires. La coordonnée angulaire θ est exprimée en radian, qui est le choix naturel en analyse[16] - [17].
Calcul différentiel et changement de variables polaire
La matrice jacobienne du changement de variable polaire s'écrit
- ,
ce qu'on écrit également sous la forme suivante :
- ;
- .
Les dérivées secondes s'expriment également au travers d'une matrice.
Les opérateurs homogènes
s'obtiennent matriciellement par :
- ,
où l'on a noté, pour alléger l'expression, c en lieu et place de cosθ et s pour sinθ.
On dispose d'ailleurs du même type de changement de dérivées successives au travers de matrices pour tous les ordres de dérivation.
Calcul différentiel et courbe en coordonnées polaires
Pour trouver la pente cartésienne de la tangente à la courbe polaire r(θ) à un point donné, la courbe doit d'abord être exprimée en un système paramétrique :
- .
Puis on différentie les deux équations :
- .
En divisant la deuxième équation par la première, on obtient la pente cartésienne de la tangente à la courbe polaire au point (r(θ) ; θ) :
- .
Ainsi, au point (r(θ) ; θ), l'angle γ entre l'axe Ox et la tangente à la courbe est donné par la relation :
- .
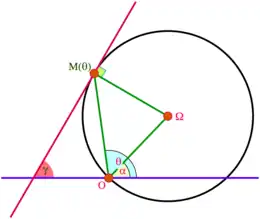
Dans le cas d'un cercle passant par l'origine, de centre Ω = (r0 ; α) et de rayon r0, d'équation :
- ,
la formule donnant γ (voir figure ci-contre) conduit à
- ,
ce qui démontre au passage le théorème de l'angle inscrit et de l'angle au centre.
Calcul intégral
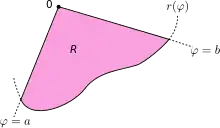
Soit R une surface du plan délimitée par la courbe continue r(θ) et les demi-droites θ = a et θ = b, où 0 < b − a < 2π (a et b étant des réels). Alors l'aire S de cette surface est
- .
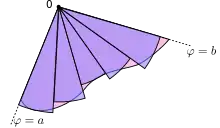
Le résultat peut être retrouvé par le raisonnement suivant. Tout d'abord, l'intervalle [a, b] est subdivisé en n sous-intervalles, où n est un entier positif quelconque. Alors Δθ, la longueur de chaque sous-intervalle, est égal à b – a divisé par n, le nombre de sous-intervalles. Pour chaque sous-intervalle i = 1, 2, ..., n, soit θi le milieu de chaque sous-intervalle i. On peut alors construire un secteur circulaire où le centre est le pôle, de rayon r(θi), d'angle Δθ et de longueur d'arc r(θi) Δθ. L'aire Si de chaque secteur est donc
et donc l'aire totale de tous les secteurs est :
- .
Pour n tendant vers l'infini, l'approximation devient meilleure et cette somme est une somme de Riemann et donc converge vers l'intégrale demandée :
- .
Généralisation
En utilisant les coordonnées cartésiennes, un élément d'aire infinitésimale peut être calculé comme dA = dx dy. La règle du changement de variable pour des intégrales multiples stipule que, lorsque l'on utilise d'autres systèmes de coordonnées, le Jacobien de la matrice de conversion des coordonnées est:
- .
Un élément d'aire infinitésimale peut donc être vu comme
- .
Maintenant une fonction donnée en coordonnées polaires peut être intégrée comme ceci
- .
Ici R est la même surface que plus haut, c'est-à-dire la surface comprise entre la courbe r(θ) et les demi-droites θ = a et θ = b.
La formule pour l'aire de R mentionnée plus haut est retrouvée en prenant f la fonction constante égale à 1. L'une des applications de ces formules est le calcul de l'intégrale de Gauss .
Analyse vectorielle
L'analyse vectorielle peut être également appliquée aux coordonnées polaires. Soit le vecteur position , avec r et θ dépendants du temps t, et soit un vecteur unitaire de même direction que et un vecteur unitaire orthogonal à . Les dérivées première et seconde du vecteur position sont données par :
- ;
- .
Trois dimensions
Le système de coordonnées polaires peut être étendu à l'espace usuel à trois dimensions de deux manières, ce qui donne le système de coordonnées cylindriques et le système de coordonnées sphériques. Le concept des coordonnées cylindriques est de rajouter une coordonnée de distance, alors que le système sphérique rajoute une coordonnée angulaire.
Coordonnées cylindriques
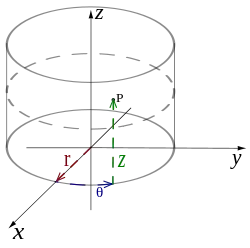
Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui mesure la hauteur d'un point par rapport au plan repéré par les coordonnées polaires ; de la même manière que l'on étend le système de coordonnées cartésiennes de deux à trois dimensions. La troisième coordonnée est souvent notée h ou z. La notation r étant systématiquement utilisée en coordonnées sphériques (voir ci-dessous), on lui préfère ici la lettre grecque ρ.
Les trois coordonnées cylindriques peuvent être converties en coordonnées cartésiennes par :
Coordonnées sphériques
.svg.png.webp)
Les coordonnées polaires peuvent aussi être étendues à l'espace tridimensionnel euclidien, suivant diverses conventions de notation.
En physique, on utilise le plus souvent les coordonnées (r, θ, φ), où r désigne la distance du point au pôle, θ est l'angle depuis l'axe des z (appelé colatitude ou zénith, compris entre 0° et 180°) et φ est l'angle depuis l'axe des x (comme dans les coordonnées polaires, entre 0° et 360°).
En mathématiques, en nommant les coordonnées (ρ, θ, φ), où ρ désigne toujours la distance du point au pôle, alors que θ désigne cette fois la longitude (angle mesuré depuis l'axe des x et compris entre –180° et 180°) et φ la latitude, l'angle depuis le plan équatorial (entre –90° et 90°).
Un système mixte consiste à utiliser dans l'ordre, le rayon, la longitude et ensuite la colatitude, notés toujours (ρ, θ, φ).
Ces trois systèmes de coordonnées sont des exemples de coordonnées sphériques et ils sont similaires au système utilisé pour se repérer sur la surface de la Terre. Ils ont chacun leur utilité propre mais il faut prendre garde qu'en physique, on nomme θ la colatitude alors qu'en mathématiques, on nomme généralement θ la longitude. La latitude (φ en mathématiques) et la colatitude (θ en physique) étant complémentaires l'une de l'autre[18], il est aisé de passer d'un système à un autre.
.svg.png.webp)
Les trois coordonnées sphériques peuvent être converties en coordonnées cartésiennes par :
dans le système rayon-colatitude-longitude (physique), et
dans le système rayon-longitude-latitude (mathématiques).
Applications
Les coordonnées polaires sont bidimensionnelles et peuvent donc être uniquement utilisées dans les cas où les points sont dans un même plan. Elles sont plus appropriées dans tous les cas où le phénomène considéré est lié à une direction et une longueur d'un point central. Par exemple, les exemples de courbes polaires définies plus haut montrent comment on peut utiliser les coordonnées polaires pour produire des équations simples produisant ces courbes, comme la spirale d'Archimède. Ces mêmes équations en coordonnées cartésiennes seraient beaucoup plus compliquées. De plus, beaucoup d'études de systèmes physiques, comme l'étude du pendule ou bien tout phénomène où des solides se meuvent autour d'un point central, sont simplifiées en passant en coordonnées polaires. L'introduction des coordonnées polaires s'est faite tout d'abord pour étudier les mouvements circulaires et les mouvements orbitaux.
Navigation
Les coordonnées polaires sont souvent utilisées en navigation. En effet, un voyage peut être défini par une distance et un angle par rapport à la destination. Par exemple, les aéronefs utilisent un système de coordonnées polaires quelque peu modifié pour la navigation.
Modélisation
Les coordonnées polaires conduisent à une simplification du modèle des systèmes naturels dans lequel un point central joue un rôle particulier. C'est notamment le cas des systèmes possédant une symétrie de rotation, c'est-à-dire ceux qui sont invariants par rotation autour d'un point fixe.
C'est le cas des systèmes dits à force centrale, c'est-à-dire soumis à une force qui passe par un point fixe. Les exemples classiques comprennent le problème à deux corps (en gravitation ou en électromagnétisme) et plus généralement dans l'étude du mouvement des planètes[19], ainsi que les systèmes possédant une source ponctuelle (en), comme les antennes radioélectriques.
C'est aussi le cas des mouvements de rotation autour d'un point fixe comme le pendule simple, des surfaces d'équilibres autour d'un puits comme l'équation de flux d'eau du sol ou de la variation d'une grandeur en fonction d'un angle comme les polaires en aéronautique ou la directivité d'un microphone, qui caractérise la sensibilité du microphone en fonction de la provenance du son selon l'axe central du microphone.
Ce phénomène peut être représenté par une courbe polaire. La courbe pour un microphone cardioïde standard, le plus commun des microphones, a pour équation r = (1 + sin θ)/2[20].
Enfin, il existe des cas particuliers où le passage aux coordonnées polaires peut rendre service. Par exemple, la loi de Laplace-Gauss en statistique a une distribution qui n'est intégrable au moyen de fonctions élémentaires. Toutefois, en faisant tourner cette courbe autour de l'axe des y on obtient une cloche infinie qui, exprimée en coordonnées polaires, est intégrable. C'est de cette façon que Gauss a pu normaliser cette loi statistique dont Laplace avait montré l'universalité.
Notes et références
Notes
- Dans certains cas, notamment celui de courbes s'enroulant plusieurs fois autour de l'origine, il peut être commode de supprimer la restriction ( et ) et d’utiliser les coordonnées équivalentes ou , où n est un entier quelconque.
Références
- col. 2''s.v.''coordonnées_polaires-1" class="mw-reference-text">Taillet, Villain et Febvre 2018, s.v.coordonnées polaires, p. 160, col. 2.
- col. 1''s.v.''coordonnées_curvilignes-2" class="mw-reference-text">Taillet, Villain et Febvre 2018, s.v.coordonnées curvilignes, p. 159, col. 1.
- (en) Michael Friendly et Daniel J. Denis, « Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization ».
- (en) C. B. Boyer, « Newton as an Originator of Polar Coordinates », American Mathematical Monthly, vol. 56, , p. 73-78 (JSTOR 2306162).
- (en) Jeff Miller, « Earliest Known Uses of Some of the Words of Mathematics ».
- (en) David Eugene Smith, History of Mathematics, vol. 2, Boston, Ginn and Co., , p. 324.
- (en) Julian Coolidge, « The Origin of Polar Coordinates », Amer. Math. Monthly, vol. 59, , p. 78-85 (JSTOR 2307104, résumé).
- (en) Richard G. Brown et Andrew M. Gleason, Advanced Mathematics : Precalculus with Discrete Mathematics and Data Analysis, Evanston, Illinois, McDougal Littell, (ISBN 0-395-77114-5).
- (en) « Polar Coordinates and Graphing », sur fortbendisd.com, .
- (en) Theodore Lee, David Cohen et David Sklar, Precalculus : With Unit-Circle Trigonometry, Thomson Brooks/Cole, , 4e éd. (ISBN 0-534-40230-5).
- (en) Ian Stewart et David Tall, Complex Analysis (the Hitchhiker's Guide to the Plane), CUP, , 290 p. (ISBN 0-521-28763-4, lire en ligne).
- (en) Raymond A. Serway et John W. Jewett Jr., Principles of Physics : A Calculus-Based Text, Brooks/Cole—Thomson Learning, , 1150 p. (ISBN 0-534-49143-X).
- (en) Bruce Follett Torrence et Eve Torrence, The Student's Introduction to Mathematica, CUP, (ISBN 0-521-59461-8).
- (en) Johan Claeys, « Polar coordinates », sur ping.be.
- (en) Julius O. Smith, Mathematics of the Discrete Fourier Transform (DFT), W3K Publishing, , 2e éd. (1re éd. 2003), 306 p. (ISBN 978-0-9745607-4-8, lire en ligne), « Euler's Identity ».
- (en) Lawrence S. Husch, « Areas Bounded by Polar Curves », sur archives.math.utk.edu.
- (en) Lawrence S. Husch, « Tangent Lines to Polar Graphs », sur archives.math.utk.edu.
- (en) Frank Wattenberg, « Spherical Coordinates », sur math.montana.edu, .
- Jacques Dixmier, Cours de mathématiques du premier cycle, première année, Gauthier-Villars, (ISBN 2040157735), p. 453.
- (en) John Eargle, Handbook of Recording Engineering, Springer, , 4e éd., 436 p. (ISBN 0-387-28470-2, lire en ligne).
Voir aussi
Articles connexes
- Harmonique sphérique
- Les angles d'Euler, une généralisation des coordonnées sphériques.
Lien externe
(en) spherical.pdf Une proposition pour unifier les notations polaires 2D et 3D.
Bibliographie
- (en) Howard Anton, Irl Bivens et Stephen Davis, Calculus, Single Variable, John Wiley & Sons, , 10e éd., 880 p. (ISBN 978-0-470-64770-7, lire en ligne), p. 705-719
- (en) Ross Finney, George B. Thomas (en), Franklin Demana et Bert Waits, Calculus : Graphical, Numerical, Algebraic : Single Variable Version, Addison-Wesley, , 1104 p. (ISBN 978-0-201-55478-6)
- [Taillet, Villain et Febvre 2018] R. Taillet, L. Villain et P. Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Sup., hors coll., , 4e éd. (1re éd. ), 1 vol., X-956, ill. et fig., 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne), s.v.coordonnées polaires, p. 160, col. 2.


![{\displaystyle \theta ={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{si }}x>0{\mbox{ et }}y\geq 0,\\[3pt]\arctan({\frac {y}{x}})+2\pi &{\mbox{si }}x>0{\mbox{ et }}y<0,\\[3pt]\arctan({\frac {y}{x}})+\pi &{\mbox{si }}x<0,\\[3pt]{\frac {\pi }{2}}&{\mbox{si }}x=0{\mbox{ et }}y>0,\\[3pt]{\frac {3\pi }{2}}&{\mbox{si }}x=0{\mbox{ et }}y<0.\end{cases}}}](https://img.franco.wiki/i/fbd4d482600eac8c9ddcccb9fb2c209cfd71eb7d.svg)
![{\displaystyle \theta ={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{si }}x>0,\\[3pt]\arctan({\frac {y}{x}})+\pi &{\mbox{si }}x<0{\mbox{ et }}y\geq 0,\\[3pt]\arctan({\frac {y}{x}})-\pi &{\mbox{si }}x<0{\mbox{ et }}y<0,\\[3pt]{\frac {\pi }{2}}&{\mbox{si }}x=0{\mbox{ et }}y>0,\\[3pt]-{\frac {\pi }{2}}&{\mbox{si }}x=0{\mbox{ et }}y<0.\end{cases}}}](https://img.franco.wiki/i/e526e174429255b93b5b8ddbd57ca30cc10adba1.svg)























































