Origine (mathématiques)
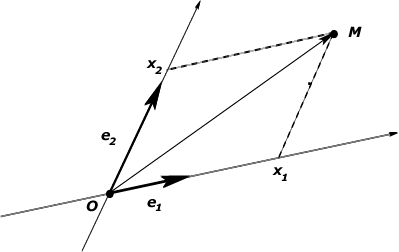
En mathématiques, l'origine d'un espace euclidien est un point spécial, couramment noté O, utilisé comme point fixe de référence qui servira de repère pour la géométrie de l'espace environnant.
|
Dans les problèmes physiques, le choix de l'origine est souvent arbitraire, ce qui impliquerait que le choix de n'importe quelle origine donnera la même réponse. Ceci autorise à choisir un point d'origine qui simplifie les calculs autant que possible, en utilisant notamment des propriétés avantageuses de symétrie.
Coordonnées cartésiennes
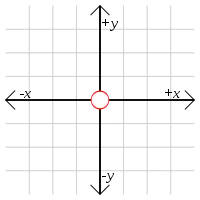
Dans un système de coordonnées cartésiennes, l'origine est le point où les deux axes du repère se croisent[1]. L'origine divise chaque axe en deux parties, un demi-axe positif et un négatif[2]. Les points sont alors repérés depuis l'origine par leurs coordonnées numériques, soient les positions des projections orthogonales sur chacun des axes. Les coordonnées de l'origine sont donc toujours nulles, soit (0;0) dans le plan et (0;0;0) dans l'espace[1].
Autres systèmes de coordonnées
Dans un système de coordonnées polaires, l'origine est aussi parfois appelée pôle. Elle n'a pas de coordonnées polaires bien définies, car les coordonnées polaires utilisent un angle formé par rapport à l'axe des abscisses et le rayon entre l'origine au point, qu'il est impossible de définir quand ce rayon est réduit à un point[3].
En géométrie euclidienne, l'origine peut être choisie librement comme tout point de référence avantageux[4]
L'origine du plan complexe peut être défini comme le point où l'axe réel et l'axe imaginaire se rencontrent, ce qui correspond au nombre complexe nul[5].
Voir aussi
- Vecteur nul, un analogue dans un espace vectoriel
- Distance d'un point à un plan
- Espace pointé, un espace topologique avec un point distingué
- Fonction de base radiale, une fonction qui ne dépend que de la distance à l'origine
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Origin (mathematics) » (voir la liste des auteurs).
- (en) David A. Madsen, Engineering Drawing and Design, Thompson Learning, coll. « Delmar drafting series », (ISBN 9780766816343, lire en ligne), p. 120.
- (en) Lev S. Pontrjagin, Learning higher mathematics, Springer-Verlag, coll. « Springer series in Soviet mathematics », (ISBN 9783540123514), p. 73.
- (en) James Stuart Tanton, Encyclopedia of Mathematics, Infobase Publishing, (ISBN 9780816051243, lire en ligne).
- (en) John M. Lee, Axiomatic Geometry, vol. 21, American Mathematical Society, coll. « Pure and Applied Undergraduate Texts », (ISBN 9780821884782, lire en ligne), p. 134.
- (en) Mario Gonzalez, Classical Complex Analysis, CRC Press, coll. « Chapman & Hall Pure and Applied Mathematics », (ISBN 9780824784157).