Fonction de base radiale

Une fonction ${\displaystyle \phi$ :\mathbb {R} ^{d}\rightarrow \mathbb {R} } est dite radiale s'il existe une fonction ${\displaystyle \varphi$ :[0,\infty [\rightarrow \mathbb {R} } telle que: ${\displaystyle \phi (x)=\varphi (r)}$ avec ${\displaystyle r=\lVert x\rVert }$ et ${\displaystyle \lVert \cdot \rVert }$ une norme définie sur ${\displaystyle \mathbb {R} ^{d}}$ - généralement la norme euclidienne. De plus, une fonction radiale est toujours symétrique par rapport à son centre (ou origine), en d'autres termes, ${\displaystyle \lVert x_{1}\rVert =\lVert x_{2}\rVert \implies \phi (x_{1})=\phi (x_{2})}$ avec ${\displaystyle x_{1},x_{2}\in \mathbb {R} ^{d}}$. Une fonction radiale centrée en un point ${\displaystyle c}$ s'écrit donc sous la forme ${\displaystyle \phi _{c}(x)=\varphi (\lVert x-c\rVert )}$.

Gaussienne pour différents choix de ${\displaystyle \epsilon }$

Multiquadratique pour différents choix de ${\displaystyle \epsilon }$

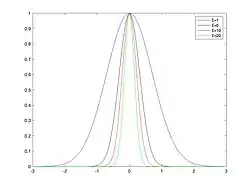
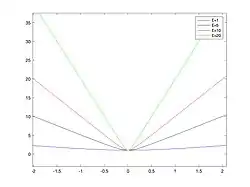
En posant ${\displaystyle r=\lVert x-c\rVert }$ et ${\displaystyle \epsilon }$ le paramètre de forme qui a une influence sur la forme que prend la courbe de la fonction, il existe plusieurs fonctions de base radiale connues à ce jour, les plus courantes sont :

• Gaussienne :

${\displaystyle \varphi (r)=e^{-{(\epsilon r)}^{2}}}$,

• Multiquadratique :

${\displaystyle \varphi (r)={\sqrt {1+{(\epsilon r)}^{2}}}}$,

• Multiquadratique inverse :

${\displaystyle \varphi (r)={\sqrt {\frac {1}{1+{(\epsilon r)}^{2}}}}}$,

• Quadratique inverse :

${\displaystyle \varphi (r)={\frac {1}{1+{(\epsilon r)}^{2}}}}$,

• Spline polyharmonique :

${\displaystyle {\begin{aligned}\varphi (r)&=r^{k},&\ \mathrm {pour} \ k&=1,3,5,\dotsc \\\varphi (r)&=r^{k}\ln(r),&\ \mathrm {pour} \ k&=2,4,6,\dotsc \end{aligned}}}$

• Spline en plaque mince

${\displaystyle \varphi (r)=r^{2}\ln(r),}$

• Fonction à support compact

Cette famille de fonctions sont non nulles uniquement dans un rayon de 1/ϵ autour de l'origine

• • Fonction test :

${\displaystyle \varphi (r)=\exp \left(-{\frac {1}{1-(\varepsilon r)^{2}}}\right)1\!\!1_{]-{\frac {1}{\varepsilon }},{\frac {1}{\varepsilon }}[}}$

Une petite valeur du paramètre fait que la fonction devienne plate. En revanche, une grande valeur du paramètre se traduit par une forme plus pointue de la courbe. De plus, ces fonctions sont de classe ${\displaystyle C^{\infty }(\mathbb {R} )}$, donc indéfiniment différentiables et définies positives.

Les fonctions de base radiale sont utilisées pour construire des approximation de fonctions de la forme

${\displaystyle f(\mathbf {x} )=\sum _{i=1}^{N}w_{i}\,\varphi (\left\|\mathbf {x} -\mathbf {x} _{i}\right\|),}$

qui est donc représentée comme une somme pondérée de N fonctions de base radiale, chacune associé à un centre différent x_i, et pondérée par un coefficient adapté w_i. Les poids peuvent être estimés par moindres carrés linéaires, car la fonction approchante dépend linéairement des poids.

Des approximation de ce type ont été utilisées pour des prédictions de séries temporelles et théorie du contrôle de systèmes non linéaires montrant des comportements chaotiques assez simples ou de la reconstitution 3D en imagerie numérique (par RBF hiérarchique et déformation de pose spatiale).

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Radial basis function » (voir la liste des auteurs).
• R.L. Hardy, « Multiquadric equations of topography and other irregular surfaces », Journal of Geophysical Research, vol. 76, n^o 8,‎ 1971, p. 1905–1915 (DOI 10.1029/jb076i008p01905, Bibcode 1971JGR....76.1905H)
• R.L. Hardy, « Theory and applications of the multiquadric-biharmonic method, 20 years of Discovery, 1968 1988 », Comp. Math Applic, vol. 19, n^os 8/9,‎ 1990, p. 163–208 (DOI 10.1016/0898-1221(90)90272-l )
• WH Press, SA Teukolsky, WT Vetterling et BP Flannery, Numerical Recipes: The Art of Scientific Computing, New York, Cambridge University Press, 2007 (ISBN 978-0-521-88068-8), « Section 3.7.1. Radial Basis Function Interpolation »
• Sirayanone, S., 1988, Comparative studies of kriging, multiquadric-biharmonic, and other methods for solving mineral resource problems, PhD. Dissertation, Dept. of Earth Sciences, Iowa State University, Ames, Iowa.
• S. Sirayanone et R.L. Hardy, « The Multiquadric-biharmonic Method as Used for Mineral Resources, Meteorological, and Other Applications », Journal of Applied Sciences and Computations, vol. 1,‎ 1995, p. 437–475