Cubique de Tschirnhausen
En géométrie, la cubique de Tschirnhausen est une courbe algébrique définie par l'équation polaire

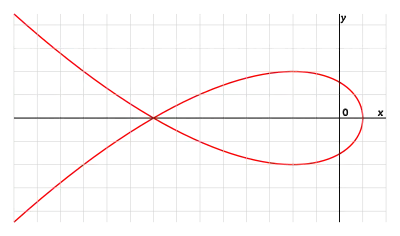
Cubique de Tschirnhausen, pour a=1
(sec est la fonction sécante, inverse du cosinus)
Histoire
Cette courbe fut étudiée par Ehrenfried Walther von Tschirnhaus, Guillaume de l'Hôpital et Eugène Catalan. Le nom de « cubique de Tschirnhausen » fut mentionné pour la première fois en 1900 par Raymond Clare Archibald, bien qu'elle soit parfois connue sous le nom de « cubique de L'Hôpital » ou « trisectrice de Catalan ».
Autres équations
Posons t = tan(θ/3). Selon la formule de De Moivre, cela donne :
![{\displaystyle x=a\cos(\theta )\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[\cos ^{3}\left({\frac {\theta }{3}}\right)-3\cos \left({\frac {\theta }{3}}\right)\sin ^{2}\left({\frac {\theta }{3}}\right)\right]\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[1-3\tan ^{2}\left({\frac {\theta }{3}}\right)\right]=a(1-3t^{2}),}](https://img.franco.wiki/i/8c78d425f87ac9e1a5b902b529b8bc9628046866.svg)
![{\displaystyle y=a\sin(\theta )\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[3\cos ^{2}\left({\frac {\theta }{3}}\right)\sin \left({\frac {\theta }{3}}\right)-\sin ^{3}\left({\frac {\theta }{3}}\right)\right]\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[3\tan \left({\frac {\theta }{3}}\right)-\tan ^{3}\left({\frac {\theta }{3}}\right)\right]=at(3-t^{2}).}](https://img.franco.wiki/i/9e810e64889f4c5d96bbc2b3274ea93736f9a47b.svg)
ce qui donne une équation paramétrique. Le paramètre t peut être facilement éliminé, ce qui donne l'équation cartésienne
 .
.
Si la courbe est translatée horizontalement de 8a, les équations deviennent

ou
 ,
,
ce qui donne la forme polaire
 .
.
Propriétés
Caustique
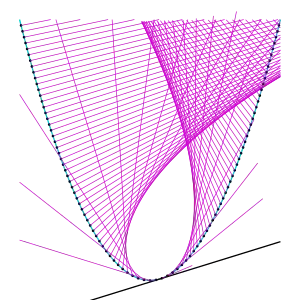
Caustique de parabole. Seuls les rayons réfléchis sont représentés. La direction des rayons incidents (non représentés) est donnée par celle de la tangente commune à la parabole et à la caustique, en noir. Les rayons réfléchis sur la gauche de la parabole proviennent d'une source à l'infini vers la droite, ceux réfléchis sur la droite de la parabole proviennent d'une source à l'infini vers la gauche.
Les caustiques de parabole, lorsque la source lumineuse est à l'infini, sont des cubiques de Tschirnhausen. Elle est réduite à un point, le foyer de la parabole, lorsque la direction de la source est l'axe de la parabole.
Voir aussi
Articles connexes
Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.



![{\displaystyle x=a\cos(\theta )\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[\cos ^{3}\left({\frac {\theta }{3}}\right)-3\cos \left({\frac {\theta }{3}}\right)\sin ^{2}\left({\frac {\theta }{3}}\right)\right]\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[1-3\tan ^{2}\left({\frac {\theta }{3}}\right)\right]=a(1-3t^{2}),}](https://img.franco.wiki/i/8c78d425f87ac9e1a5b902b529b8bc9628046866.svg)
![{\displaystyle y=a\sin(\theta )\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[3\cos ^{2}\left({\frac {\theta }{3}}\right)\sin \left({\frac {\theta }{3}}\right)-\sin ^{3}\left({\frac {\theta }{3}}\right)\right]\sec ^{3}\left({\frac {\theta }{3}}\right)=a\left[3\tan \left({\frac {\theta }{3}}\right)-\tan ^{3}\left({\frac {\theta }{3}}\right)\right]=at(3-t^{2}).}](https://img.franco.wiki/i/9e810e64889f4c5d96bbc2b3274ea93736f9a47b.svg)



